一種基于熱物性參數分布計算的連鑄坯熱跟蹤計算方法與流程

本發明涉及一種在線跟蹤模型的計算方法，具體涉及一種基于熱物性參數分布計算的連鑄坯熱跟蹤計算方法。

背景技術：

連鑄坯凝固末端的輕壓下技術和重壓下技術是有效改善鑄坯中心偏析和中心疏松問題的主要手段，而輕壓下和重壓下實施的前提條件是對凝固末端位置的準確預測。目前用來確定凝固末端位置的方法主要包括在線熱跟蹤模型計算、射釘法、凝固末端壓力反饋檢測法和目前尚在研究中的電磁超聲檢測法。而國內大多數企業受困于設備的條件限制，通常采用在線熱跟蹤模型的計算來預測凝固位置。

在線熱跟蹤模型中的物性參數計算的準確性直接影響到計算結果的準確性甚至計算過程的收斂性。其中物性參數主要包含：相分率、導熱系數、比熱容和密度等。一般的在線熱跟蹤模型中對固相率的計算通常采用clynetw等人提出的固相率隨溫度變化關系式：而導熱系數通常簡化為固定值，一般為33w/(kg·℃)。密度通常也采取固定值，即在液相區內取7000kg/m³，兩相區內取7200kg/m³，在固相區內取7600kg/m³。比熱容也通常選取固定值進行計算，固相比熱cs＝669.44j/(kg·℃)、兩相區比熱cm＝772j/(kg·℃)和液相比熱cl＝824.64j/(kg·℃)進行計算。這種選取的方式雖然簡單實用，而且某些參數可能具有一定的準確度，但是卻無法正確反映物性參數隨溫度變化的連續性。

也有學者提出了采用全耦合模型，即微觀溶質偏析與宏觀傳熱耦合計算的方法準確計算溫度場，全耦合模型的計算步驟如下：

第一步：首先采用切片法將鑄坯沿拉坯方向的橫截面劃分為單元網格，對于整個切片可結合邊界條件采用二維宏觀凝固傳熱方法，如有限元方法、有限差分方法等計算鑄坯的凝固傳熱，在一個計算周期內，通過宏觀凝固傳熱模型，可得到各節點的溫度、冷速等信息；

第二步：在一個計算周期內，根據各節點的溫度、冷速等信息，對每個節點位置都進行微觀溶質偏析計算，計算出該節點位置處的溶質偏析分布與相分率，并根據相分率計算得到導熱系數、比熱容、密度等宏觀凝固傳熱所需要的熱物性參數；

第三步：將各節點熱物性參數帶入下一個宏觀凝固傳熱計算周期，即步驟一，完成循環計算。

由于鑄坯節點數量較多，一般都大于10000個，因此在每個計算周期內都需要進行10000次以上的微觀溶質偏析計算；另一方面，為了保證宏、微觀模型在時間尺度上的一致性，一般計算周期都設為0.01s，而澆鑄歷程一般都大于30分鐘，因此整澆鑄歷程內需要完成180000次宏微觀耦合計算。顯然，在如此巨大的計算量下，是不可能實現在線計算的。

因此，目前的在線熱跟蹤模型：(1)大部分是無法考慮熱物性參數計算的，即使考慮了熱物性參數，也不能考慮鑄坯凝固過程中因碳、硅、錳、磷、硫元素溶質偏析分布不同所導致的物性參數差異性；(2)在板坯連鑄生產過程中只能考慮中心線上的熱跟蹤，無法預測鑄坯寬向的非均勻凝固特性，即寬向1/2/位置、1/4位置與1/8位置的坯殼生長速度差異性。

鑒于上述缺點，本發明提供了一種能夠考慮因溶質偏析分布不同而導致熱物性參數差異，且能預測鑄坯非均勻凝固規律的在線熱跟蹤計算方法。

技術實現要素：

為了克服上述現有技術存在的不足，本發明提供了一種基于熱物性參數分布計算的連鑄坯熱跟蹤計算方法。

為了實現上述目的，本發明提供如下技術方案：

一種基于熱物性參數分布計算的連鑄坯熱跟蹤計算方法，包括獲取離線數據和建立鑄坯寬向1/2位置在線熱跟蹤計算模型；

獲取離線數據包括以下內容：

離線計算鋼的熱物性參數：采用微觀凝固模型計算不同元素偏析程度條件下鋼的相分率，基于所述相分率計算鋼的熱物性參數，所述熱物性參數包括導熱系數、密度和比熱容，并將所述熱物性參數存儲在數據庫中；

離線獲取鑄坯寬向1/2位置處的凝固坯殼生長規律：利用宏觀偏析檢測獲取鑄坯寬向1/2位置處沿厚度方向上的鑄坯偏析分布規律，形成鋼中元素在鑄坯寬向1/2位置處“鑄坯厚度位置-元素偏析程度”的凝固坯殼生長規律并存儲在數據庫中；

離線獲取鑄坯寬向不同位置處凝固坯殼生長規律關系：根據二維宏觀凝固傳熱與微觀溶質偏析全耦合計算模型獲取鑄坯寬向1/8位置、1/4位置與寬向1/2位置鑄坯凝固坯殼生長規律關系并存儲在數據庫中；

建立鑄坯寬向1/2位置在線熱跟蹤計算模型，包括以下步驟：

獲取并讀入鑄坯初始澆鑄條件與澆鑄過程信息：包括鑄坯尺寸、鋼成分、拉速、過熱度、結晶器長度及冷卻量、結晶器進出口水溫差、二冷區劃分及各區實時水量；

生成跟蹤單元：在一個周期內，在結晶器彎月面位置生成一個新跟蹤單元，該跟蹤單元的凝固傳熱計算區間為鑄坯寬向1/2位置上沿厚度方向的凝固傳熱，并對所述跟蹤單元進行溫度和位置的初始化；

具體的，采用切片法生成跟蹤單元，切片法是指將整個鑄坯流線沿拉坯方向劃分為許多個跟蹤單元，認為流線由不斷“出生”的跟蹤單元所組成。將跟蹤單元的“坯齡”、初始溫度、位置、所處冷卻區、受水量等初始條件和過程條件與單元的溫度場相關聯，從而使跟蹤單元與時間相關，從靜態轉向動態。每個跟蹤單元表示流線拉坯方向上一個切面的溫度分布，所有跟蹤單元聯動起來就可以描述一個動態的溫度場；

選取熱物性參數：在一個跟蹤單元內，調用所述鑄坯初始澆鑄條件與澆鑄過程信息確定鑄坯厚度位置，在數據庫中選擇該厚度位置對應的元素偏析程度，并根據所述元素偏析程度調用數據庫中該位置對應的熱物性參數；

跟蹤單元求解計算：在一個周期內，調用所述熱物性參數，從結晶器液面開始對鑄坯寬向1/2位置的整個連鑄流長中的所有跟蹤單元完成一次溫度場計算；

非均勻凝固前沿計算：通過已獲取的所述鑄坯寬向1/2位置處的凝固坯殼生長規律和所述鑄坯寬向1/8位置、1/4位置與寬向1/2位置鑄坯凝固坯殼生長規律關系，獲取鑄坯寬向1/4與1/8位置的凝固坯殼生長規律；

判斷跟蹤單元位置：根據跟蹤單元生成時記錄的澆鑄總長減去當前時刻的澆鑄總長計算得到跟蹤單元在本周期內到達的位置，并將位置保存到所述跟蹤單元的屬性中，根據所述跟蹤單元所在位置選取邊界條件，同時判斷最后一個跟蹤單元位置，如果最后一個跟蹤單元的位置超過鑄機長度，即認為其移出空冷區，將這個跟蹤單元的所有屬性消除，刪除跟蹤單元，否則繼續下一周期計算。

優選地，所述宏觀偏析檢測采用原位分析或鉆屑取樣分析法。

優選地，建立一維在線熱跟蹤計算模型進行所述溫度場計算，對于每一個所述跟蹤單元進行凝固傳熱計算，其控制方程為：

式中，l為凝固潛熱系數，取值為2.72×10⁵j/kg，ρ為鋼的密度；c為鋼的比熱容；k為鋼的導熱系數；t為鋼的節點溫度；fs為鋼的固相分率。

本發明提供的基于熱物性參數分布計算的有益效果是：將本發明應用于動態壓下系統中去，可以提供給壓下系統更為準確的溫度分布和凝固狀態。這樣動態壓下系統可以依靠準確的凝固狀態來完成動態的壓下過程，而依靠準確的溫度分布可以指定合理的二冷區冷卻制度。本發明計算的坯殼厚度與實測值誤差為5％左右，計算的表面溫度值與實測值溫度的偏差能夠控制住±10℃內。

本發明提供的方法計算更為快速，便捷，主要體現在以下三點：

(1)該方法是微觀與宏觀的單向耦合，即只考慮熱物性參數對宏觀凝固傳熱的影響，因此無需考慮宏、微觀模型的時間統一，可設置時間步長5s，打破了時間步長0.01s的約束；

(2)該方法建立了一維宏觀凝固傳熱計算模型，節點數比二維傳熱縮減兩個數量級；

(3)該方法將熱物性參數存儲在數據庫內，宏觀凝固傳熱計算過程中結合計算位置的元素偏析情況直接調用相應的熱物性參數，省去了海量的微觀模型計算再推導熱物性參數的時間。

本發明的計算方法與常規熱跟蹤計算模型相比，能充分考慮鑄坯不同位置物性參數的差異性，從而更準確的描述鑄坯凝固進程。

附圖說明

圖1為本發明微觀凝固模型示意圖；

圖2q345b鋼凝固相變圖；

圖3為在線熱跟蹤模型流程示意圖；

圖4碳元素對模型的影響：(a)比熱容，(b)導熱系數，(c)密度(d)坯殼生長規律；

圖5為本發明熱跟蹤模型與傳統熱跟蹤模型計算的不同位置的坯殼厚度變化情況；

圖6為原位分析取樣位置；

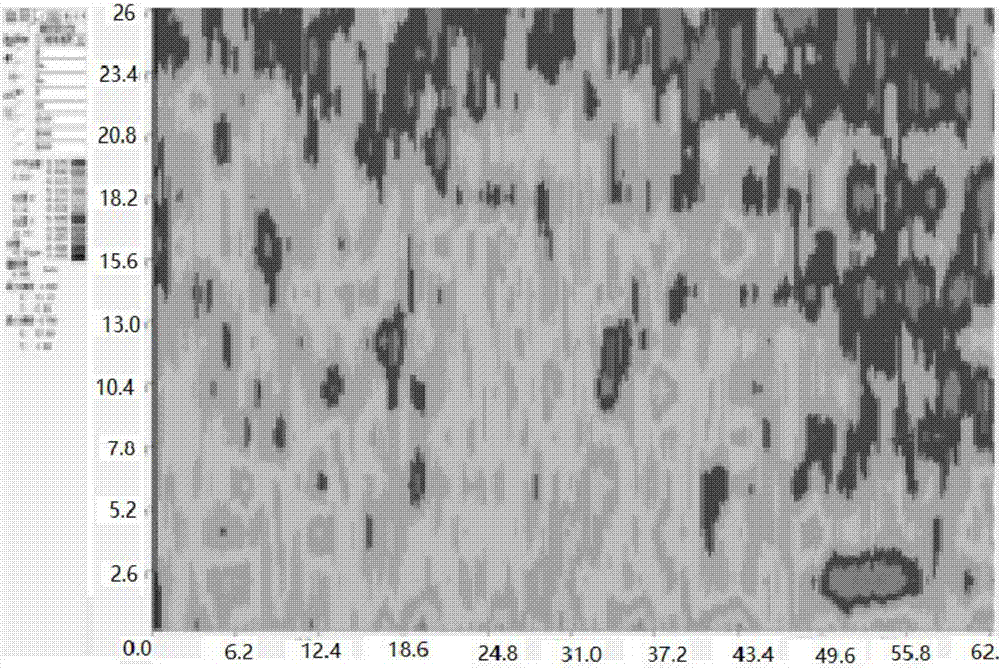
圖7為碳元素含量的二維分布圖；

圖8為磷元素含量的二維分布圖；

圖9為硫元素含量的二維分布圖。

具體實施方式

下面結合附圖，對本發明的具體實施方式作進一步描述。以下實施例僅用于更加清楚地說明本發明的技術方案，而不能以此來限制本發明的保護范圍。

實施例1

本發明提供了一種基于熱物性參數分布計算的連鑄坯熱跟蹤計算方法，包括獲取離線數據和建立鑄坯寬向1/2位置(鑄坯寬向中心位置)在線熱跟蹤計算模型；

獲取離線數據包括以下內容：

(1)離線計算鋼的熱物性參數：采用微觀凝固模型計算不同元素偏析程度條件下鋼的相分率，基于相分率計算鋼的熱物性參數，熱物性參數包括導熱系數、密度和比熱容，并將熱物性參數存儲在數據庫中，具體計算方法如下：

步驟一：以正六邊形枝晶橫截面為基礎建立微觀凝固模型，計算鋼種在凝固過程中的各個相分率，控制方程如下：

式中，為元素i在固相中的溶質濃度，％；t為時間，s；為溶質元素i在固相中的擴散系數，m²/s；

通過微觀凝固模型計算得出鋼種在凝固過程中各個相分率，即分別計算鋼種的液相分率fl、固相分率fs、鐵素體相分率fa、固溶體相分率fδ和奧氏體相分率fγ；

步驟二：利用步驟1得到的鋼種在凝固過程中的各個相分率，計算鋼種的物性參數，包括導熱系數、密度和比熱容，公式如下：

k＝(1-fl)ks+(1+m)flkl(2)

kl＝35(w/km)(3)

式中：k為鋼的導熱系數，w/km；ks和kl分別為鋼種的固相導熱系數和液相導熱系數，fl為鋼種的液相分率，m為經驗常數，取值為4；tl為鋼種的液相線溫度，t為鋼種的節點溫度，wc、wsi、wmn分別為鋼種中的碳含量、硅含量和錳含量，％；

c＝cafa+cδfδ+cγfγ+clfl(5)

cδ＝441.3942+0.17744236t(7)

cγ＝429.8495+0.01497t(8)

cl＝842.6157(9)

式中：c為鋼種的比熱容，j/(kg·℃)；cl、ca、cδ和cγ分別為鋼種的液相、鐵素體、固溶體和奧氏體的比熱，j/(kg·℃)；fl、fa、fδ和fγ分別為鋼種的液相、鐵素體、固溶體和奧氏體相分率；

ρ＝ρlfl+ρδfδ+ργfγ(10)

ρl＝7100-73wc-(0.8-0.09wc)(t-1550)(13)

式中：ρ為鋼種的密度，kg/m³；wc為鋼種中的碳含量，％；ρl、ρδ和ργ分別為鋼種的液相、固溶體相和奧氏體相的密度，kg/m³；

(2)離線獲取鑄坯寬向1/2位置處的凝固坯殼生長規律：利用宏觀偏析檢測獲取鑄坯寬向1/2位置處沿厚度方向上的鑄坯偏析分布規律，形成鋼中元素在鑄坯寬向1/2位置處“鑄坯厚度位置-元素偏析程度”的凝固坯殼生長規律并存儲在數據庫中，本實施例中，宏觀偏析檢測采用原位分析法；

具體為，采用原位分析法測定鑄坯寬向1/2厚度上的溶質偏析，并將“鑄坯厚度位置-元素偏析程度”關系儲存至數據庫以供調用。圖6為原位分析取樣位置，圖7至圖9分別為碳、磷、硫元素的原位分析檢測結果。

(3)針對板坯連鑄需要離線獲取鑄坯寬向不同位置處凝固坯殼生長規律關系：根據二維宏觀凝固傳熱與微觀溶質偏析全耦合計算模型獲取鑄坯寬向1/8位置、1/4位置與寬向1/2位置鑄坯凝固坯殼生長規律關系并存儲在數據庫中，圖e給出了q345b鋼，拉速為0.83m/min拉速條件下不同位置的凝固進程。

使用matlab軟件回歸擬合寬面1/8位置和寬面中心的凝固變化關系式如下：

a1＝1.324e+19

b1＝34.58

c1＝1.843

a2＝2.405e+04

b2＝69.19

c2＝16.51

式中：δ1/8、δcenter分別代表1/8位置和鑄坯中心位置的坯殼厚度，mm；x代表距彎月面的值，a1、a2、b1、b2、c1和c2是擬合得到的系數值，將關系式存入數據庫以供在線計算調用。

上述離線獲取的數據儲存在數據庫中，待在線計算需要時直接調取。

如圖3所示，建立鑄坯寬向1/2位置在線熱跟蹤計算模型包括以下步驟：

步驟1：獲取并讀入鑄坯初始澆鑄條件與澆鑄過程信息：包括鑄坯尺寸、鋼成分、拉速、過熱度、結晶器長度及冷卻量、結晶器進出口水溫差、二冷區劃分及各區實時水量；

步驟2：生成跟蹤單元：在一個周期內，在結晶器彎月面位置生成一個新跟蹤單元，該跟蹤單元的凝固傳熱計算區間為鑄坯寬向1/2位置上沿厚度方向的凝固傳熱，并對跟蹤單元進行溫度和位置的初始化，初始化流程如下：

建立在線熱跟蹤模型的初始條件和邊界條件：

(3-1)初始條件

t0＝ttundish(14)

式中：t0為節點初始溫度，℃；ttundish為澆注溫度，℃；

(3-2)邊界條件

鑄坯中心的邊界條件，依據板坯傳熱的對稱性，斷面溫度的分布以中心對稱分布，即：

鑄坯表面的邊界條件：

式中：qn、qw分別是通過鑄坯表面窄面和寬面的熱通量，w/m²；x和y分別為橫截面窄邊和寬邊的總長，m，k為導熱系數，w/km；

(a)結晶器的邊界條件

鑄坯在結晶器內的傳熱邊界條件設定為：

式中：q為結晶器的熱流密度，mw/m²，a和b為結晶器的待定系數；z為鑄坯距離彎月面的距離，m；

(b)二冷區的邊界條件

將鑄坯與支撐輥接觸導熱傳遞出的熱量，使用增大對流系數的方法來處理，二冷區的等效熱流密度公式如下所示：

q＝hw(ts-tw)+σε[(ts+273.15)⁴-(tw+273.15)⁴](20)

hw＝[1570w^0.55(1-0.0075tw)]/cm(21)

式中：hw為綜合對流換熱系數，w/(m·℃)；t為鑄坯的表面溫度，℃，ts為固相線溫度，℃；tw為冷卻水或環境溫度，℃；σ為玻爾茲曼常數5.67×10^-8w/(m²·k⁴)；ε為鑄坯表面的黑度，通常取0.8，w為水流密度，l/(m²·s)，cm為經驗系數，取值為4.4；

(c)空冷區的邊界條件

連鑄進入空冷區內的主要是通過鑄坯表面輻射傳熱的方式散熱，熱流密度公式如下：

q＝σε[(ts+273.15)⁴-(tw+273.15)⁴](22)

式中，σ為玻爾茲曼常數5.67×10^-8w/(m²·k⁴)，ε為鑄坯表面的黑度，通常取0.8，tw為冷卻水或環境溫度；

步驟3：選取熱物性參數：在一個跟蹤單元內，調用鑄坯初始澆鑄條件與澆鑄過程信息確定鑄坯厚度位置，在數據庫中選擇該厚度位置對應的元素偏析程度，并根據元素偏析程度調用數據庫中該位置對應的熱物性參數；

步驟4：跟蹤單元求解計算：在一個周期內，調用上述熱物性參數，從結晶器液面開始對鑄坯寬向1/2位置的整個連鑄流長中的所有跟蹤單元完成一次溫度場計算，具體計算方法如下；

建立一維在線熱跟蹤計算模型進行溫度場計算，對于每一個跟蹤單元進行凝固傳熱計算，其控制方程為：

式中，l為凝固潛熱系數，取值為2.72×10⁵j/kg，ρ為鋼的密度，kg/m³；c為鋼的比熱容，j/(kg·℃)；k為鋼的導熱系數，w/km；t為鋼的節點溫度，℃；fs為鋼的固相分率；

步驟5：通過已獲取的所述鑄坯寬向1/2位置處的凝固坯殼生長規律和上述鑄坯寬向1/8位置、1/4位置與寬向1/2位置鑄坯凝固坯殼生長規律關系，獲取鑄坯寬向1/4與1/8位置的凝固坯殼生長規律；

步驟6：判斷跟蹤單元位置：根據跟蹤單元生成時記錄的澆鑄總長減去當前時刻的澆鑄總長計算得到跟蹤單元在本周期內到達的位置，并將位置保存到所述跟蹤單元的屬性中，根據上述跟蹤單元所在位置選取邊界條件，同時判斷最后一個跟蹤單元位置，如果最后一個跟蹤單元的位置超過鑄機長度，即認為其移出空冷區，將這個跟蹤單元的所有屬性消除，刪除跟蹤單元，否則繼續下一周期計算。

下面結合附圖1至圖5對基于熱物性參數的在線熱跟蹤模型的流程進行具體的說明：

通過圖1和圖2中的微觀模型完成物性參數的計算，圖1中微觀模型的界面移動主要是使用當前溫度和界面處計算得到tl和溫度進行對比而決定，tl和分別代表鋼的液相線溫度和凝固過程中δ/γ相轉變開始溫度，每經過一個時間步長δt就需要進行一次界面移動的判斷過程。在δ/l和γ/l界面，當液相計算的tl溫度低于當前溫度，將從液相中析出δ或者γ相。同時在δ/γ界面，當δ相節點計算的溫度高于當前溫度，將從δ相中析出γ相。模型假設在凝固過程中首先析出的δ相，這種假設雖不符合實際但只有很小的誤差，當c含量較高時，高于實際溫度，當第一個δ相產生后，會立刻在下一個時間步長δt轉變為γ相。微觀凝固模型在每一個時間步長不僅要完成對界面的移動，還需要根據非金屬夾雜物生產的平衡反應方程式來判斷和計算非金屬夾雜物的析出。熱物性參數計算模塊主要是計算相組成，再通過相組成、溫度及溶質濃度來完成對導熱系數、比熱容和密度計算并存儲，為當前溫度下此鋼成分對應的固相率、導熱系數等物性參數值。

從圖3中可以看出，計算得到的物性參數保存到了數據庫中。在每個周期內，生成一個新的跟蹤單元，并對新的跟蹤單元進行溫度和位置等屬性的初始化。在一個周期內，從結晶器液面開始對整個連鑄流長中的所有跟蹤單元完成一次溫度場計算。邊界條件是根據單元所處的位置來選取相應位置的冷卻參數來計算，物性參數是從數據庫中根據溫度來讀取相應的物性參數。并將單元的溫度分布和凝固狀況保存到跟蹤單元的屬性數組中。計算每個單元在此周期內到達的位置，并將位置保存到跟蹤單元的屬性中，同時對最后一個單元進行判斷，如果最后一個單元的位置移出空冷區，則將這個跟蹤單元的所有屬性消除，刪除跟蹤單元。在生產過程中在線熱跟蹤模型計算得到的結果傳遞給動態壓下控制模型和動態二冷控制模型，這兩個模型再根據溫度分布和凝固狀態的數據進行計算完成對壓下和二冷區的控制操作。

圖4以碳元素為例，比較了不同碳含量條件下熱物性參數的差異性及相應的凝固坯殼生長規律的差異性。如圖4(a)-(c)可以看出，當碳含量發生變化時，鑄坯的比熱容、導熱系數、密度均不相同，因此如圖4(d)所示鑄坯坯殼生長規律也不相同。考慮到連鑄過程中的具體情況從內弧表面到鑄坯中心分為6個不同區域，根據六個區域的元素偏析平均值確定其對應的熱物性參數，并帶入在線熱跟蹤模型的計算中去。

圖5為本發明熱跟蹤模型與傳統熱跟蹤模型計算的不同位置的坯殼厚度變化情況，在圖中，20.5m位置處本發明模型計算的坯殼厚度為116mm，使用傳統熱跟蹤模型在此位置計算的坯殼厚度為129mm，射釘實驗結果為119mm，本發明模型的誤差為2.5％，而傳統模型的誤差為4.4％，因此可以看出本模型計算準確性更好。

以上所述實施例僅為本發明較佳的具體實施方式，本發明的保護范圍不限于此，任何熟悉本領域的技術人員在本發明披露的技術范圍內，可顯而易見地得到的技術方案的簡單變化或等效替換，均屬于本發明的保護范圍。