一種直線進給系統的導軌直線度測量裝置及方法與流程
本發明涉及機床加工精度的測量,具體為一種直線進給系統的導軌直線度測量裝置及方法。
背景技術:
機床加工精度是評定機床綜合性能的關鍵標準,當今國外的先進精密機床的加工精度已經達到1μm~0.1μm,超精密級別機床的加工精度已經高于0.1μm,這標志著機床行業的加工精度已經進入納米級時代。而我國在此精度級別的精密機床無論在精度、一致性保證等方面都與國際領先水平存在著明顯差距。研究表明機床加工誤差來源主要包括準靜態誤差,例如幾何誤差、熱誤差;加工過程中誤差,例如刀具誤差、夾具誤差等;檢測誤差,例如不確定性誤差、安裝誤差等。
在精密機床裝配過程中,測量方法和工具合理選取對整個裝配起著至關重要的作用,高效精準的測量方法能夠有效提升整個裝配工藝的效率和精度。現行幾種導軌直線度的測量方法不能滿足高精密機床裝配工藝的測量精度要求,因此一種高效準確的導軌幾何誤差的測量方法對于直線進給系統精度保障和預測模型的實際應用,特別是高精密機床的裝配工藝優化都顯得尤為重要。同時,實際生產中,直線進給系統中導軌的水平和豎直方向的直線度誤差是精度設計和裝配環節中主要的精度指標,這些誤差都是在設計和裝配過程中可以直接控制的精度項,而直線進給系統的目標精度即工作臺的運動誤差是無法直接調控的,這也為直線進給系統中精度保證帶來了障礙。
技術實現要素:
針對現有技術中存在的問題,本發明提供一種直線進給系統的導軌直線度測量裝置及方法,提升了導軌直線度的測量精度和測量的簡易性。
本發明是通過以下技術方案來實現:
一種直線進給系統的導軌直線度測量裝置中直線進給系統的導軌基準坐標系為以豎直方向為Z軸,滑塊的移動方向為Y軸,水平垂直遠離導軌的方向為X軸;
其包括分別固定在滑塊上的第一測量夾具和第二測量夾具;固定在第一測量夾具上的激光準直儀,分別對稱設置在第二測量夾具X向上的二號位移傳感器和三號位移傳感器,以及設置在第二測量夾具Z向上的一號位移傳感器;激光準直儀的光路與第一測量夾具Y向平行;一號位移傳感器的中心線經過激光準直儀的中心點;二、三、一號位移傳感器位于同一個垂直于Y向的平面內;二號位移傳感器和三號位移傳感器分別用于測量導軌與滑塊之間Y向的位移間隙;一號位移傳感器和激光準直儀用于測量滑塊和導軌之間Z向位移間隙。
優選的,第一測量夾具固定于兩個成間隙設置的滑塊上;第二測量夾具設置在兩個滑塊的間隙中,且固定在第一測量夾具上。
優選的,二、三和一號位移傳感器均采用電渦流位移傳感器,測量精度為0.25um。
優選的,激光準直儀的測量距離為0-15m,測量精度為0.1um。
一種直線進給系統的導軌直線度測量方法,包括如下步驟,
步驟1,建立如權利要求1所述的測量裝置,確定第一測量夾具和第二測量夾具以及三個位移傳感器和激光準直儀之間的幾何關系,建立對應的幾何模型;
步驟2,根據建立的幾何模型,以激光準直儀的激光光路作為基準,通過激光準直儀測量得到導軌的直線度分別如下,
豎直方向的測量值為ez(yi)=Bz+mz(yi)-h1-d1(yi);
水平方向的測量值為
其中,Bz是激光基準與導軌豎直方向上的距離,mz(yi)為準直儀豎直方向讀數,h1為一號位移傳感器接收面與激光準直儀中心豎直方向上的距離,d1(yi)為一號位移傳感器的讀數;
Bx是激光基準與導軌水平方向的距離,Gx是導軌左右兩側面的測量值之差,l2為二號位移傳感器與激光準直儀水平方向上的距離,l3為三號位移傳感器與激光準直儀水平方向上的間距,mx(yi)為激光準直儀豎直方向讀數,d2(yi)為二號位移傳感器的讀數,d3(yi)為三號位移傳感器的讀數。
優選的,步驟2中,
Gx=e2x(yi)-e1x(yi),
且e2x(yi)=Bx+mx(yi)+l2-d2(yi),e1x(yi)=Bx+mx(yi)-l3+d3(yi),
其中,e2x(yi)和e1x(yi)分別為對于導軌左右側面的測量值,mx(yi)為激光準直儀豎直方向讀數,d2(yi)和d3(yi)為二號、三號位移傳感器的讀數。
優選的,步驟1中,還包括如下步驟,
步驟1.1,根據建立的幾何模型,建立直線位移誤差與三個位移傳感器測得量和裝置設計尺寸之間的數學關系模型;
步驟1.2,根據建立的數學模型,分析豎直方向和水平方向的測量誤差來源分析;
步驟1.3,根據誤差來源分析公式,設計激光準直儀和三個傳感器與導軌和兩個夾具之間的相對尺寸大小。
進一步,由步驟1.3得到,位移傳感器測量平面與激光準直儀接收器的接受平面,在行程向距離的裝配誤差小于等于4mm。
進一步,由步驟1.3得到,h1和h2至少大于25mm。
與現有技術相比,本發明具有以下有益的技術效果:
本發明所述裝置主要由激光準直儀、測量裝置夾具和三個位移傳感器三部分組成,激光準直儀和三個位移傳感器通過測量裝置夾具固定在兩個導軌滑塊上,測量裝置在導軌上往復運動,其中激光準直儀用于測量滑塊所在位置的上表面和側面距離測得裝置的距離,從而能夠簡單準確的得到導軌直線度,結構簡單,使用方便。
本發明所述方法利用激光作為測量基準,提高測量基準的準確性;通過激光準直儀測量滑塊運動直線度誤差作為間接基準;該方法提升了導軌直線度的測量精度和測量的簡易性。通過位移傳感器比較導軌直線度誤差和滑塊運動直線度誤差之間的差值,通過測量量補償以滑塊運動直線度誤差代替導軌直線度誤差引起的測量誤差,從而對其裝置的幾何關系進行準確限定,保證了測量精度。
進一步的,通過分析導軌的幾何誤差和工作臺的運動誤差之間的傳遞關系,以此為基礎構建直線進給系統運動精度預測模型,通過實驗來得到直線進給系統兩個直線度的誤差,對理論化的直線進給系統精度設計與裝配工藝規劃進行指導限定,通過測量裝置的設計來盡可能的減小角度誤差對直線度誤差的影響。
附圖說明
圖1為本發明實例中豎直方向幾何誤差與準直儀和傳感器讀數之間的關系示意圖。
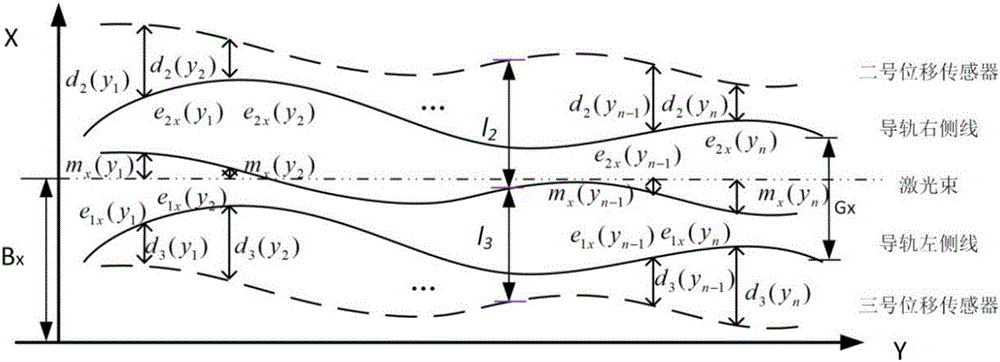
圖2為本發明實例中水平方向幾何誤差與準直儀和傳感器讀數之間的關系示意圖。
圖3a為本發明實例中測量裝置的結構正視圖。
圖3b為本發明實例中測量裝置在位移傳感器處的剖視圖。
圖4a為本發明實例中測量裝置安裝位置正視圖。
圖4b為本發明實例中測量裝置安裝位置在位移傳感器處的剖視圖。
圖5為本發明實例中實驗測量方法及驗證流程圖。
圖6為本發明實例中直線度誤差來源分析豎直方向測量時測量裝置各個坐標系的位置關系。
圖中:第一測量夾具1,第二測量夾具2,二號位移傳感器3,三號位移傳感器4,一號位移傳感器5,激光準直儀6。
具體實施方式
下面結合具體的實施例對本發明做進一步的詳細說明,所述是對本發明的解釋而不是限定。
本發明所述的測量裝置,如圖3a和圖3b所示,其包括連接激光準直儀6和導軌滑塊的第一測量夾具1,固定二號位移傳感器3和三號位移傳感器4的第二測量夾具2,測量導軌與滑塊之間Y向位移間隙的二號位移傳感器3和三號位移傳感器4,用于測量滑塊和導軌之間Z向位移間隙的一號位移傳感5以及激光準直儀6。其基準坐標系為以豎直方向為Z軸,滑塊的移動方向為Y軸,水平垂直遠離導軌的方向為X軸。
如圖4a和圖4b所示,在測量裝置的安裝過程中,LY,LX,LZ分別表示激光準直儀接收器的長寬高,是由激光準直儀型號決定的,l1是傳感器測量平面與激光準直儀接收器的接受平面在行程向的距離,為了減少旋轉引起的誤差,裝置在水平誤差測量時采用對稱設計的;l2表示二號位移傳感器測量頭與激光準直儀接收器中心水平方向的距離,因為采用對稱設計,三號位移傳感器測量頭與激光準直儀接收器中心水平方向的距離同為l2;h1和h2分別表示一、二號位移傳感器測量頭與激光準直儀接收器中心在豎直方向的距離。為了確定這些關鍵尺寸的大小需要分別分析在測量導軌豎直和水平方向幾何誤差過程中的誤差來源和誤差傳遞關系。
本發明所述的方法,如圖5所示,首先建立相應的幾何模型,設計相關的實驗裝置,為了檢測導軌的直線度誤差,接下來需要建立相關的數學模型,推導出在X方向和Y方向上誤差與其他參數的數學關系,得出影響導軌直線度誤差的因素,下一步就是為了消除其他因素對直線度誤差的影響,對導軌直線度誤差測量裝置關鍵尺寸進行設計,從而消除一些附加因素帶來的誤差。接下來對水平方向直線度和豎直方向直線度誤差來源進行分析,最后利用三坐標測量儀進行驗證。
具體的,本發明包括如下步驟。
1、基于激光準直儀的組合式導軌直線度測量原理幾何模型設計:
為了實現導軌直線度的測量,需要合理設計裝置的一些尺寸參數,需要設計的尺寸包括,二號位移傳感器3與激光準直儀6基準在豎直方向的距離h1,激光基準與導軌面豎直方向的距離BZ,二號位移傳感器的測量頭與激光準直儀6接收器中心水平方向的距離l2,二號位移傳感器的測量頭與激光準直儀接收器中心在豎直方向上的距離h2。在這里選擇激光準直儀的型號GEPARD5-M4,尺寸大小為140mm×50mm×50mm,其測量距離為0-15m,測量精度為0.1um,選擇位移傳感器的型號CS05,測量精度為0.25um。
2、基于激光準直儀的組合式導軌直線度測量原理數學模型設計:
通過對實驗裝置的設計,可以通過幾何關系得出以下結論:利用激光準直儀測得的水平方向上的讀數為mx(y),豎直方向上的讀數為mz(y),二、三、一號位移傳感器3、4、5布放在同一個垂直于Y軸的平面內,設三個傳感器分別測得的距離讀數為d1(y)、d2(y)、d3(y),在忽略裝置運動過程中的旋轉誤差的理想情況下,以豎直方向為例,ez(yi)、mz(yi)、d1(yi)之間的關系如式1所示,其幾何關系如圖1所示。
ez(yi)=Bz+mz(yi)-h1-d1(yi) (1)
h1為一號位移傳感器與激光準直儀豎直方向上的距離,Bz是激光基準與導軌豎直方向上的距離,都為固定值,所以測量裝置在yi位置時,導軌豎直方向的測量值ez(yi)、mz(yi)為準直儀豎直方向讀數,d1(yi)為一號位移傳感器的讀數。利用激光準直儀6測得的水平方向上的讀數為mx(y),豎直方向上的讀數為mz(y),二、三、一號位移傳感器3、4、5布放在同一個垂直于Y軸的平面內,設三個傳感器分別測得的距離讀數為d1(y)、d2(y)、d3(y),在忽略裝置運動過程中的旋轉誤差的理想情況下,以水平方向為例,ex(yi)、mx(y)、d1(y)之間的關系如式2所示幾何關系如圖2所示:
對于左右側面導軌的測量值e2x(yi),e1x(yi),準直儀豎直方向讀數為mx(yi)和二號、三號位移傳感器的讀數d2(yi)、d3(yi)之間的關系為:
e2x(yi)=Bx+mx(yi)+l2-d2(yi) (2)
e1x(yi)=Bx+mx(yi)-l3+d3(yi) (3)
對于直線進給系統裝配中使用的成品的精密直線導軌而言,同一根導軌的其左右側面導軌的幾何誤差具有良好的一致性,所以可以認為:Gx=e2x(yi)-e1x(yi)所以有:
其中:l2為二號位移傳感器與激光準直儀水平方向上的距離,l3為三號位移傳感器與激光準直儀水平方向上的間距,Bx是激光準直與導軌水平方向的距離,ex(yi)為導軌水平方向的測量值、mx(yi)為準直儀豎直方向讀數,d2(yi)為二號位移傳感器的讀數,d3(yi)為三號位移傳感器的讀數。
具體的通過如下步驟對本發明的誤差進行分析優化。
1、基于激光準直儀的組合式導軌直線度測量豎直方向和水平方向測量誤差來源分析:
為了準確的計算測量值需要設計放置激光準直儀移動端和三個位移傳感器的安裝裝置。需要利用測量的誤差來源分析分別確定三個位移傳感器的安裝尺寸設計和激光準直儀的安裝尺寸。
實驗測量裝置在導軌滑塊的移動端和固定端的測量元件位置布置以及安裝尺寸的確定;假設了裝置在運動過程中只存在水平和豎直方向的偏移,且忽略了裝配過程中的裝配引起的誤差,但是在實際情況中,整個裝置在導軌上運動時,除了水平和豎直方向上的運動誤差,還存在繞X軸旋轉誤差即俯仰誤差α,繞Y軸旋轉即滾轉誤差β,繞Z軸旋轉誤差即偏擺誤差γ,激光準直儀實測的值和位移傳感器的測量量都會受到旋轉誤差作用引起測量誤差,所以在裝置的設計過程中,需要對于關鍵尺寸和機構進行設計,以減小旋轉誤差。整個裝置中的關鍵尺寸主要指激光準直儀的位置和三個傳感器的布放。
關鍵尺寸主要有:Ly、Lx和Lz分別表示激光準直儀接收器的長寬高,是由激光準直儀型號決定的;l1是傳感器測量平面與激光準直儀接收器的接受平面在行程向的距離,為了減少旋轉引起的誤差,裝置在水平誤差測量時采用對稱設計的;l2表示二號位移傳感器測量頭與激光準直儀接收器中心水平方向的距離,因為采用對稱設計,三號位移傳感器測量頭與激光準直儀接收器中心水平方向的距離l3同為l2;h1和h2分別表示一號和二號位移傳感器測量頭與激光準直儀接收器中心在豎直方向的距離。為了確定這些關鍵尺寸的大小需要分別分析在測量導軌豎直和水平方向幾何誤差過程中的誤差來源和誤差傳遞關系。
如圖1所示,豎直方向幾何誤差與準直儀和傳感器讀數之間的關系中,其中h1為一號位移傳感器接收面與激光準直儀中心豎直方向的距離,Bz是激光準直與導軌豎直方向的距離,都為固定值,所以測量裝置在yi位置時,導軌豎直方向的測量值ez(yi)、mz(yi)為準直儀豎直方向讀數,d1(yi)為一號位移傳感器的讀數。
如圖2所示,水平方向幾何誤差與準直儀和傳感器讀數之間的關系中,其中l2為二號位移傳感器與激光準直儀水平方向上的距離,l3為三號位移傳感器與激光準直儀水平方向上的間距,Bx是激光準直與導軌水平方向的距離,ex(yi)為導軌水平方向的測量值、mx(yi)為準直儀豎直方向讀數,d2(yi)為二號位移傳感器的讀數d3(yi)為三號位移傳感器的讀數。
如圖6所示,直線度誤差來源分析豎直方向測量時測量裝置各個坐標系的位置關系。首先在整個測量系統中建立坐標系,設激光光路的坐標系為坐標系P1,光路為Y軸;在準直儀的接收平面建立坐標系P2,XOZ平面與接收面重合,原點與接收面中心重合;坐標系P3為一號位移傳感器的接收面的坐標系,原點與接收面圓心重合,ZOY平面與接收平面重合;坐標系P4為導軌的頂平面,ZOY平面與頂平面重合。
具體的,分析在測量導軌豎直和水平方向幾何誤差過程中的誤差來源和誤差傳遞關系,首先給定一些參數的初值,利用不同坐標系之間的位置關系,通過齊次坐標變換的方法,從激光光路的坐標系P1傳遞到導軌測量面的坐標系P4,變換公式如下:
豎直方向的測量誤差就是求解坐標系P4相對于坐標系P1在豎直方向的偏移量與理論偏移量z′4=d1+mz+Δz23之間的差值,則利用齊次坐標變換的原理,由于實際測量過程中各坐標系間偏轉角度誤差很小,
所以有:
其中,Δxmn、Δymn、Δzmn分別表示坐標系Pm的原點在Pn中的位置,αmn、βmn、γmn分別表示坐標系Pm相對于Pn的X、Y、Z軸的旋轉角度,最后求得:
得出:
z4=-α23α34mz+α34γ23mx-β23β34mz+α34Δy23-β23mx-β34mx-β34Δx23+d1+mz+Δz23 (6)
因為理論偏移量
z′4=d1+mz+Δz23 (7)
所以豎直方向的主要誤差大小為:
ξz≈α34l1-β23mx-β34mx (8)
同理可得在水平方向
x′4=(-β2′3β3′4-γ2′3γ3′4)mx+(α2′3γ3′4+β2′3+β34)mz+β3′4h2-γ3′4l1+l2-d2+mx(9)
因為理論偏移量為
x4=d1+mz+Δz23 (10)
所以水平方向的主要誤差大小為:
ξx≈(β2′3+β3′4)mz+β3′4h2-γ3′4l1 (11)
2、基于激光準直儀的組合式導軌直線度誤差測量裝置的關鍵尺寸設計:
通過分析豎直方向和水平方向的誤差來源,可以看到在豎直方向誤差來源主要有α34、β23、β34、mx、l1五項組成,其中主要的設計尺寸為l1,l1為一號位移傳感器的中心與激光準直儀的接受面在行程向上距離,設計階段本文在結構設計中使其為零,以最大程度減小l1對測量精度的影響,在裝置的裝配過程中,同樣要l1的裝配誤差盡可能的小,由于α34≤2×10-4rad所以要求l1的裝配誤差小于等于4mm,這種情況下由α34l1引起的誤差大小小于1μm。
在水平方向誤差來源主要有β'23、β'34、γ'34、mz、h2、l1,六項組成,其中β'23、β'34、γ'34為不可消除誤差,h2主要由激光準直儀的結構尺寸決定,必須要至少大于25mm,使用一個位移傳感器時,這部分誤差由于力臂h2過長,放大了測量裝置的扭轉誤差而產生了誤差。
同時可以看出如果在導軌的對稱位置再放置一個位移傳感器,由于二者的力臂長度都為h2,且旋轉角度相同,β3′4=β3″4,所以兩者這部分誤差的增量的大小相同,且方向相反,由此可以看出使用雙位移傳感器測量取均值可以有效的消除h2在水平方向測量中產生的誤差l2=l3。
同理分析γ3′4l1可知雙位移傳感器的測量方法也可以抵消這部分誤差。所以本文設計采用雙位移傳感器測量導軌的幾何誤差。
水平方向的測量誤差由于對稱結構的均化效果,消除了結構尺寸參數對其的影響,只受到裝置裝配誤差的影響,通過嚴格的裝配工藝要求可以進一步大幅提升了測量的精度。
具體的通過如下步驟對本發明得到的直線度進行驗證。
直線導軌直線度誤差測量方法不確定度分析:
對基于激光準直儀和位移傳感器組成的導軌直線度測量方法進行不確定度分析,表1表示激光準直儀每個測量位置的測量標準差。
表1激光準直儀每個測量位置的測量標準差單位μm
表2位移傳感器每個測量位置的測量標準差單位μm
根據表1和表2可以確定該測量裝置對于水平和豎直方向的測量單點不確定度。綜上,依據標準不確定的A類的評定方法中的貝塞爾法,可以確定此次測量中兩根導軌的水平和豎直方向的測量不確定度如表3所示:
表3測量裝置此次測量的不確定度單位μm
綜上所述:采用本發明的一種由激光準直儀和位移傳感器組成的導軌直線度測量方法,可以有效的測量直線進給過程中導軌的直線度誤差,從而為直線進給系統運動精度預測模型在直線進給系統的實際生產中的應用奠定了基礎。
- 還沒有人留言評論。精彩留言會獲得點贊!