一種多星約束穩健空頻抗干擾處理方法和裝置與流程

本發明涉及通信領域，尤指一種多星約束穩健空頻抗干擾處理方法和裝置。

背景技術：

為了在復雜電磁環境中抑制掉強壓制式干擾，陣列天線波束形成技術廣泛應用于擴頻通信系統。然而自適應波束形成技術對于期望信號導向矢量的失配非常敏感，由于存在這種失配會使陣列波束形成器把期望信號進行一定程度抑制，因此被稱為信號的自相消。

傳統的波束形成算法不能改善未知傳感器互耦、近場波前失真、源擴展以及相干和非相干的局部散射等影響，因此穩健的波束形成技術越來越成為波束形成研究中的重點和熱點。

技術實現要素：

為了解決上述技術問題，本發明提供了一種多星約束穩健空頻抗干擾處理方法和裝置，可以解決由于期望信號導向矢量的失配等原因引起的輸出信干噪比惡化問題，增強了算法穩健性。

為了達到本發明目的，本發明提供了一種多星約束穩健空頻抗干擾處理方法，包括：

將接收到的時域信號通過傅立葉變換，轉換為頻域數據；

根據所述頻域數據計算信號帶寬內頻點的協方差矩陣，確定協方差矩陣修正因子，根據所述協方差矩陣修正因子計算權向量；

使用所述權向量對所述頻域數據進行濾波處理；

對濾波后的頻域數據進行傅里葉逆變換，轉換為時域數據并輸出。

可選地，所述根據所述頻域數據計算信號帶寬內頻點的協方差矩陣，確定協方差矩陣修正因子，根據所述協方差矩陣修正因子計算權向量的步驟中，

對頻域數據采用分段處理的方式，通過設置所述權向量中部分矢量為零，以將期望信號帶外部分進行清零處理。

可選地，所述確定協方差矩陣修正因子的步驟中，

所述協方差矩陣修正因子α/β通過下式計算得到：

α/β＝γtr(R_k)/M，γ＝1-e^-0.1M

其中，R_k為所述協方差矩陣，M為所述協方差矩陣的維數，tr()表示矩陣的跡。

可選地，所述方法還包括：

利用先驗信息估計衛星波達方向，確定空頻導向矢量。

可選地，所述根據所述協方差矩陣修正因子計算權向量的步驟中，分別對每個頻點的權向量進行計算，所述權向量w(f_k)通過下式計算得到：

其中，f_k表示第k個頻點，為樣本協方差矩陣，α/β為協方差矩陣修正因子，I為單位陣，A為空頻導向矢量，b為N×1維的全1列向量，N為所述時域信號的個數。

本發明還提供一種多星約束穩健空頻抗干擾處理裝置，應用于空頻自適應處理器，包括：

第一信號轉換模塊，用于將接收到的時域信號通過傅立葉變換，轉換為頻域數據；

計算模塊，用于根據所述頻域數據計算信號帶寬內頻點的協方差矩陣，確定協方差矩陣修正因子，根據所述協方差矩陣修正因子計算權向量；

濾波模塊，用于使用所述權向量對所述頻域數據進行濾波處理；

第二信號轉換模塊，用于對濾波后的頻域數據進行傅里葉逆變換，轉換為時域數據并輸出。

可選地，所述計算模塊，進一步用于對頻域數據采用分段處理的方式，通過設置所述權向量中部分矢量為零，以將期望信號帶外部分進行清零處理。

可選地，所述計算模塊，進一步用于通過下式計算得到所述協方差矩陣修正因子α/β：

α/β＝γtr(R_k)/M，γ＝1-e^-0.1M

其中，R_k為所述協方差矩陣，M為所述協方差矩陣的維數，tr()表示矩陣的跡。

可選地，所述計算模塊，還用于利用先驗信息估計衛星波達方向，確定空頻導向矢量。

可選地，所述計算模塊，進一步用于分別對每個頻點的權向量進行計算，通過下式計算得到權向量w(f_k)：

其中，f_k表示第k個頻點，為樣本協方差矩陣，α/β為協方差矩陣修正因子，I為單位陣，A為空頻導向矢量，b為N×1維的全1列向量，N為所述時域信號的個數。

與現有技術相比，本發明實施例通過采用協方差矩陣修正因子計算權向量，可以保證多顆衛星信號數據失配時仍能有效地抑制寬帶干擾，增強了空域濾波算法的穩健性。進一步地，通過對帶外信號進行清零處理，在保證濾波效果的前提下，簡化了工程運算量。

附圖說明

附圖用來提供對本發明技術方案的進一步理解，并且構成說明書的一部分，與本申請的實施例一起用于解釋本發明的技術方案，并不構成對本發明技術方案的限制。

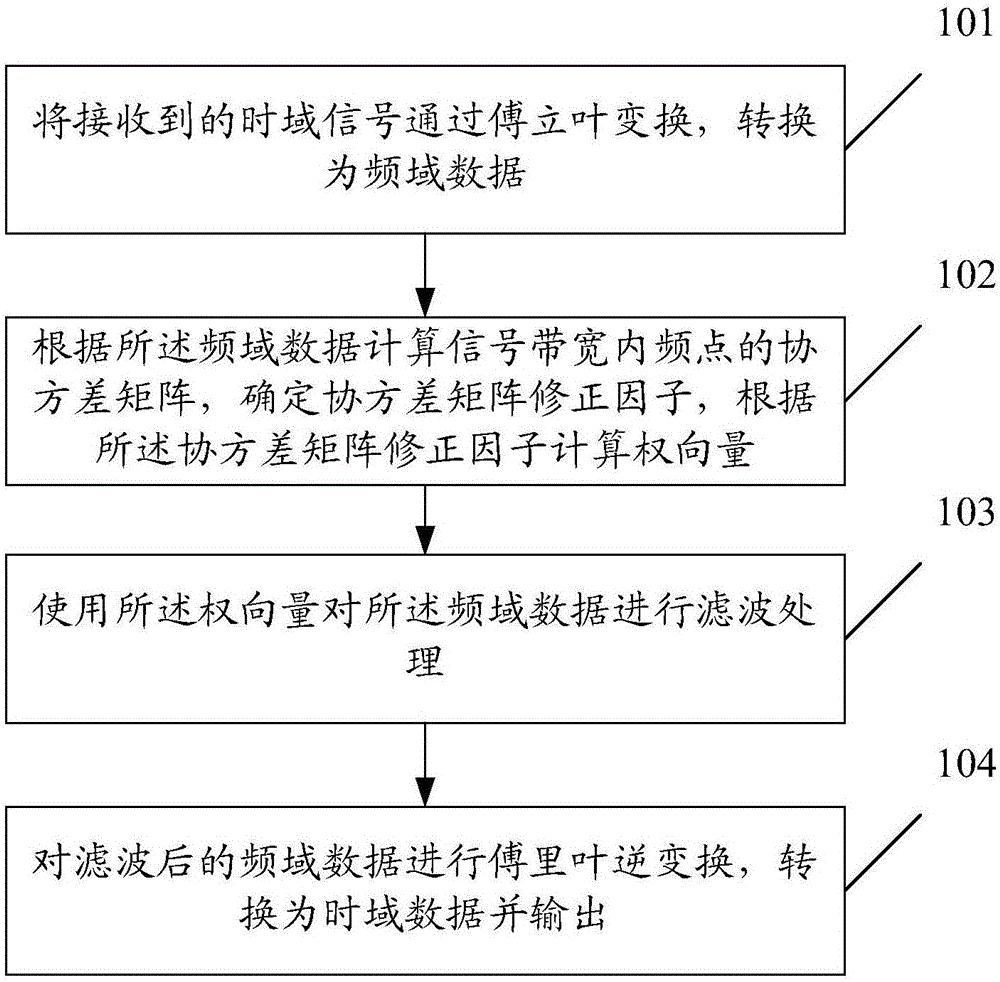
圖1為本發明實施例的多星約束穩健空頻抗干擾處理方法流程圖；

圖2為本發明應用示例的示意圖；

圖3為本發明實施例的多星約束穩健空頻抗干擾處理裝置示意圖；

圖4為本發明應用示例的空頻自適應處理器內部處理過程示意圖。

具體實施方式

為使本發明的目的、技術方案和優點更加清楚明白，下文中將結合附圖對本發明的實施例進行詳細說明。需要說明的是，在不沖突的情況下，本申請中的實施例及實施例中的特征可以相互任意組合。

在附圖的流程圖示出的步驟可以在諸如一組計算機可執行指令的計算機系統中執行。并且，雖然在流程圖中示出了邏輯順序，但是在某些情況下，可以以不同于此處的順序執行所示出或描述的步驟。

如圖1所示，本發明實施例的多星約束穩健空頻抗干擾處理方法包括如下步驟：

步驟101，將接收到的時域信號通過傅立葉變換，轉換為頻域數據；

所述傅立葉變換可以是快速傅立葉變換(FFT)或者離散傅立葉變換(DFT)。

對于寬帶接收機，考慮N個遠場的寬帶信號s_i,i＝1,2,...N(包括期望信號和干擾)以θ_i,i＝1,2,...N方向入射到空間M元均勻線陣上，通常假設第1項s₁對應于感興趣的期望信號，而s_i,i＝2,...N對應于N-1個干擾信號。陣列單元間距為接收信號最高頻率對應的波長的一半。假設信號的帶寬為B，則第m個陣元的接收數據

其中τ_mi表示第m個陣元上接收的第i個信號的延時，n_m(t)為第m個陣元通道的熱噪聲。

在步驟101之前，本發明實施例還可包括：利用先驗信息估計衛星波達方向，確定空頻導向矢量。

其中，利用先驗信息估計當前N顆可見衛星的波達方向θ_i,i＝1,2,...N，求解出對應空頻導向矢量A(f_k)＝[a(θ₁,f_k)a(θ₂,f_k)...a(θ_N,f_k)]，以均勻線陣為例，波達方向為θ₁的衛星信號空頻導向矢量為

其中d為陣元間距，M為陣元數，c為光速常數。

如圖2所示，采用M陣元的空頻二維處理器結構，對各陣元中頻AD(模擬信號轉換為數字信號)采樣信號進行K點傅立葉變換變換得到頻域數組x₁₁,x₁₂,…x_1K；x₂₁,x₂₂,…x_2K；…x_M1,x_M2,…x_MK，數據中包含衛星信號、干擾以及噪聲。

步驟102，根據所述頻域數據計算信號帶寬內頻點的協方差矩陣，確定協方差矩陣修正因子，根據所述協方差矩陣修正因子計算權向量；

采樣數據經過K點的傅立葉變換后，有1＜B₁＜B₂＜K，B₁、B₂、K均為正整數，其中區間[B₁,B₂]為期望信號帶寬。為了對數據進行有效的處理，同時降低計算復雜度，可以對頻域數據采用分段處理的方式，對于期望信號帶外部分進行清零處理，減少不必要的計算工作。

即：對于頻點f_k，k∈[1,B₁)or(B₂,K]的頻域數據，有w(f_k)＝O_M×1，O_M×1為M×1維的零矢量。

對于頻點f_k，k∈[B₁,B₂]的頻域數據，進行后續處理。

根據頻域數組，計算信號帶寬內頻點的協方差矩陣R_k＝E[X(f_k)X^H(f_k)](M×M維)，其中X(f_k)＝[x_1k,x_2k,...,x_Mk]^T k∈[B₁,B₂]；

其中，R_k為期望的協方差矩陣，在實際應用中，R通常由樣本協方差矩陣代替，在空頻二維濾波器中，對應于頻點f_k的采樣數據的頻域協方差矩陣可表示為如下M×M維的矩陣：

其中L表示頻域數據的快拍數，而x_mk(l)表示第m個陣元采樣數據經過傅立葉變換之后對應頻點f_k上的第l個快拍數。

修正協方差矩陣為α、β為大于0的組合參數，使修正協方差矩陣逼近期望的協方差矩陣，根據最小方差準則有，

tr()表示矩陣的跡，求解得

求解協方差矩陣修正因子α/β，由于實時性要求，信號帶內頻域數據協方差積累時間有限，當陣元數M較大，空間自由度多于衛星數，導向矢量估計值偏差大，權值訓練的數據與權值應用的數據之間失配嚴重，α/β取值越大，反之越小。

在本實施例中，α/β＝γtr(R_k)/M，γ＝1-e^-0.1M。

多星約束方程如下：

Min E{|Y(f_k)|²}＝w(f_k)^HR(f_k)w(f_k)

s.t.A^H(f_k)w(f_k)＝b

則求解權向量表達式為，

根據協方差矩陣修正因子計算權向量其中I是單位陣，b為N×1維的全1列向量。

在本步驟中，通過采用協方差矩陣修正因子，對樣本協方差矩陣進行修正，可以保證多顆衛星信號數據失配時仍能有效地抑制寬帶干擾，增強了空域濾波算法的穩健性。

步驟103，使用所述權向量對所述頻域數據進行濾波處理；

利用權值w(f_k)對頻域數組進行濾波處理，設Y(f_k)為第k個頻點空域濾波的輸出，則

在本步驟中，由于對于頻點f_k，k∈[1,B₁)or(B₂,K]的頻域數據，有w(f_k)＝O_M×1，O_M×1為M×1維的零矢量，所以可以將期望信號帶外部分進行清零處理，降低了運算量和運算復雜度。

步驟104，對濾波后的頻域數據進行傅里葉逆變換，轉換為時域數據并輸出。

其中，可以對空域濾波后的頻域數據Y(f_k)進行K點IFFT(或IDFT)變換，得到抗干擾處理后的時域中頻數據。

如圖2所示，所述時域中頻數據發送至導航處理單元進行下一步處理。

如圖3所示，為本發明實施例的多星約束穩健空頻抗干擾處理裝置，應用于空頻自適應處理器，包括：

第一信號轉換模塊21，用于將接收到的時域信號通過傅立葉變換，轉換為頻域數據；

所述傅立葉變換可以是快速傅立葉變換(FFT)或者離散傅立葉變換(DFT)。

計算模塊22，用于根據所述頻域數據計算信號帶寬內頻點的協方差矩陣，確定協方差矩陣修正因子，根據所述協方差矩陣修正因子計算權向量；

可選地，所述計算模塊22，還用于利用先驗信息估計衛星波達方向，確定空頻導向矢量。

其中，利用先驗信息估計當前N顆可見衛星的波達方向θ_i,i＝1,2,...N，求解出對應空頻導向矢量A(f_k)＝[a(θ₁,f_k)a(θ₂,f_k)...a(θ_N,f_k)]，以均勻線陣為例，波達方向為θ₁的衛星信號空頻導向矢量為

其中d為陣元間距，M為陣元數，c為光速常數。

可采用M陣元的空頻二維處理器結構，對各陣元中頻AD采樣信號進行K點傅立葉變換變換得到頻域數組x₁₁,x₁₂,…x_1K；x₂₁,x₂₂,…x_2K；…x_M1,x_M2,…x_MK，數據中包含衛星信號、干擾以及噪聲。

采樣數據經過K點的傅立葉變換后，有1＜B₁＜B₂＜K，B₁、B₂、K均為正整數，其中區間[B₁,B₂]為期望信號帶寬。為了對數據進行有效的處理，同時降低計算復雜度，可以對頻域數據采用分段處理的方式，對于期望信號帶外部分進行清零處理，減少不必要的計算工作。

即：對于頻點f_k，k∈[1,B₁)or(B₂,K]的頻域數據，有w(f_k)＝O_M×1，O_M×1為M×1維的零矢量。

對于頻點f_k，k∈[B₁,B₂]的頻域數據，進行后續處理。

根據頻域數組，計算信號帶寬內頻點的協方差矩陣R_k＝E[X(f_k)X^H(f_k)](M×M維)，其中X(f_k)＝[x_1k,x_2k,...,x_Mk]^T k∈[B₁,B₂]；

其中，R_k為期望的協方差矩陣，在實際應用中，R通常由樣本協方差矩陣代替，在空頻二維濾波器中，對應于頻點f_k的采樣數據的頻域協方差矩陣可表示為如下M×M維的矩陣：

其中L表示頻域數據的快拍數，而x_mk(l)表示第m個陣元采樣數據經過FFT之后對應頻點f_k上的第l個快拍數。

修正協方差矩陣為α、β為大于0的組合參數，使修正協方差矩陣逼近期望的協方差矩陣，根據最小方差準則有，

tr()表示矩陣的跡，求解得

求解協方差矩陣修正因子α/β，由于實時性要求，信號帶內頻域數據協方差積累時間有限，當陣元數M較大，空間自由度多于衛星數，導向矢量估計值偏差大，權值訓練的數據與權值應用的數據之間失配嚴重，α/β取值越大，反之越小。

在本實施例中，α/β＝γtr(R_k)/M，γ＝1-e^-0.1M。

多星約束方程如下：

Min E{|Y(f_k)|²}＝w(f_k)^HR(f_k)w(f_k)

s.t.A^H(f_k)w(f_k)＝b

則求解權向量表達式為，

根據協方差矩陣修正因子計算權向量其中I是單位陣，b為N×1維的全1列向量。

所述計算模塊22，通過采用協方差矩陣修正因子，對樣本協方差矩陣進行修正，可以保證多顆衛星信號數據失配時仍能有效地抑制寬帶干擾，增強了空域濾波算法的穩健性。

濾波模塊23，用于使用所述權向量對所述頻域數據進行濾波處理；

利用權值w(f_k)對頻域數組進行濾波處理，設Y(f_k)為第k個頻點空域濾波的輸出，則

由于對于頻點f_k，k∈[1,B₁)or(B₂,K]的頻域數據，有w(f_k)＝O_M×1，O_M×1為M×1維的零矢量，所以可以將期望信號帶外部分進行清零處理，降低了運算量和運算復雜度。

第二信號轉換模塊24，用于對濾波后的頻域數據進行傅里葉逆變換，轉換為時域數據并輸出。

其中，可以對空域濾波后的頻域數據Y(f_k)進行K點IFFT(或IDFT)變換，得到抗干擾處理后的時域中頻數據。

如圖4所示，為本發明應用示例的空頻自適應處理器內部處理過程示意圖，該空頻自適應處理器也可稱為頻域寬帶波束形成器。

本應用示例中傅里葉變換采用離散傅里葉變換(DFT)。

寬帶信號可以通過傅里葉變換分為若干個頻點，對于每個頻點按窄帶波束形成的方法進行處理。由K點離散傅里葉變換把寬帶信號在頻域上劃分為K個窄子帶，并對每一個窄子帶進行窄帶波束形成，然后把波束輸出轉化為時域輸出，所以頻域處理是一種劃分子帶的處理方法。如果將一個觀察時間子段的觀察數據進行K點的離散傅立葉變換，可以得到如下的寬帶模型：

X(f_k)＝A(f_k)S(f_k)+N(f_k)k＝1,2,...,K

A(f_k)＝[a(θ₁,f_k)a(θ₂,f_k)...a(θ_N,f_k)]

式中X(f_k)，S(f_k)，N(f_k)分別為對應某頻率的接收數據矢量、信號矢量及噪聲矢量的離散傅立葉變換，K是指將帶寬為B的信號劃分為K個子帶。其中，

X(f_k)＝[x_1k,x_2k,...,x_Mk]^T k＝1,2,...,K

用M×1維向量w(f_k)表示對應于接收數據f_k子帶的處理器權矢量，則

w(f_k)＝[w_1k,w_2k,...,w_Mk]^T k＝1,2,...,K

使用前述所述方法計算w(f_k)，即：

其中，f_k表示第k個頻點，為樣本協方差矩陣，α/β為協方差矩陣修正因子α/β＝γtr(R_k)/M，γ＝1-e^-0.1M，I為單位陣，A為空頻導向矢量，b為N×1維的全1列向量。

則空頻二維處理器的濾波輸出信號為

綜上所述，傳統空域自適應濾波方法很難避免期望信號自相消現象，惡化系統輸出信干噪比，嚴重情況下，常規方法可能完全失效。而本發明實施例利用空頻自適應處理結構，保證多星空頻導向矢量約束，對帶外信號進行清零處理，對帶內信號提出了協方差矩陣修正因子的具體表達式。本發明實施例既簡化工程運算量，又保證多顆衛星信號數據失配時仍能有效地抑制寬帶干擾，增強了空域濾波算法的穩健性。

雖然本發明所揭露的實施方式如上，但所述的內容僅為便于理解本發明而采用的實施方式，并非用以限定本發明。任何本發明所屬領域內的技術人員，在不脫離本發明所揭露的精神和范圍的前提下，可以在實施的形式及細節上進行任何的修改與變化，但本發明的專利保護范圍，仍須以所附的權利要求書所界定的范圍為準。