一種帶噪聲估計器的電池系統荷電狀態估計方法與流程

本發明屬于智能電網中MW級電池儲能系統設計與控制技術領域，涉及一種帶噪聲估計器的電池系統荷電狀態估計方法。

背景技術：

電池系統作為電池儲能系統(BESS)中能量存儲與釋放的主要載體，確定其所含電量的多少不僅是電池管理系統的主要功能之一，且更直接關系著BESS能否有效運行與控制。由于電池充放電過程是一種復雜的電化學反應過程，而電池電量又不易直接由傳感器量測獲得，目前主要用電池荷電狀態(State of Charge,SOC)即電池有效電量與其額定容量的比值來表征電池電量的多少。

傳統的SOC估計方法主要有安時法、開路電壓法和阻抗法等，近年來相繼出現了幾種新型高級算法，如神經網絡法、模糊邏輯法、卡爾曼濾波法及其改進算法等。安時法簡單且易行，在實際應用中得到廣泛采用，但存在誤差累積的局限；針對非線性系統如BESS的SOC估計，常采用擴展卡爾曼濾法(EKF)進行電池SOC估計,但因EKF本身具有需計算雅可比矩陣、忽略高階項等缺點，其估計精度仍存在一定誤差。為此，當前很多學者和專家采用無跡卡爾曼濾波法(UKF)進行電池SOC估計。但是，由于BESS在實際運行中電池系統的噪聲統計信息(如系統噪聲、量測噪聲等)難以獲得或不準確且存在時變性，導致采用UKF進行SOC估計時其估計精度仍受限，因而其SOC估計的精確性仍有待研究改進。

技術實現要素：

本發明解決的問題是在于提供一種帶噪聲估計器的電池系統荷電狀態估計方法，解決電池系統進行SOC估計時采用EKF算法時需計算雅可比矩陣且噪聲統計信息未知或難以獲得而導致估計精度不高、收斂速度慢的問題，從而達到快速、準確估計電池系統SOC的目的。

本發明目的是通過以下技術方案來實現：

本發明提供一種帶噪聲估計器的電池系統荷電狀態估計方法，該電池系統由電池單體通過m串n并而成的m×n型電池系統，其中m、n均為大于1的自然數。

一種帶噪聲估計器的電池系統荷電狀態估計方法如下：首先根據已知電池系統等效電路模型(1)建立電池系統空間狀態方程(2)，再利用噪聲估計器(3)獲得k+1時刻的噪聲估計值(4)，然后以電池系統空間狀態方程(2)中的電池系統荷電狀態SOC_b、2個RC并聯電路的端電壓作為無跡卡爾曼濾波法UKF(5)的狀態變量，以電池系統空間狀態方程(2)的輸入狀態空間方程、輸出電壓狀態空間方程分別作為無跡卡爾曼濾波法UKF(5)的非線性狀態方程f(·)及測量方程g(·)，以k+1時刻的噪聲估計值(4)作為無跡卡爾曼濾波法UKF(5)的噪聲統計信息，采用無跡卡爾曼濾波法UKF(5)得到k+1時刻的中間狀態量(6)，作為下一時刻噪聲估計器(3)的輸入量，同時輸出k+1時刻的電池荷電狀態SOC_b,k+1，以此循環遞推得電池荷電狀態SOC_b估計值。

所述電池系統等效電路模型(1)為二階等效電路模型，模型主電路由2個RC并聯電路、受控電壓源U_b0(SOC)及電池內阻R_b等組成。根據電池系統模型電路結構及其充放電工作特性，等效電路模型的數學表達式為：

式中,a₀～a₅、b₀～b₅、c₀～c₂、d₀～d₂、e₀～e₂、f₀～f₂均為模型系數，可由電池測量數據經擬合而得；Q₀為電池額定電量；SOC₀為SOC初值，一般為0～1的常數；R_s、R_l分別表示電池單體模型中2個RC并聯電路的電阻和C_s、C_l分別表示電池單體模型中2個RC并聯電路的電容；U₀、R分別表示電池單體的開路電壓、內阻；U_b、I_b分別為電池系統端電壓和電流。

所述電池系統空間狀態方程(2)的建立如下：1)、以電池系統SOC_b及2個RC的端電壓U_bs(t)、U_bl(t)作為系統狀態變量x_k，以U_b、I_b分別作為系統量測變量y_k及系統輸入變量，根據等效電路模型建立電池系統空間狀態方程為

式中，U_bs、U_bl為2個RC并聯電路端電壓，τ₁、τ₂為時間常數，Δt為采樣周期，ω_k為系統噪聲，Δt為采樣周期，k為大于1的自然數；2)、根據基爾霍夫電壓定律，結合電池系統等效電路模型，可得電池系統輸出量測方程為：[U_b,k]＝mU_0,k-mR_kI_b,k/n-U_bs,k-U_bl,k+υ_k＝gk(x_k)+υ_k＝y_k，式中，υ_k為系統量測噪聲，k為大于1的自然數。

所述無跡卡爾曼濾波算法UKF(5)的主要步驟為：1)初始化x均值E()和噪聲信息：x₀＝E(x₀)、q₀、Q₀、r₀、R₀；2)計算采樣點x_i,k與對應權重ω：式中，λ＝α²(n+h)-n，n為狀態變量的維數；ω^m、ω^c分別表示方差及均值的權重，算子為對稱陣的Cholesky分解，α、β、h均為常數；3)狀態估計及均方誤差的時間更新：狀態估計時間更新為式中，為狀態方程噪聲均值；均方誤差時間更新為Q_k+1為狀態方程噪聲方差；系統輸出時間更新為式中，g_k-1(·)為測量方程，r_k+1為量測方程噪聲均值；4)計算增益矩陣：式中，P_y,k為自協方差，R_k+1為狀態方程噪聲方差；5)狀態估計及均方誤差的測量更新：狀態估計測量更新為均方誤差測量更新為

所述的噪聲估計器(3)為：式中，K_k+1為增益參數；e_k為列差項，其表達式為y_k為實際測量值；d_k＝(1-b)/(1-b^k+1)，b為遺忘因子，取值范圍為0.95～0.995。

所述的k+1時刻的噪聲估計值(4)有：分別表示k+1時刻的狀態方程噪聲均值估計值、狀態方程噪聲方差估計值、量測方程噪聲均值估計值、量測方程噪聲方差估計值。

所述的k+1時刻的中間狀態量(6)有：P_k+1、e_k+1，分別表示k+1時刻的系統狀態變量估計值、系統輸出變量估計值、噪聲誤差協方差、列差量。

與采用擴展卡爾曼濾波算法(EKF)進行電池系統SOC估計相比，本發明具有以下有益的技術效果：一是整個放電過程，本發明所采用的UKF算法比EKF算法進行電池系統SOC估計時收斂速度更快，魯棒性更好；二是所采用的UKF算法比EKF算法估計精度更高，尤其是放電初期和末期效果更明顯。

附圖說明

圖1為一種帶噪聲估計器的電池系統荷電狀態估計方法流程圖；

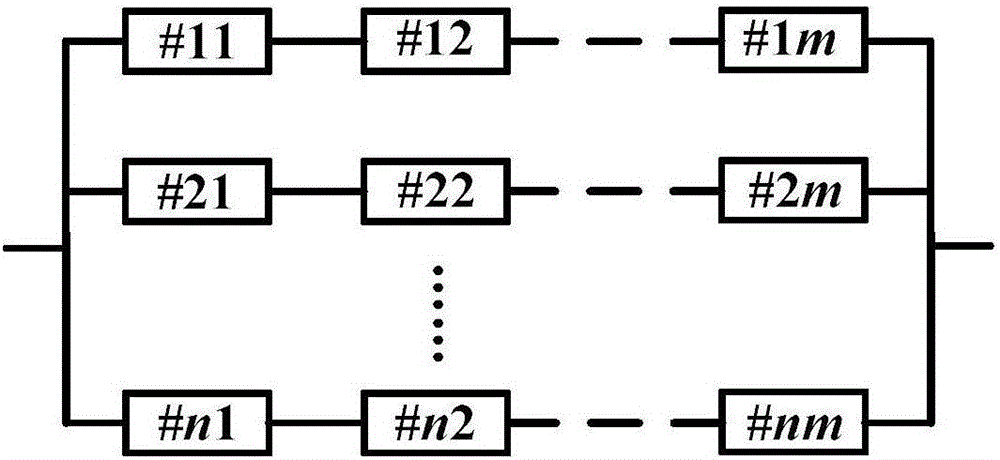
圖2為m×n型電池系統結構示意圖；

圖3為含2個RC并聯電路的電池系統等效電路模型圖；

圖4-1～圖4-2為SOC₀＝0.8時電池恒流放電特性，其中圖4-1為SOC₀＝0.8時SOC變化情況，圖4-2為SOC₀＝0.8時SOC誤差情況。

具體實施方式

下面結合具體的實例對本發明作進一步的詳細說明，所述為對本發明的解釋而不是限定。

根據本發明實施例，如圖1、圖2、圖3和圖4所示，提供了帶噪聲估計器的電池系統荷電狀態估計方法，實施例的流程圖如圖1所示，主要包括以下幾個步驟：

1、確定已知電池系統等效電路模型

1)m×n型電池系統

m×n型電池系統是由多個電池單體經m串n并而成，其結構圖如圖2所示。為便于分析，本實例中假設并聯型電池系統由9個電池單體經3串3并而成，即3×3型電池系統。3×3型電池系統中每個電池單體的額定電壓為3.7V，額定容量為0.86Ah。

2)確定3×3型電池系統等效電路模型

電池系統等效電路模型(1)為二階等效電路模型，模型主電路由2個RC并聯電路、受控電壓源mU₀(SOC)及電池內阻mR/n等組成，如圖3所示。電池系統性能參數通過與電池單體性能參數的關系來獲取，當m＝3、n＝3時，具體電池系統等效電路模型如下：

上式中，a₀～a₅取值分別為-0.915、40.867、3.632、0.537、0.499、0.522，b₀～b₅取值分別為0.1463、30.27、0.1037、0.0584、0.1747、0.1288，c₀～c₂取值分別為0.1063、62.49、0.0437，d₀～d₂取值分別為-200、138、300，e₀～e₂取值分別為0.0712、61.4、0.0288，f₀～f₂取值分別為3083、180、5088。

2、獲取電池系統空間狀態方程

1)、以電池系統SOC_b及2個RC的端電壓U_bs(t)、U_bl(t)作為系統狀態變量x_k，以U_b、I_b分別作為系統量測變量y_k及系統輸入變量，根據等效電路模型建立電池系統空間狀態方程為

式中，U_bs、U_bl為2個RC并聯電路端電壓，τ₁、τ₂為時間常數，Δt為采樣周期，ω_k為系統噪聲，Δt為采樣周期，k為大于1的自然數。

2)、根據基爾霍夫電壓定律，結合電池系統等效電路模型，可得電池系統輸出量測方程為：[U_b,k]＝3U_0,k-R_kI_b,k-U_bs,k-U_b1,k+υ_k＝g_k(x_k)+υ_k＝y_k，式中，υ_k為系統量測噪聲，k為大于1的自然數。

3、利用噪聲估計器結合上一時刻的中間狀態量獲得k+1時刻的噪聲估計值(4)，即式中，K_k+1為增益參數；e_k為列差項，其表達式為y_k為電池系統端電壓測量值；d_k＝(1-b)/(1-b^k+1)，b取值為0.995。

4、將k+1時刻的噪聲估計值(4)分別代替無跡卡爾曼濾波算法UKF(5)的統計信息值(q_k+1、Q_k+1、r_k+1、R_k+1)。

5、利用無跡卡爾曼濾波算法UKF(5)進行電池系統SOC估計，獲取k+1時刻的中間狀態量(6)，即P_k+1、e_k+1。

1)初始化狀態變量x均值E()和噪聲信息：x₀＝E(x₀)＝[1 0 0]、q₀＝0.1、Q₀＝0.3、r₀＝0.01、R₀＝1。2)計算采樣點x_i,k與對應權重ω：

式中，λ＝α²(n+h)-n，n＝3、α取值為1、β取值為2，h取值為0；3)狀態估計及均方誤差的時間更新：狀態估計時間更新為均方誤差時間更新為系統輸出時間更新為4)計算增益矩陣：5)狀態估計及均方誤差的測量更新：狀態估計測量更新為均方誤差測量更新為

最后，將k+1時刻的中間狀態量(6)作為下一時刻噪聲估計器(3)的輸入量，同時，輸出k+1時刻的電池荷電狀態估計值SOC_b,k+1，以此循環遞推從而得不同時刻的電池荷電狀態SOC_b估計值。

系統仿真結果及效果對比

按本一種帶噪聲估計器的電池系統荷電狀態估計方法對3×3型電池系統進行SOC估計，同時采用EKF對此電池系統進行SOC估計，通過仿真結果及實驗數據對比來驗證本一種帶噪聲估計器的電池系統荷電狀態估計方法具有收斂速度快、魯棒性強、精度高的優點。仿真試驗主要恒流工況，即電池以恒流方式(0.8A)向外供電。圖4-1～圖4-2為SOC₀不同時電池恒流放電特性，其中圖4-1為SOC₀＝0.8時SOC變化情況，圖4-2為SOC₀＝0.8時SOC誤差情況。從圖4-1可知，采用自適應UKF(圖中標識為AUKF，下同)與EKF兩種算法進行SOC估計時，兩者均能較好地匹配實驗數據，但由圖4-2可知，放電初始時刻AUKF的誤差更小，驗證了本方法具有更高精度；同時，如圖4-1所示，在初始時刻(20s前)，由于AUKF的噪聲統計信息給定初值不一定為最優，即可能是不準確的值，因此其估計的SOC值偏離實驗數據較大，但在20s時刻后，由于噪聲估計器的濾波作用，其SOC值比EKF算法能更快速地跟蹤實驗數據，兩者收斂時刻分別為20s、40s，驗證了本方法的快速收斂性。