剛體航天器執行器多故障的診斷與容錯控制方法與流程

本發明具體涉及了一種基于觀測器技術的剛體航天器執行器多故障的檢測與容錯控制方法，屬于航空航天飛行控制技術領域。

背景技術：

剛體航天器姿態控制系統是確保航天器能夠正常運行的關鍵部分。由于工作環境的惡劣以及外界存在的各種因素的干擾，使得對于剛體衛星的姿態控制系統的研究顯得更為有必要。正是由于惡劣的工作條件和外界的各類干擾，系統在運行的過程中會不可避免的面臨著來自外界的擾動的影響和自身機構故障造成的嚴重后果的威脅。鑒于剛體航天器姿態控制系統本身在設計過程中存在以下幾方面的難點：首先，復雜的動力學模型和運動學模型為該類航天器控制器的設計與研發帶來了一定程度上的挑戰；其次，由于外界未知擾動的影響、自身存在的嚴重的非線性耦合特性以及快速響應的要求等方面使得航天器控制問題的研究難度進一步增加；最后，由于制造水平、工作成本以及外界環境的約束，航天器執行機構很容易發生不可預測的故障，一旦故障發生，將會給整個計劃造成很嚴重的影響，例如我國于2006發射的地球靜止軌道衛星“鑫諾二號”廣播衛星，由于未按照程序定點在指定位置，導致衛星無法提供正常的通信廣播傳輸服務，造成了巨大的經濟損失。因此，為了保證剛體航天器能夠正常的運行，應該使剛體衛星本身的姿態控制系統對于故障具有一定的自主處理能力。再這樣的基礎之下，以剛體航天器姿態控制系統為基礎的故障檢測與容錯控制研究就顯得很有實際的理論意義和廣泛的應用場合。

目前，針對剛體航天器執行器故障的研究已經取得了比較多的成果。但就當下比較熱門的研究成果來說，仍然存在著以下的一些問題：

(1)在故障檢測方面，由于剛體航天器自身的耦合性造成的各狀態量之間的非線性關系，增加了故障檢測觀測器的設計難度，在已有的一些科研成果中考慮使用了原系統的狀態量來解決觀測器中的非線性項問題，但事實上，根據觀測器的設計定義中觀測器狀態方程中的狀態量應該取自于自身，而不是來自于對象系統，因而這一處理方案還是有待考慮的；

(2)同樣的，還是在故障檢測方面，對于故障的檢測閾值在已有的文獻中，主要還是通過反復仿真實驗的方式，選取觀測狀態值和實際值的最大觀測誤差來獲取故障檢測閾值并且通常情況下這一閾值為一定值，這樣就造成了很大的局限性和保守性，并且容易引起故障的漏報和誤報；

(3)對于容錯控制方案上，很多科研成果著重于通過魯棒控制的方式來解決剛體航天器系統執行器故障，這類容錯控制方案通常被視作作為一種被動式的處理方案。基于這樣的理念所設計的控制器通常同樣也有著很大的局限性和保守性。不僅如此，其所能處理的故障類型和故障值的具體變化情況也多為設計者所預見的類型，對于設計者所未能考慮到的方面，這類容錯控制方案就很難起到原來期望的效果了，甚至有時連基本的穩定要求都難以達到。而本發明能夠很好地解決上面的問題。

技術實現要素：

本發明目的在于針對上面現有技術的不足，提出了一種剛體航天器執行器多故障的診斷與容錯控制方法，該方法針對剛體航天器姿態控制系統執行機構同時發生效率損傷故障和偏差故障的情況下，提供一種能夠針對未知故障進行在線及時檢測和精確估計，并且能夠使得系統能夠具備自主消除故障影響的能力，從而最終實現期望的姿態控制目標的剛體航天器故障診斷與容錯控制。

本發明解決其技術問題所采取的技術方案是：一種剛體航天器執行器多故障的診斷與容錯控制方法，該方法包括如下步驟：

步驟1：建立剛體航天器姿態控制系統的運動學模型和動力學模型，具體如下:

1)剛體航天器控制系統運動學模型：

這里有其中，θ,ψ分別代表滾動角，俯仰角以及偏航角；而ω＝[ω₁,ω₂,ω₃]^T則為剛體航天器基于本體坐標下的角速度向量；ω₀表示已知的常量軌道速度。

考慮到剛體航天器的工作環境，通常情況下σ在一個比較小的范圍內變化，所以，最后剛體航天器姿態小范圍變化下的運動學模型可以表述為：

其中，

2)剛體航天器控制系統動力學模型為：

其中，反對稱矩陣ω^×定義如下：

其中，J為慣量矩陣，u＝[u₁,u₂,u₃]^T表示由三個正交的反作用飛輪提供的控制力矩，d＝[d₁,d₂,d₃]^T為范數有界的未知外界擾動，其滿足‖d‖≤γ，這里γ是一個已知的正常量。

步驟2：建立執行器失效故障和執行器恒偏差故障同時存在的航天器動力學模型，具體如下：

其中，b為執行器效率損傷故障矩陣，b＝diag{b₁,b₂,b₃}，如果b_i＝1，則表示第i個飛輪工作正常，當0＜b_i＜1時，表示執行器出現效率損傷故障，本發明中有0＜b_i≤1。偏差故障向量α＝[α₁,α₂,α₃]^T其具體的值為未知量，通過故障估計觀測器獲取。

步驟3：建立基于自適應閾值技術的故障檢測觀測器，具體如下：

如果存在一個正定對稱矩陣P＝P^T＞0以及一個實矩陣Q，使得如下不等式成立：

Q＝P(Γ-ξJ^-1)+(Γ-ξJ^-1)^TP-2PJ^-1(J^-T)P＞0

則設計具有如下形式的故障檢測觀測器：

其中，為故障檢測觀測器的狀態向量，為觀測器的狀態觀測誤差，當歐拉角以及對應的角速度在一個較小的范圍內變化時，其滿足Lipschitz條件，即為觀測器的增益矩陣。這里定義故障檢測閾值如下：

當觀測誤差的二范數超過時，即檢測到剛體航天器的執行器存在故障。

步驟4：建立自適應故障估計觀測器，具體如下：

注意到原動力學方程中的效率損傷故障矩陣為一對角矩陣，這對于估計執行器效率因子增加了難度，因而這里設B＝[b₁,b₂,b₃]^T和U＝diag{u₁,u₂,u₃}，故可重寫其表述形式如下：

針對如上的動力學方程，設計如下的自適應故障觀測器為：

其中，為故障估計觀測器的狀態向量，為估計的執行器效率因子向量，為估計的執行器偏差故障向量，Σ為自適應故障觀測器的增益矩陣，其為一正定對稱矩陣，且滿足λ_min(Σ)＞ξ||J^-1||。

當中關于和的自適應律具有如下形式：

1)效率損傷故障向量的自適應估計律為：

這里l₁為自適應增益值，其值為一正常量。此外，還有μ₁(0)＞0和υ₁＞0。

2)偏差故障向量的自適應估計律為：

這里l₂同樣為自適應增益值，其值為一正常量，μ₂(0)＞0和υ₂＞0。

步驟5：利用步驟4中估計出的執行器效率因子向量和偏差故障向量來設計反演滑模容錯控制器，首先設z₁＝σ-σ_d為外環跟蹤誤差，z₂＝ω-ω_d為內環跟蹤誤差。進而根據z₁和z₂設計內外環滑模面。考慮到這里的有限時間特性，這里所設計的滑模面中融合了終端滑模控制的思想。相應的滑模面具有如下的形式：

所述控制器參數包括執行器效率因子向量估計值、執行器偏差故障向量估計值、期望的角速度參數、內外環滑模面的誤差量以及外部擾動上界參數。

對于外環，設計虛擬控制器具體如下：

對于內環，設計容錯控制器具體如下：

u＝u₁+u₂

其中，σ為航天器姿態角向量，σ_d為期望的姿態角向量，z₂為內環狀態誤差向量，為內環期望輸入信號，為內環滑模面，和分別為執行器效率因子估計矩陣和執行器偏差故障的估計向量，I_3×1＝[1,1,1]^T，此外，還有a₂，ε₂均為正數，p_i＞q_i＞0,i＝1,2，

有益效果：

1、本發明著眼于剛體航天器執行器同時發生多故障的情形，克服了研究故障類型單一的保守情況。此外，在本發明中還考慮了外界擾動對于系統的影響，因而最后所設計的容錯控制方案較之前的一些成果在故障檢測和容錯控制方面更具有實際工程意義。

2、關于故障檢測部分，不同于已有的很多方案中所采用的保守性的閾值選擇方法，本發明采用了自適應閾值方法，通過變化的閾值來對故障是否發生進行實時在線檢測，從而減少了故障誤報或漏報的可能性。

3、在故障估計部分，本方案中所采用的方法可以保證故障估計誤差是漸進收斂的，這一點較很多文獻中所說的估計誤差滿足最終一致有界條件要更為嚴格，從側面說明了本方案對于故障的估計是可靠的、有效的。

4、基于已知的故障信息，本方案中的容錯控制策略結合反演控制理念設計了相應的容錯控制器。這里值得注意的是，由于在容錯控制器中還運用了積分終端滑模技術，這就使得系統在該容錯控制器的作用下，可以在有限時間內達到容錯控制目的。

5、本發明的故障診斷模塊、故障估計模塊的設計是相對獨立的，這也保證了各自的工作狀態是相對獨立的，使得設計過程相對來說變得更加容易，從而保證了在工程上的實際應用的可能。

附圖說明

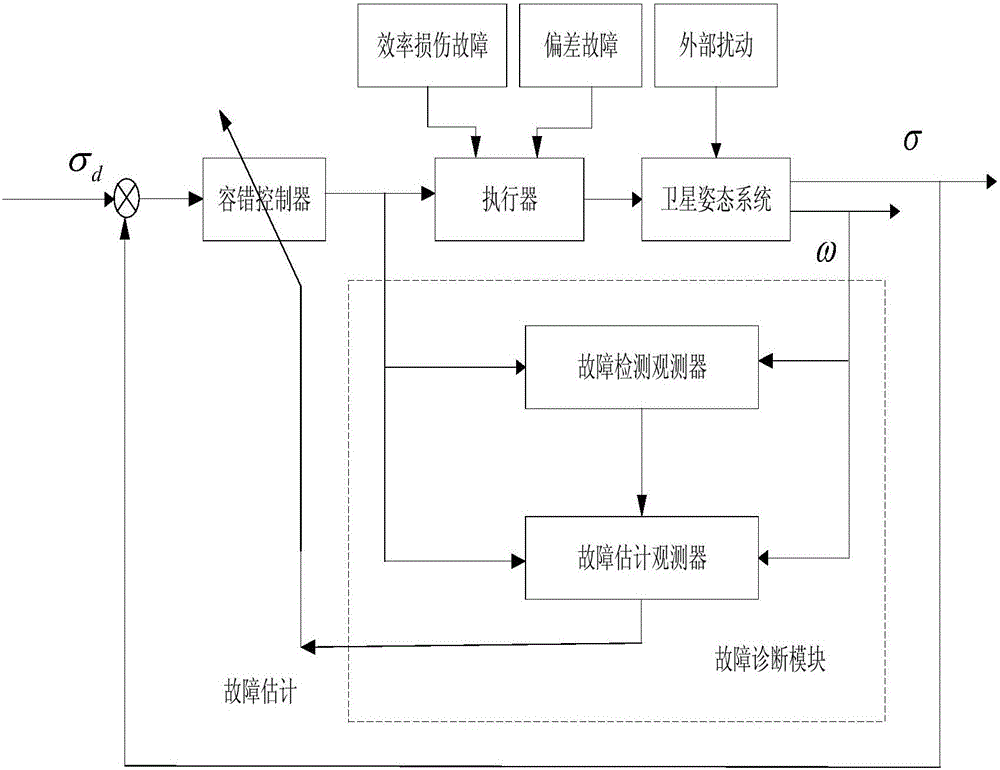
圖1是本發明的故障檢測、故障估計以及容錯控制方法的結構框圖。

圖2(a)是無故障情況下剛體航天器姿態角響應曲線，圖2(b)是剛體航天器發生偏差故障和效率損傷故障情況下的姿態角響應曲線圖。

圖3是故障檢測觀測器的閾值檢測曲線圖。

圖4(a)是執行器偏差故障的實際值和估計曲線圖，圖4(b)是執行器效率損傷故障下的有效因子的實際值和估計值曲線。

圖5是同時發生偏差故障和效率損傷故障時，使用本發明中容錯控制策略時的姿態角響應曲線圖。

具體實施方式

下面結合說明書附圖對本發明創造作進一步的詳細說明。

現結合圖1來具體闡述本發明的具體內容，并在最后通過Matlab仿真來驗證本發明的實際容錯控制效果。如圖1所示，當剛體航天器執行機構同時發生效率損傷故障和偏差故障時，為使剛體航天器能夠跟蹤上期望的姿態，通過故障檢測觀測器和故障估計觀測器來對故障的信息進行精確的估計。進而在已知故障信息的基礎上設計反演終端滑模容錯控制器，從而提高了剛體航天器姿態系統對于故障的容忍能力。

本發明測器技術的剛體航天器故障檢測與容錯控制方法，包括以下步驟：

步驟1：建立剛體航天器姿態控制系統的運動學模型和動力學模型，具體如下:

1)剛體航天器控制系統運動學模型：

這里有其中，θ,ψ分別代表滾動角，俯仰角以及偏航角；而ω＝[ω₁,ω₂,ω₃]^T則為剛體航天器基于本體坐標下的角速度向量；ω₀表示已知的常量軌道速度。

考慮到剛體航天器的工作環境，通常情況下σ在一個比較小的范圍內變化，所以，最后剛體航天器姿態小范圍變化下的運動學模型可以簡化表述為：

其中，

2)剛體航天器控制系統動力學模型為：

其中，反對稱矩陣ω^×定義如下：

其中，J為慣量矩陣，u＝[u₁,u₂,u₃]^T表示由三個正交的反作用飛輪提供的控制力矩，d＝[d₁,d₂,d₃]^T為范數有界的未知外界擾動，其滿足‖d‖≤γ，這里γ是一個已知的正常量。

步驟2：建立執行器失效故障和執行器恒偏差故障同時存在的航天器動力學模型，具體如下：

其中，b為執行器效率因子矩陣，b＝diag{b₁,b₂,b₃}，如果b_i＝1，則表示第i個飛輪工作正常，當0＜b_i＜1時，表示執行器出現效率損傷故障，本發明中有0＜b_i≤1。偏差故障向量α＝[α₁,α₂,α₃]^T其具體的值為未知量，通過故障估計觀測器獲取。

步驟3：建立基于自適應閾值技術的故障檢測觀測器，具體如下：

如果存在一個正定對稱矩陣P＝P^T＞0以及一個實矩陣Q，使得如下不等式成立：

Q＝P(Γ-ξJ^-1)+(Γ-ξJ^-1)^TP-2PJ^-1(J^-T)P＞0

則設計具有如下形式的故障檢測觀測器：

其中，為故障檢測觀測器的狀態向量，為觀測器的狀態觀測誤差，當歐拉角以及對應的角速度在一個較小的范圍內變化時，其滿足Lipschitz條件，即為觀測器的增益矩陣。這里定義故障檢測閾值如下：

當觀測誤差的二范數超過時，即檢測到剛體航天器的執行器存在故障。

接下來，利用Lyapunov穩定性理論，設計Lyapunov函數證明故障檢測觀測器的穩定性：

其中P為正定對稱矩陣，為觀測器的狀態觀測誤差。結果證明利用步驟三所設計的故障檢測觀測器是穩定的，并且能夠證明得到當觀測誤差的二范數超過時，即檢測到剛體航天器的執行器存在故障。值得強調的是，不同于一些已經存在的工作，這里的故障檢測閾值是變化的。這樣就有效的提高了故障檢測的準確率，降低了誤報和漏報的可能性。

步驟4：建立自適應故障估計觀測器，具體如下：

考慮到很多已有工作中，在設計自適應故障估計觀測器時，其最終結果只能得到最終一致有界的效果，這一點對于實際的應用來說是不夠的。下面設計的自適應故障估計觀測器能夠保證所得的結果是漸進穩定的，從而克服了上面所說的問題。

注意到原動力學方程中的效率因子矩陣為一對角矩陣，這對于估計執行器效率因子增加了難度。因而這里考慮對其形式進行一定的修改，設B＝[b₁,b₂,b₃]^T和U＝diag{u₁,u₂,u₃}，故可重寫其表述形式如下：

針對如上的動力學方程，設計如下的自適應故障觀測器：

其中，為故障估計觀測器的狀態向量，為估計的執行器效率因子向量，為估計的執行器偏差故障向量，Σ為自適應故障觀測器的增益矩陣，其為一正定對稱矩陣，且滿足λ_min(Σ)＞ξ||J^-1||。

當中關于和的自適應律具有如下形式：

1)效率損傷故障向量的自適應估計律為：

這里l₁為自適應增益值，其值為一正常量。此外，還有μ₁(0)＞0和υ₁＞0。

2)偏差故障向量的自適應估計律為：

這里l₂同樣為自適應增益值，其值為一正常量，μ₂(0)＞0和υ₂＞0。

接下來，利用Lyapunov穩定性理論，設計Lyapunov函數證明所設計的自適應故障估計觀測器是

其中，為觀測器的狀態觀測誤差，為效率因子向量和估計的效率因子向量之間的誤差，為偏差故障向量和估計的偏差故障向量之間的誤差。結果證明所設計的自適應故障估計觀測器是穩定的，并且其對于故障估計的誤差可以滿足漸進穩定要求。

步驟5：利用步驟4中估計出的執行器效率因子向量和偏差故障向量來設計反演滑模容錯控制器，首先設z₁＝σ-σ_d為外環跟蹤誤差，z₂＝ω-ω_d為內環跟蹤誤差。進而根據z₁和z₂設計內外環滑模面。考慮到這里的有限時間特性，這里所設計的滑模面中融合了終端滑模控制的思想。相應的滑模面具有如下的形式：

所述控制器參數包括執行器效率因子向量估計值、執行器偏差故障向量估計值、期望的角速度參數、內外環滑模面的誤差量以及外部擾動上界參數。對于外環，設計虛擬控制器具體如下：

對于內環，設計容錯控制器具體如下：

u＝u₁+u₂

其中，σ為航天器姿態角向量，σ_d為期望的姿態角向量，z₂為內環狀態誤差向量，為內環期望輸入信號，為內環滑模面，和分別為執行器效率因子估計矩陣和執行器偏差故障的估計向量，I_3×1＝[1,1,1]^T，此外，還有a₂，ε₂均為正數，p_i＞q_i＞0,i＝1,2，

進而，利用Lyapunov穩定性理論，設計Lyapunov函數證明系統全局的有限時間穩定性：

結果證明：依據步驟4中所得到的效率因子向量和偏差故障向量，這里所設計的容錯控制器可以保證故障下的剛體航天器可以在有限時間內達到期望的姿態。

本發明利用Matlab2015a軟件，對所發明的容錯控制方案進行了仿真驗證，具體包括：

(1)剛體航天器姿態控制系統參數選取：

剛體航天器系統總慣性矩陣外部擾動矩陣為k₁＝1.2，p₁＝p₂＝5，k₁＝1.2，k₂＝3.8，ε₁＝ε₂＝0.1，a₁＝1,a₂＝2，Γ＝diag{3,3,3}，Σ＝diag{4,4,4},q₁＝q₂＝3。

(2)初始參數選取：

軌道速度ω_o＝0.15deg/s，跟蹤信號：σ_d＝[1,2,3]^T deg，姿態角初始條件：σ₀＝[0.3,0.2,-0.3]^T deg，姿態角速率初始條件：ω₀＝[0.05,0.06,-0.04]^T deg/s，

(3)執行器故障參數選取如下：

執行器效率因子為執行器偏差故障向量

結果說明：

在圖2(a)中，這里給出了在無故障情況下的剛體航天器姿態角響應曲線。在圖2(b)中，這里給出了在第2秒時，剛體航天器執行器同時發生效率損傷故障和偏差故障的姿態角響應曲線。可以明顯的看出，當剛體航天器執行器同時發生效率損傷和偏差故障時，其響應曲線的動態性能是很不理想的，甚至自身的穩定性都難以維持，在這樣的情況下，要求其跟蹤上目標信號顯得不切實際；

在圖3中，由于引入了故障檢測觀測器，使得系統可以及時對所發生的故障進行處理，圖中在第2秒時，系統殘差信號超越了自適應閾值，故障檢測觀測器在發出故障警報的同時，激發故障估計觀測器對故障具體值進行自適應估計。

根據設計的自適應律，故障估計觀測器在圖4(a)和圖4(b)中分別給出了剛體航天器效率因子向量的估計值和偏差故障的估計值，這里要指出的是由于原效率因子矩陣為對角陣，所以可以很容易的由向呂因子向量求解出效率因子矩陣。

圖5為在同時發生執行器效率損傷故障和偏差故障的情況下的姿態角相應出現，這里注意到剛體航天器利用本發明中的容錯控制策略可以在8s的時間內進行故障補償并保證系統的穩定性。

由此可知：針對剛體航天器同時發生執行器效率損傷故障和偏差故障的情況，本發明所提出的一種基于觀測器技術的故障檢錯與容錯控制方案能夠較好的在線實時精確的對故障進行檢測和估計，從而提高了剛體航天器姿態系統對于故障的容忍能力。

本發明未詳細說明部分都屬于本領域技術人員所公知知識，以上所述為本發明的一個具體實施案例，這里并不限制本發明的應用場合，凡在本發明的精神和原則內，所做的任何修改、等同替換或改進等，均應包含在本發明的保護范圍內。