一種擴散加權成像方法與流程

【技術領域】

本發明涉及磁共振成像技術領域，尤其涉及一種體素內非相干運動擴散加權成像方法。

背景技術：

擴散加權成像(diffusionweightedimaging，dwi)屬于功能影像學的范疇，是目前唯一在體測量組織內水分子擴散運動的成像方法，其成像的原理是利用水分子的布朗運動，無需注射對比劑即可其反應人體組織的微觀結構以及細胞內外水分子的轉移與跨膜運動、溫度等的變化。通過dwi圖像信號高低的定性比較及表觀擴散系數(apparentdiffusioncoefficient，adc)的定量測量對組織結構及功能變化進行評估，可用于顯示疾病的敏感性以及診斷和鑒別診斷等方面。

在傳統擴散理論中，水分子在一定時間內從某一部位擴散到另一部位的位移運動呈高斯分布，dwi影響信號隨著b值的增加呈單指數函數衰減。然而，由于細胞膜、細胞內外間隔等擴散障礙物的影響使生物組織中水分子的擴散比自由水的擴散復雜，組織中水分子的位移偏離高斯分布。另外，基于多b值dwi研究發現，dwi信號隨b值增大并不遵循單指數遞減規律。dwi影像上信號衰減同時包括真性水分子擴散和毛細血管網中隨機血流微循環灌注，后者使擴散影像上出現假擴散信號，導致adc值反應的信息有限，這種現象即為體素內非相干運動(intravoxelincoherentmotionimaging，ivim)。基于ivim雙指數模型的dwi是采用多個b值的掃描成像，可以分離出組織的真實擴散 信息和微循環灌注信息。lebihan等^[1]首次將ivim-dwi應用于臨床，主要用于將水分子擴散與毛細血管微循環灌注區分開，不僅對神經系統，而且對其他各部位的多種生理和病例機制都能提供定量指標，成為廣泛關注的新興成像熱點。

但是ivim參數成像的一個常見問題是圖像的較弱信噪比導致的參數估計的可靠性較差。傳統方法多采用高斯方法去噪，但是dwi中噪聲主要成像rician(萊斯)分布，因此基于高斯噪聲的去噪方法容易產生誤差。此外，還存在各種改進ivim成像參數可靠性的方法，如加權均值濾波、線性最小均方誤差、非局部均值濾波等。然而這些方法有些需要額外的數據采樣平均，還有些需要復雜的計算方法，在實際應用中都有一定的局限性。基于此，有必要對現有ivim-dwi成像方法進行改進，在去除噪聲的同時改善ivim成像參數的可靠性。

[1]、lebihand,bretone,lallemandd,etal.separationofdiffusionandperfusioninintravoxelincoherentmotionmrimaging[j].radiology,1988,168(2):497-505.

技術實現要素：

本發明所要解決的技術問題是提出一種可提高體素內非相干運動擴散加權成像中ivim參數估計可靠性的方法。

本發明解決上述技術問題所采用的技術方案為一種擴散加權成像方法，包括如下步驟：

利用磁共振掃描儀采集受檢者多個b值dwi圖像；

采用基于svd-pca的方法對所述dwi圖像進行降噪處理，獲取降噪處 理后的dwi圖像；

對所述降噪處理后的dwi圖像進行非線性擬合，獲得體素內非相干運動的參數估計，所述參數包括真性擴散系數、假性擴散系數和灌注分數。

進一步地，所述采用基于svd-pca的方法對所述dwi圖像進行降噪處理的具體過程為：

將所述dwi圖像分解成若干個圖像塊，相鄰圖像塊之間存在重疊部分；

將所述圖像塊展成矢量組成矢量合成矩陣；

對所述矢量合成矩陣進行奇異值分解，獲取所述矢量合成矩陣中各基矢量的分量值；

根據設定閾值對所述分量值進行過濾處理獲取去噪后的合成矩陣，并對去噪后的合成矩陣作svd反變換獲取去噪后的dwi圖像。

進一步地，還包括對相鄰圖像塊之間重疊部分所展成的矢量作均值處理。

進一步地，對所有b值dwi圖像的每個b值dwi圖像分別進行降噪處理，且每個b值dwi圖像都有對應的矢量合成矩陣。

進一步地，對所有b值dwi圖像中的至少兩個同時進行降噪處理，且同一b值dwi圖像的不同圖像塊展成的矢量對應矢量合成矩陣的不同行，不同b值dwi圖像中相同位置的圖像塊展成的矢量對應矢量合成矩陣的同一行。

進一步地，所述根據設定閾值對所述分量值進行過濾處理的具體過程為：對小于設定閾值的分量值作置零處理，并保留大于或等于設定閾值的分量值。

進一步地，所述設定閾值通過如下方式獲得：

分別采用不同閾值對各分量值進行過濾處理，得到不同閾值對應的合成矩陣；

對不同閾值對應的合成矩陣作svd反變換獲得不同閾值所對應的dwi重 建圖像；

計算不同閾值所對應的dwi重建圖像間的均方差并獲取均方差曲線，所述設定閾值為所述均方差曲線上峰值位置后端所對應的閾值。

進一步地，采用levenberg-marquardt對所述降噪處理后的dwi圖像進行非線性擬合獲取計算參數值，并根據所述計算參數值獲取參數估計值。

進一步地，所述參數估計的值為所述計算參數值的平方。

進一步地，根據高b值dwi圖像估計所述真性擴散系數，根據全部b值dwi圖像估計所述假性擴散系數和灌注分數。

與現有技術相比，本發明的優點在于：在對多個b值dwi圖像進行非線性擬合前，采用基于svd-pca的方法將多個b值dwi圖像展成矢量合成矩陣，通過對矢量合成矩陣的奇異值進行過濾處理可有效去除dwi圖像的噪聲成分，提高信噪比，進而提高體素內非相干運動參數估計的可靠性；在采用levenberg-marquardt對所述降噪處理后的dwi圖像進行非線性擬合的過程中，將估計參數采用變量平方替換，保證所有參數估計的非負性，參數估計可靠性進一步提高。

【附圖說明】

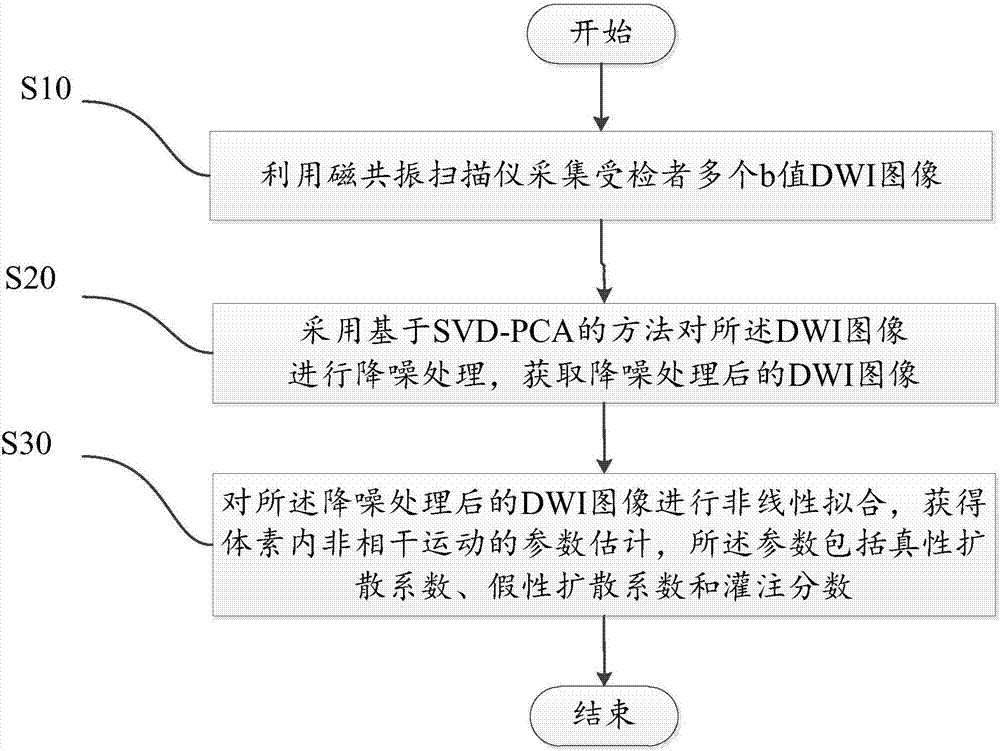
圖1為本發明的擴散加權成像方法流程圖；

圖2為本發明施加的擴散敏感梯度場示意圖；

圖3為本發明實施例一不同閾值所對應的重建圖像間的均方差曲線示意圖；

圖4為本發明dwi成像方法獲得假性擴散系數圖；

圖5為本發明dwi成像方法獲得的真性擴散系數圖；

圖6為本發明dwi成像方法獲得的灌注分數圖。

【具體實施方式】

為使本發明的上述目的、特征和優點能夠更為明顯易懂，下面結合附圖和實施例對本發明的具體實施方式做詳細的說明。

如圖1所示，本發明的擴散加權成像方法主要包括：

s10、利用磁共振掃描儀采集受檢者的多個b值dwi圖像。水分子在介質中的隨機運動稱為擴散，當梯度磁場存在時，水分子的擴散引起橫向磁化矢量的失相位，引起mr信號降低。dwi可以觀察水分子的擴散特性，為增加擴散的敏感性，需施加擴散敏感梯度，施加的擴散敏感梯度可與自旋回波(spinecho，se)、平面回波成像(echoplanarimaging，epi)、快速自旋回波(fastspinecho，fse)、梯度回波序列(gradientechopulsesequence，gre)等脈沖序列融合，并可顯著增加脈沖序列對水分子布朗運動的敏感性。擴散梯度包含兩個擴散敏感梯度場，如圖2所示在se序列基礎上，兩個極性和大小均相同的擴散敏感梯度場位于180°脈沖的兩側對稱位置。對于彌散速度慢的水分子，第一個梯度脈沖所致的質子自旋去相位會被第二個梯度脈沖再聚集，信號不降低；而對于彌散速度快的水分子，第一個梯度脈沖所致的質子自旋去相位離開了原來的位置，不能被第二個梯度脈沖再聚集，信號降低，從而形成dwi上的信號差別。彌散加權的程度用彌散敏感因子b表示，代表彌散敏感梯度場強的大小，而dwi是在某一b值下測得的信號強度成像，其中，b值的物理計算公式為：b＝γ²g²δ²(δ-δ/3)，其中，γ為磁旋比，g、δ、δ分別代表施加的兩個擴散敏感梯度場的幅度、持續時間及間隔時間。本實施例中，在梯度方向上施加彌散梯度，獲取b值分別為b0＝0s/mm²，b1＝10s/mm²，b2＝20s/mm²，b3＝40s/mm²， b4＝60s/mm²，b5＝80s/mm²，b6＝110s/mm²，b7＝140s/mm²，b8＝170s/mm²，b9＝200s/mm²，b10＝300s/mm²，b11＝400s/mm²，b12＝500s/mm²，b13＝600s/mm²，b14＝700s/mm²，b15＝800s/mm²，b16＝900s/mm²，b17＝1000s/mm²等18個不同的彌散敏感因子在受檢者腦部的dwi圖像。

需要說明的是：當施加擴散敏感梯度時，b值越高，dwi對于水分子的運動越敏感，但組織信號衰減也越明顯，過高的b值得到的dwi信噪比(snr)很低；在機器硬件條件一定的情況下，b值增高必然會延長回波時間，從而進一步降低snr。較小的b值得到的圖像信噪比高，但是對水分子擴散運動的檢測不敏感，而且組織信號的衰減受諸如組織血液灌注中水分子運動、各種生理運動、細胞本身結構、組織特性、溫度等各種因素的影響，這些運動模式相對于水分子的擴散運動來說要明顯得多。因此本發明采用雙指數模型來分析不同b值下dwi信號衰減的規律。由ivim理論：

sb/s0＝(1-f)·exp(-bd)+f·exp[-b(d+d^*)](1)

其中，s代表體素內的信號強度；d代表體素內真性水分子擴散，稱為真性擴散系數；d*代表體素內微循環灌注，稱為假性擴散系數(pseudodiffusioncoefficient)；f表示灌注分數(perfusionfraction)，代表體素內微循環灌注效應占總體擴散效應的容積率。需要說明的是，本實施例中，無需對所有dwi圖像進行數據采樣平均，對于dwi圖像可進行一定的預處理：對圖像進行合理的重采集以及配準，實現數據的優化；利用四鄰域方法對優化后的圖像進行平滑，以消弱圖像中極值的影響。

s20、采用基于奇異值分解(singularvaluedecomposition，svd)與主成分分析(principalcomponentanalysis，pca)的方法對上述dwi圖像進行降噪處理，獲取降噪處理后的dwi圖像。在本發明一實施例中，分別對每個b 值dwi圖像采用基于奇異值分解與主成分分析svd-pca的方法進行降噪處理，具體過程包括：

(a)將任一b值dwi圖像分解成若干個圖像塊，其中相鄰圖像塊之間存在重疊的部分。在本實施例中，以b0值dwi圖像為例說明：采用滑動窗口對該dwi圖像作有重疊的分塊分解，每次窗口滑動都會在窗口包含的圖像區域產生一個圖像塊，且窗口滑動不存在跳躍的現象，這樣分解產生的相鄰圖像塊之間存在部分重疊，最終單個dwi圖像會形成m個小圖像塊。需要說明的是，對于相鄰圖像塊重疊的部分，可進行均值處理，重疊區域的圖像像素值為兩次窗口滑動采集的平均值或者加權處理后的均值，有利于消除窗口滑動產生的塊效應。

(b)將所有圖像塊展成(轉換或者轉化成)矢量組成矢量合成矩陣。各個圖像塊由同一窗口滑動分解獲得，因此各個圖像塊包含的像素點的數目相同，每個圖像塊展成或者轉化為矢量后的元素數也相同。設第一個圖像塊轉化的矢量為{a11，a12，a13，…，a1n}，第2個圖像塊轉化的矢量為{a21，a22，a23，…，a2n}，則第m個圖像塊轉化的矢量為{am1，am2，am3，…，amn}。以其中一個圖像塊轉化的矢量作為矢量合成矩陣的行，則該dwi的所有圖像塊轉化的矢量可組成m×n的矢量合成矩陣c，矢量合成矩陣的行數等于該dwi圖像分解的圖像塊數，即矢量合成矩陣是m個n維向量，m>n。

(c)對矢量合成矩陣作奇異值分解，獲取矢量合成矩陣中各基矢量的分量值。對于矢量合成矩陣c作svd，可寫成c＝u*s*v^t(即矢量合成矩陣c可分解為三個矩陣之積)，其中u為m×m的矩陣，u的列是cc^t的正交特征向量；v為n×n的矩陣，v的列是c^tc的正交特征向量；s為m×n的奇異值矩陣，且s為對角矩陣，對角元素為從大到小排列的特征值，也可稱為矢量 合成矩陣中各基矢量的分量值。更詳細地，s是矢量合成矩陣c的奇異值構成的對角矩陣，s＝diag(λ1，λ2，…λi…，λp)，其中,λi為矢量合成矩陣c的奇異值，λ1≥λ2≥…≥λi…≥λp，且p<n。

在上述svd分解過程中，可以認為(u、v)是一組正交變換基對，而奇異值則是變換系數。大的奇異值對應圖像塊在變換域中的低頻部分，小的奇異值對應著圖像塊在變換域中的高頻部分。在圖像中，高頻部分對應著圖像紋理細節和噪聲。通過設定一個合適的閾值，濾除較小的奇異值，保留較大的奇異值，則可起到去噪的結果。

(d)根據設定閾值對分量值進行過濾處理獲取去噪后的合成矩陣，并對去噪后的合成矩陣作svd反變換獲取去噪后的dwi圖像。在本發明實施例中，分別采用不同閾值對各分量值進行過濾處理，重建合成矩陣，其中對大于或等于閾值的分量值保留，對小于閾值的分量作置零處理；根據不同閾值對應的合成矩陣作svd反變換，獲得不同閾值所對應的dwi重建圖像；計算不同閾值所對應的重建圖像間的均方差并獲取均方差曲線；在均方差曲線上出現峰值位置的前端所對應的閾值選定為設定閾值。如圖3所示為本實施例中獲得的均方差曲線，其中橫坐標表示經過過濾處理的合成矩陣中非零奇異值的個數，縱坐標表示對應合成矩陣反變換后得到的dwi重建圖像間的均方差，從圖可看出，當合成矩陣的非零奇異值個數在7-11之間變化時，dwi重建圖像間的均方差在45-60之間波動，說明dwi重建圖像的內容基本沒有變化；當合成矩陣的非零奇異值個數減小到6個時，dwi重建圖像間的均方差處于峰值或最大峰值(本實施例中約為130)，遠高于合成矩陣的非零奇異值個數為7時的均方差。因此，在本實施例中，選定均方差曲線上峰值或最大峰值位置后端所對應的閾值即第7個非零奇異值為設定閾值。在通過上述過程獲得設定閾值后，對 經過奇異值分解的基矢量的各個分量值進行去噪處理，其中：對小于設定閾值的分量作置零處理，并保留大于或等于設定閾值的分量。按照上述過程可獲得所有b值dwi圖像去噪處理后的圖像。

s30、對降噪處理后的dwi圖像進行非線性擬合，獲得體素內非相干運動的參數估計，其中參數估計包括d真性擴散系數估計、d*假性擴散系數估計和f灌注分數估計。由于d*值顯著大于d值，常高于d值數十個數量級，因此，應用低b值dwi(通常指b<200s/mm²)測量到的信號衰減主要反映灌注效應，高b值dwi(b＝200-1000s/mm²)測量到的信號衰減主要反映水分子擴散。根據上述分析，在本發明一實施例中，采用levenberg-marquardt對所述降噪處理后的dwi圖像進行分段非線性擬合，其中采用高b值dwi圖像估計真性擴散系數，采用全部b值dwi圖像估計假性擴散系數和灌注分數。需要說明的是：為保證保證所有參數圖的非負性，本實施例中采用變量代換，即令d*＝(d*)²,d＝(d)²,f＝(f)²，采用levenberg-marquardt對d*,d和f進行非線性擬合，從而確保d*圖，d圖，以及f圖都是正值，其中d*、d、f分別是代換變量。

單獨的噪聲圖像塊信息有限，對其進行處理不能很好的將信號從噪聲中分離出來。本發明的擴散加權成像方法，在采用svd-pca的方法對dwi圖像進行降噪處理時，可將所有b值dwi圖像分為若干組，每組至少包含兩個不同b值dwi圖像，對每組的dwi圖像進行滑動窗口分解為多個圖像塊，且屬于同一組的圖像塊經矢量轉換后共同組成矢量合成矩陣，采用如實施例一類似的方法對每組的矢量合成矩陣進行去噪處理。需要說明的是，在每組的矢量合成矩陣中，屬于同一個b值dwi圖像的不同圖像塊展成的矢量對應矢量合成矩陣的不同行，不同b值dwi圖像中相同位置的圖像塊展成的矢量串接對應 矢量合成矩陣的同一行。為有效去除噪聲的干擾，在本發明實施例二中，采用基于奇異值分解與主成分分析svd-pca的方法對上述dwi圖像進行降噪處理，獲取降噪處理后的dwi圖像具體步驟為：

(a)將所有b值dwi圖像分解成若干個圖像塊，其中相鄰圖像塊之間存在重疊的部分。在本實施例中，采用滑動窗口分別對b0-b17等18個b值dwi圖像作有重疊的分塊分解，每次窗口滑動都會在窗口包含的圖像區域產生一個圖像塊，且窗口滑動不存在跳躍的現象，這樣分解產生的相鄰圖像塊之間存在部分重疊，本實施例中每個b值dwi圖像會形成m個圖像塊。需要說明的是，對于相鄰圖像塊重疊的部分，可進行均值處理，重疊區域的圖像像素值為兩次窗口滑動采集的平均值或者加權處理后的均值，有利于消除窗口滑動產生的塊效應。

(b)將所有圖像塊展成矢量組成矢量合成矩陣。所有b值dwi的圖像塊由同一窗口滑動分解獲得，因此各個圖像塊包含的像素點的數目相同，每個圖像塊轉化為矢量后的元素數也相同。與實施例一不同之處在于：對于同一b值dwi圖像，不同圖像塊轉化的矢量分布在矢量合成矩陣的不同行；對于不同b值dwi圖像，屬于同一滑動窗口的對應圖像塊轉化成的矢量串接在矢量合成矩陣的同一行。如b0值dwi圖像由窗口滑動形成的第一圖像塊轉化為矢量{a11，a12，a13，a14}，b1值dwi圖像由窗口滑動形成的第一圖像塊轉化為矢量{b11，b12，b13，b14}，依次類推bx(bx≤b17)值dwi圖像由窗口滑動形成的第一圖像塊轉化為矢量{x11，x12，x13，x14}，則矢量合成矩陣的第一行可表示為{a11，a12，a13，a14，b11，b12，b13，b14，…，x11，x12，x13，x14，…}。對于合成矩陣作奇異值分解獲取各基矢量的分量值，以及根據設定閾值對分量值進行過濾處理獲取去噪后的合成矩陣具體方法可參考實施例一。

作為對比，本發明在實施例三中對利用磁共振掃描儀采集的受檢者多b值dwi圖像未采用降噪處理，且所有b值dwi圖像都沒有做采樣平均，而直接levenberg-marquardt方法進行非線性擬合獲取計算參數值，且各參數估計值為計算參數值的平方。如圖4為采用本發明dwi成像方法獲得的假性擴散系數圖，其中圖4a對應實施例一，圖4b對應實施例二，圖4c對應實施例三，不同灰度值代表不同的信號估計強度，采用svd-pca進行去噪處理獲取的假性擴散系數圖中孤立點或估計錯誤點(圖中亮度值較高的白點)的個數明顯少于僅采用levenberg-marquardt方法獲得的假性擴散系數圖，說明采用svd-pca進行前期處理可明顯提高假性擴散系數估計的正確率。此外，dwi圖像噪聲不僅導致圖像在空間的波動，也導致同一像素在b值分布方向的的波動，因此看出對每個b值dwi圖像單獨去噪與對所有b值dwi合成矩陣作去噪效果是不一樣的，且對所有b值dwi合成矩陣采用svd-pca獲得的假性擴散系數圖中出現孤立點的個數更少，去噪的效果更好，假性擴散系數估計的正確率更高。如圖5為采用本發明dwi成像方法獲得的真性擴散系數圖，其中圖5a對應實施例一，圖5b對應實施例二，圖5c對應實施例三，由于本發明在利用levenberg-marquardt進行參數擬合過程中采用了變量替換，保證了所有參數的非負性，無論是否采用svd-pca進行去噪處理，真性擴散系數圖都僅有部分孤立點或估計錯誤點。更進一步地，與圖5c相比，圖5a中采用svd-pca進行前期處理進一步提高了真性擴散系數估計的正確率。如圖6為采用本發明dwi成像方法獲得的灌注分數圖，其中圖6a對應實施例一，圖6b對應實施例二，圖6c對應實施例三。對比圖6a和圖6c，所有b值dwi合成矩陣采用svd-pca進行去噪處理獲取的灌注分數圖中孤立點或估計錯誤點(圖中亮度較高的白點)的個數明顯少于僅采用levenberg-marquardt方法獲得的灌注 分數圖。對比圖6a與圖6b，對每個b值dwi圖像單獨去噪獲取的灌注分數圖中孤立點或估計錯誤點的個數，ivim參數估計的可靠性明顯提高。

以上所述僅為本發明的較佳實施例而已，并不用以限制本發明，凡在本發明的精神和原則之內，所做的任何修改、等同替換、改進等，均應包含在本發明的保護范圍之內。