組合受荷樁承載力傳遞矩陣通解方法與流程

本發明涉及一種組合受荷樁承載力傳遞矩陣通解方法。

背景技術：

樁基礎一開始以承擔上部結構豎向承載力為主要設計目的，隨著工程需求的變化，出現了以承擔水平荷載作用為主的水平受荷樁。然而，隨著對基樁承載特性的研究的深入和理論的逐步完善，發現實際工程中的樁基通常不但承擔樁頂豎向荷載作用，還同時受到水平荷載作用，即組合荷載的作用，如橋梁樁基礎，海上風機單樁基礎等。

組合荷載下水平力使樁身產生較大內力和位移，豎向分力也因樁身撓曲變形而產生附加彎矩，尤其是當地基土質較差、地面以上樁自由長度較大時，附加的樁身撓曲變形和彎矩更不可忽略，即所謂的P-Δ效應，因此組合荷載作用下基樁承載特性越來越受到重視。大量的學者開展了眾多關于組合受荷樁承載特性的離心模型實驗研究、室內模型試驗研究以及二維、三維有限元數值模擬研究并得出諸多有益的結論。然而，這些研究成果只能反映特定情況下的樁身響應特性，且一般情況下這些研究成果反映的是承載特性定性結論，并不能為實際的工程設計人員提供很好的設計依據。因此，組合受荷樁樁身響應的解析模型的建立以及四階微分控制方程的如何求解是得到樁身響應的關鍵。諸多學者相繼開展了以有限差分法、冪級數法、變分法、傳遞矩陣法等方法為基礎的組合受荷樁承載力計算方法研究，然而，有限差分法是一種純數值方法，對編程能力要求非常高，不適合工程設計人員使用；冪級數法和變分法的推導過程和解的形式非常繁瑣，極易出差且編程復雜，因而限制了其應用；現有的傳遞矩陣法其傳遞矩陣系數一般采用冪級數的方式表達且只能解決特定問題，因而限制了其應用范圍。

技術實現要素：

本發明的目的在于克服現有技術中的不足，提供一種組合受荷樁承載力傳遞矩陣通解方法，解決現有技術中組合受荷樁承載力計算方法步驟繁瑣、易出差、應用范圍受限的技術問題。

為解決上述技術問題，本發明所采用的技術方案是：組合受荷樁承載力傳遞矩陣通解方法，包括如下步驟：

步驟一：建立組合受荷樁通解受力分析模型并提出便于求通解時的樁土相互作用關系的統一表達式；

步驟二：根據傳遞矩陣的一維線性特征將土抗力系數、樁身軸力分布、樁身水平荷載分布進行離散化、均勻化以及常數化處理；

步驟三：采用Laplace正逆變換推導得出了樁身自由段、彈性段以及塑性段的傳遞矩陣系數的解析通解；

步驟四：在傳遞矩陣法原理基礎上代入樁頂樁端邊界條件，從而得出組合受荷樁承載力通解。

步驟一的具體步驟如下：

將線彈性、非線性彈性、線彈性-塑性以及非線性彈性-塑性樁土相互作用模型進行歸類，提出采用統一線彈性-塑性p-y曲線表達式模擬組合受荷樁樁土相互作用，如下式所述：

式中：p為土抗力；k為土抗力模量；y為樁身變形；p_u為極限土抗力。

步驟二的具體步驟如下：

根據土層分層以及樁身截面尺寸的變化，對地基土體重新進行n數量的分層，其中對第i層地基土體中的樁身再進行m_i數量的等分，則第j小段樁身平均軸向荷載為

其中：為第i層地基土中經過m_i等分后第j小段樁的樁身平均軸力荷載作用；

V_(i,j-1)，V_(i,j)分別為第i部分樁中第j小段樁的樁頂和樁端位置處的軸力荷載作用；

對于地面下樁土相互作用，根據其彈性、塑性狀態分為以下兩種：

①當樁土相互作用為彈性階段時，第i層地基土中經過m_i數量的等分后第j小段樁的樁側平均土抗力模量為：

其中：為第i層地基土中經過m_i數量的等分后第j小段樁的樁側平均土抗力模量；

k_(i,j-1)，k_(i,j)分別為第i部分樁中第j小段樁的樁頂和樁端位置處的土抗力模量；

②當樁土相互作用為塑性階段時，第i層地基土中樁經過m_i數量的等分后任意j小段樁側極限土抗力為

其中：為第i層地基土中樁任意j小段樁側平均極限土抗力值；

p_u(i,j-1)，p_u(i,j)分別為第i部分樁中第j小段樁的樁頂和樁端位置處的極限土抗力。

步驟三的具體步驟如下：

采用Laplace正逆變換對樁身自由段、彈性段以及塑性段的微分控制方程進行求解，得出以下傳遞矩陣系數解析解：

①對于考慮樁頂豎向荷載作用時的地面上自由段樁，其自由段第w小段樁的樁身傳遞矩陣系數表達式如下：

其中：l_a為自由段樁進行m_a數量等分后的每小段長度；為樁身自由段經過m_a等分之后任意w小段樁身平均軸向荷載作用；為樁身自由段經過m_a等分之后任意w小段樁側所受的平均水平荷載作用；ψ_a(w)＝α_a(w)l_a，EI_a為樁身抗彎剛度；

②對于不考慮樁頂豎向荷載作用時的地面上自由段樁，其自由段第w小段樁的樁身傳遞矩陣系數表達式如下：

③對于考慮樁頂豎向荷載作用時的地面下彈性段樁，其彈性階段的第i部分樁中第j小段樁的傳遞矩陣系數表達式如下：

式中：l_e(i,j)為彈性段進行m_i數量的等分后的第j小段樁的長度；ω_x(i,j)＝±(γ_i,j±ξ_i,ji)，x＝1、2、3和4，EI_i為第i層地基土位置處樁身抗彎剛度；

④對于不考慮樁頂豎向荷載作用時的地面下彈性段樁，其彈性階段的第i部分樁中第j小段樁的傳遞矩陣系數表達式如下：

式中：t_e(i,j)＝β_(i,j)l_e(i,j)；

⑤對于考慮樁頂豎向荷載作用時的地面下塑性段樁，其塑性階段的第i部分樁中第j小段樁的傳遞矩陣系數表達式如下：

式中：t_p(i,j)＝α_p(i,j)l_p(i,j)，l_p(i,j)為塑性段等分后的第j小段樁的長度，EI_i為第i層地基土位置處樁身抗彎剛度；

⑥對于不考慮樁頂豎向荷載作用時的地面下塑性段樁，其塑性階段的第i部分樁中第j小段樁的傳遞矩陣系數表達式如下：

根據傳遞矩陣原理，結合所推導的傳遞矩陣系數可得整個樁傳遞矩陣方程為：

式中：和S₀＝[y₀ θ₀ M₀ Q₀ 1]^T分別為整個樁的樁端和樁頂的位移、轉角、彎矩和剪力狀態量；

U_(i,j)為自由段矩陣傳遞系數或彈性段傳遞矩陣系數或塑性段傳遞矩陣系數，U為整個樁身的總傳遞矩陣系數，是從整個樁的樁端到樁頂的每小段樁的傳遞矩陣系數的連續乘積；

根據沿深度的樁土相互作用狀態以及是否存在自由段樁，總傳遞矩陣系數U求解過程如下：

①如果地面以上存在自由段樁時，則自由段樁身總傳遞矩陣系數U_a如下式：

則總傳遞矩陣系數U根據沿深度的樁土相互作用狀態按照下式進行計算：

②如果地面以上不存在自由段樁時，則總傳遞矩陣系數U根據沿深度的樁土相互作用狀態按照下式進行計算：

聯合樁頂、樁端的邊界條件和總傳遞矩陣系數U，即可解得樁頂變形、轉角、彎矩和剪力的狀態量S₀，進而按照下式計算任意位置處的樁身響應：

步驟四的具體步驟如下：

根據傳遞矩陣原理，代入樁頂與樁端的邊界條件進行建立樁身響應的傳遞矩陣表達式，并進行樁身變形與內力的求解，計算收斂關鍵步驟如下：

①根據計算模型確定相應的基本計算參數并進行離散化與常數化處理；對于樁土相互作用模型為非線性模型時需假定一個初始土抗力模量k；在計算初始階段需先假定樁土相互作用均為彈性狀態；

②根據上一次迭代的計算結果，如果存在非線性的樁土相互作用p-y曲線，則需要判斷經過r次迭代后割線剛度是否滿足公式的要求，如果滿足割線剛度迭代精度要求，則判斷經過s次迭代后整體精度是否滿足公式的要求；

其中，表示經過第r次迭代后的第i部分樁中第j小段樁的樁土相互作用p-y曲線割線剛度；ε表示迭代收斂標準推薦值；表示經過s次迭代后從地表往樁身方向發展的塑性區深度；

如果滿足要求則進行樁身響應最終狀態求解，如果不滿足上述2種迭代要求中的任意一種，則需要進行再次迭代直到兩種狀態的迭代精度均滿足要求。

自由段以及地面下樁身等分數量m_a和m_i確定原則為其等分后每小段的樁身長度要小于等于相應位置處樁身直徑的二十分之一。

對于樁土相互作用模型為非線性模型時，取該p-y曲線模型中y＝0.01mm所對應的割線剛度作為初始土抗力模量k。

迭代收斂標準推薦值為ε＝0.005。

與現有技術相比，本發明所達到的有益效果是：

本發明從組合受荷樁解的通用性角度出發，結合傳遞矩陣法的一維線性特征，提出離散化與均勻化的處理方法將每一微段單元的所有計算參數狀態轉換成常數量，并采用Laplace正逆變換求解變系數四階微分方程進而得出樁身自由段、彈性段以及塑性段的傳遞矩陣系數解析解表達式；本發明所闡述的計算方法能夠考慮任意的樁頂豎向荷載、水平荷載、彎矩荷載以及樁身自由段水平分布荷載的組合作用、樁身軸力荷載作用、樁土相互作用p-y曲線模型、樁身截面尺寸和長度以及任意多土層數量，同時傳遞矩陣系數解析解表達式非常簡潔，便于編程計算，具有非常好的適應性和通用性，能夠很好地解決巖土工程中遇到的各種工況下的組合受荷樁承載特性問題。

附圖說明

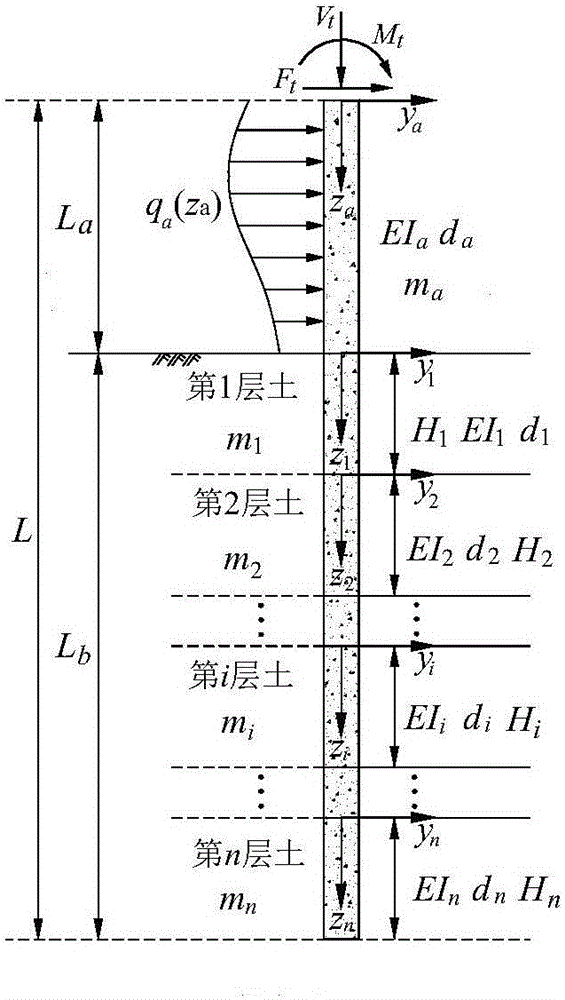
圖1為組合受荷樁受力分析通解模型；

圖2為樁土相互作用關系模型，其中圖2(a)為線彈性模型，圖2(b)為非線性彈性模型，圖2(c)為線彈性-塑性模型，圖2(d)為非線性彈性-塑性模型；

圖3為地面上自由段樁身微分單元受力模型；

圖4為地面下彈性段樁身微分單元受力模型；

圖5為地面下塑性段樁身微分單元受力模型；

圖6為沿樁身深度的樁土相互作用狀態示意圖，其中圖6(a)為塑性-彈性模型，圖6(b)為塑性-彈性-塑性-彈性模型，圖6(c)為塑性-彈性-塑性模型，圖6(d)為塑性-塑性模型；

圖7為基于Laplace正逆變換的組合受荷樁承載力傳遞矩陣通解算法計算流程圖；

圖8為線彈性樁土相互作用模型對比驗證；

圖9為非線彈性樁土相互作用模型對比驗證；

圖10為線彈性-塑性樁土相互作用模型對比驗證；

圖11為非線彈性-塑性樁土相互作用模型對比驗證，其中圖11(a)為樁身變形對比，圖11(b)為樁身彎矩對比；

圖12為組合受荷樁樁身彎矩對比驗證，其中圖12(a)為第一組樁，圖12(b)為第二組樁，圖12(c)為第三組樁，圖12(d)為第四組樁。

具體實施方式

下面結合附圖對本發明作進一步描述。以下實施例僅用于更加清楚地說明本發明的技術方案，而不能以此來限制本發明的保護范圍。

本發明從組合受荷樁解的通用性角度出發，結合傳遞矩陣法的一維線性特征，提出離散化與均勻化的處理方法將每一微段單元的所有計算參數狀態轉換成常數量，并采用Laplace正逆變換求解變系數四階微分方程進而推導得出樁身自由段、彈性段以及塑性段的傳遞矩陣系數解析解表達式，最后通過公知的傳遞矩陣原理進行求解任意位置處的樁身響應。具體計算步驟如下：

(1)建立組合受荷樁通用受力分析模型，如圖1所示，明確相應的各計算參數狀態。圖中L_a、L_b分別為樁位于地面上和地面下的長度；H_i、d_i、m_i、EI_i分別為地面下每層地基土中樁身的長度、直徑、等分數量以及抗彎剛度；d_a、m_a、EI_a分別為地面上樁身的直徑、等分數量以及抗彎剛度；自由段以及地面下樁身等分數量m_a和m_i確定原則為其等分后每小段的樁身長度要小于等于相應位置處樁身直徑的二十分之一。

(2)如圖2所示，將目前常用的線彈性、非線性彈性、線彈性-塑性以及非線性彈性-塑性樁土相互作用模型進行歸類，并提出模擬組合受荷樁樁土相互作用的統一p-y曲線表達式，

其中：p為土抗力；k為土抗力模量；y為樁身變形；p_u為極限土抗力。因此，對于彈性模型而言(圖2(a)和2(b))，采用p＝ky進行計算；當考慮塑性影響時(圖2(c)和2(d))，其彈性階段采用p＝ky計算，塑性階段采用p＝p_u計算。

(3)結合傳遞矩陣法的一維線性特征，提出離散化與均勻化的處理方法將每一微段單元的所有計算參數狀態轉換成常數量。因此對于地面上自由段樁而言(見圖3)，任意第w小段樁側所受的水平分布荷載按下式計算：

其中為任意w小段樁側所受的平均水平荷載作用，q_a(w-1)和q_a(w)為任意w小段樁頂和樁端位置處的水平荷載作用。

任意第w小段樁身所受平均軸力為：

其中為任意w小段樁身平均軸向荷載作用，V_a(w-1)和V_a(w)分別為任意w小段樁頂和樁端位置處的軸向荷載作用。

對于地面下彈性段樁而言(如圖4)，第i層地基土中經過m_i等分后第j小段樁的樁側平均土抗力模量為：

其中，為第i層地基土中經過m_i等分后第j小段樁的樁側平均土抗力模量；k_(i,j-1)，k_(i,j)分別為第i部分樁中第j小段樁的樁頂和樁端位置處的土抗力模量。

對于地面下塑性段樁而言(如圖5)，第i層地基土中樁的任意j小段樁側平均極限土抗力采用下式計算：

其中為第i層地基土中樁任意j小段樁側平均極限土抗力值；p_u(i,j-1)，p_u(i,j)分別為第i部分樁中第j小段樁的樁頂和樁端位置處的極限土抗力。

對于地面下樁而言(圖4和圖5)，對第i層地基土體中的樁身任意第j小段樁身平均軸向荷載采用下式計算：

其中，為第i層地基土中經過m_i等分后第j小段樁的樁身平均軸力荷載作用；V_(i,j-1)，V_(i,j)分別為第i部分樁中第j小段樁的樁頂和樁端位置處的軸力荷載作用。

則可得樁身響應變系數四階微分控制方程為：

地面上自由段：

地面下彈性段：

地面下塑性段：

(4)為采用Laplace正逆變換求解自由樁微分方程，將公式(7)采用矩陣方式表述：

式中，S_a(w)、A_a(w)和f_a(w)為矩陣變量，其中S_a(w)為自由段樁中第w小段樁的樁端狀態量，各矩陣變量如下所示：

S_a(w)＝[y_a(w) θ_a(w) M_a(w) Q_a(w)]^T (11)

式中：y_a(w)、z_a(w)、θ_a(w)、M_a(w)和Q_a(w)分別為地面上自由段樁經過等分m_a段后任意w小段樁的樁端位移、深度、轉角、彎矩和剪力。

為使用Laplace正逆變換，令：

L[S_a(w)(z_a(w))]＝F_a(w)(s_a(w))，L[f_a(w)(z_a(w))]＝g_a(w)(s_a(w)) (14)

其中，符號“L”表示Laplace正變換；F_a(w)和g_a(w)均表示Laplace方程，s_a(w)表示Laplace方程的變量。根據Laplace正變換原理，對公式(10)進行Laplace正變換得：

F_a(w)(z_a(w))＝(I×s_a(w)-A_a(w))^-1S_a(w-1)+(I×s_a(w)-A_a(w))^-1g_a(w)(s_a(w))

對公式(15)采用Laplace逆變換進行變換，可得：

S_a(w)＝L^-1[(I×s_a(w)-A_a(w))^-1]S_a(w-1)+L^-1[(I×s_a(w)-A_a(w))^-1g_a(w)(s_a(w))] (16)

式中：符號“L^-1”表示Laplace逆變換。S_a(w-1)為自由段樁中第w小段樁頂狀態量：

S_a(w-1)＝[y_a(w-1) θ_a(w-1) M_a(w-1) Q_a(w-1)]^T (17)

令：可得：

則公式(18)的Laplace逆變換為：

其中，ψ_a(w)＝α_a(w)l_a，l_a為自由段進行m_a數量等分后的每小段長度。

將公式(20)和(21)代入公式(16)，并根據傳遞矩陣法的原理可得：

S_a(w)＝U_a(w)S_a(w-1) (22)

式中，U_a(w)為自由段第w小段樁的傳遞矩陣系數，根據公式(20)和(21)可得：

當不考慮樁身軸力荷載作用時，對公式(23)求極限可得：

(5)為采用Laplace正逆變換求解彈性樁微分方程，將公式(8)采用矩陣方式表述：

式中，S_e(i,j)、A_e(i,j)和f_e(i,j)為矩陣變量，其中S_e(i,j)為位于彈性階段的第i部分樁中第j小段樁的樁端狀態量，各矩陣變量如下所示：

S_e(i,j)＝[y_e(i,j) θ_e(i,j) M_e(i,j) Q_e(i,j)]^T (26)

f_e(i,j)＝[0 0 0 0]^T (27)

對公式(25)進行Laplace逆變換可得：

S_e(i,j)＝L^-1[(I×s_e(i,j)-A_e(i,j))^-1]S_e(i,j-1)+L^-1[(I×s_e(i,j)-A_e(i,j))^-1g_e(i,j)(s_e(i,j))] (29)

式中，符號“L”表示Laplace正變換；F_e(i,j)和g_e(i,j)均表示Laplace方程，s_e(i,j)表示Laplace方程的變量。S_e(i,j-1)為位于彈性階段的第i部分樁中第j小段樁的樁頂狀態量，也是第(j-1)小段樁的樁端狀態量：

S_e(i,j-1)＝[y_e(i,j-1) θ_e(i,j-1) M_e(i,j-1) Q_e(i,j-1) 1]^T (30)

式中：y_e(i,j-1)、θ_e(i,j-1)、M_e(i,j-1)和Q_e(i,j-1)為第j小段樁的樁頂的位移、轉角、彎矩和剪力。

其中，

(I×s_e(i,j)-A_e(i,j))^-1g_e(i,j)(s_e(i,j))＝[0 0 0 0]^T (32)

在采用Laplace逆變換求解過程中，需要解得如下方程的根：

實際上大部分樁的樁身軸力則可得方程(33)根為：

ω_x(i,j)＝±(γ_i,j±ξ_i,ji)(x＝1,2,3,4) (34)

式中：符號“i”(正體)表示虛數，且令l_e(i,j)為彈性段進行m_i數量的等分后的第j小段樁的長度，則可得：

L^-1[(I×s_e(i,j)-A_e(i,j))^-1g_e(i,j)(s_e(i,j))]＝[0 0 0 0]^T (36)

將公式(35)和(36)代入公式(29)，并根據傳遞矩陣法的原理可得：

S_e(i,j)＝U_e(i,j)S_e(i,j-1) (37)

式中，U_e(i,j)為位于彈性階段的第i部分樁中第j小段樁的傳遞矩陣系數，根據公式(35)和(36)可得：

當不考慮樁身軸力荷載作用時，對公式(38)求極限可得：

式中：t_e(i,j)＝β_(i,j)l_e(i,j)。

(6)為采用Laplace正逆變換求解彈性樁微分方程，將公式(9)采用矩陣方式表述：

式中，S_p(i,j)、A_p(i,j)和f_p(i,j)為矩陣變量，其中S_p(i,j)為位于塑性階段的第i部分樁中第j小段樁的樁端狀態量，各矩陣變量如下所示：

S_p(i,j)＝[y_p(i,j) θ_p(i,j) M_p(i,j) Q_p(i,j)]^T (41)

公式(40)的Laplace逆變換為：

S_p(i,j)＝L^-1[(I×s_p(i,j)-A_p(i,j))^-1]S_p(i,j)+L^-1[(I×s_p(i,j)-A_p(i,j))^-1g_p(i,j)(s_p(i,j))] (44)

其中，符號“L”表示Laplace正變換；F_p(i,j)和g_p(i,j)均表示Laplace方程，s_p(i,j)表示Laplace方程的變量。

根據自由段、彈性段的基于Laplace正逆變換求解過程可得塑性段樁身傳遞關系為：

S_p(i,j)＝U_p(i,j)S_p(i,j-1) (45)

式中，U_p(i,j)為位于塑性階段的第i部分樁中第j小段樁的傳遞矩陣系數，為：

式中：t_p(i,j)＝α_p(i,j)l_p(i,j)，l_p(i,j)為塑性段等分后的第j小段樁的長度，EI_i為第i層地基土位置處樁身抗彎剛度。

當不考慮樁身軸力荷載作用時，對公式(46)求極限可得：

(7)根據傳遞矩陣原理，結合所推導的傳遞矩陣系數可得整個樁傳遞矩陣方程為：

式中：和S₀＝[y₀ θ₀ M₀ Q₀ 1]^T分別為整個樁的樁端和樁頂的位移、轉角、彎矩和剪力狀態量。U_(i,j)為自由段矩陣傳遞系數或彈性段傳遞矩陣系數或塑性段傳遞矩陣系數，根據具體的樁土相互作用狀態以及是否存在自由段樁進行決定。U為整個樁身的總傳遞矩陣系數，是從整個樁的樁端到樁頂的每小段樁的傳遞矩陣系數的連續乘積。根據沿深度的樁土相互作用狀態(如圖6)以及是否存在自由段樁，總傳遞矩陣系數U求解過程如下：

①如果地面以上存在自由段樁時，則自由段樁身總傳遞矩陣系數U_a如下式：

則總傳遞矩陣系數U根據沿深度的樁土相互作用狀態(見圖6)按照下式進行計算：

②如果地面以上不存在自由段樁時，則總傳遞矩陣系數U根據沿深度的樁土相互作用狀態(見圖6)按照下式進行計算：

聯合樁頂、樁端的邊界條件和總傳遞矩陣系數U，即可解得樁頂變形、轉角、彎矩和剪力如下所示：

樁頂自由-樁端自由：

式中：U_ij表示總傳遞矩陣系數U(5×5階)中的第i行第j列元素。

樁頂自由-樁端嵌固：

樁頂嵌固-樁端自由：

樁頂嵌固-樁端嵌固：

在樁頂狀態量S₀確定之后，進而按照下式計算任意位置處的樁身響應：

(8)根據傳遞矩陣原理，代入樁頂與樁端的邊界條件進行建立樁身響應的傳遞矩陣表達式，并編制相應的核心計算程序進行樁身變形與內力的求解，該程序計算收斂關鍵步驟如下(如圖7)：

①根據計算模型確定相應的基本計算參數并進行離散化與常數化處理，自由段以及地面下樁身等分數量m_a和m_i確定原則為其等分后每小段的樁身長度要小于等于相應位置處樁身直徑的二十分之一；對于樁土相互作用模型為非線性模型時，取該p-y曲線模型中y＝0.01mm所對應的割線剛度作為初始土抗力模量k；在計算初始階段需先假定樁土相互作用均為彈性狀態；

②根據上一次迭代的計算結果，如果存在非線性的樁土相互作用p-y曲線，則需要判斷經過r次迭代后割線剛度是否滿足公式的要求，如果滿足割線剛度迭代精度要求，則判斷經過s次迭代后整體精度是否滿足公式的要求；其中，表示經過第r次迭代后的第i部分樁中第j小段樁的樁土相互作用p-y曲線割線剛度；ε表示迭代收斂標準推薦值；表示經過s次迭代后從地表往樁身方向發展的塑性區深度；如果滿足要求則進行樁身響應最終狀態求解，如果不滿足上述2種迭代要求中的任意一種，則需要進行再次迭代直到兩種狀態的迭代精度均滿足要求。

以上所述，僅為本發明較佳的具體實施方式，但本發明的具體保護范圍并不局限于此，任何熟悉本技術領域的技術人員在本發明揭露的技術范圍內，可輕易得到變換和替換，都應涵蓋在本發明的保護范圍之內。因此，本發明的保護范圍應該以權利要求的保護范圍為準。

實施例

1、統一p-y曲線模型正確性驗證

鑒于不考慮豎向荷載作用時的水平受荷樁承載力計算研究文獻相比組合受荷樁要全面，因此，基于組合受荷樁不考慮軸向荷載作用的特例情況，對p-y曲線統一表達式正確性驗證。

①線彈性模型驗證

一根等直變截面樁嵌入砂層土和軟巖中。砂層厚度H₁＝7.925m，巖層厚度H₂＝12.192m。第一層砂土的土抗力模量為k₁＝1.04×10⁴z kN/m²(z從地面開始計算)；第二層軟巖的土抗力模量分別為k₂＝5.1386×10⁴+5.91×10³(z-7.925)kN/m²(根據經驗公式反算得出)和k₂＝4.9573×10⁴+7.419×10⁴(z-7.925)kN/m²(根據p-y曲線反算得出)。位于砂層中基樁直徑(d₁)和抗彎剛度(EI₁)分別為2.59m和9.9324×10⁷kN·m²；位于軟巖層中基樁直徑(d₂)和抗彎剛度(EI₂)分別為2.44m和7.8327×10⁷kN·m²。樁頂和樁端邊界均為自由邊界。國外某學者采用變分法提出了該問題的解析解。計算結果如圖8所示，可見本文所提出的基于Laplace正逆變換的傳遞矩陣解與國外學者基于變分法解析解的結果幾乎完全一致，對比結果證明了本發明方法推導的正確性，也驗證了本發明提出的p-y曲線統一表達式適用于線彈性樁土相互作用模型。

②非線彈性模型驗證

國外某學者開展了一根長45m、直徑1.83m的樁垂直嵌入8層黏性地基土中的水平承載特性的研究。該樁實際嵌入長度為43m(2m位于地面以上)，土體的彈性模量E_s＝500S_u，樁的彈性模量E_p＝30GPa，該學者采用有限差分法對該水平受荷進行計算，分析過程中樁土相互作用的p-y曲線采用雙曲線型p-y曲線，如下式所示：

式中，k_s＝0.943(z/z_ref)^0.016(d/d_ref)v_s^-0.078E_s^1.036E_p^-0.031，p_u取(3+γz/S_u+Jz/d)S_u或10S_u兩者中的最小值。樁頂水平的水平荷載F_t＝3000kN位于地表0.6m位置處，樁頂和樁端邊界條件均為自由邊界，土層參數詳見表1所示。

表1雙曲線模型基本計算參數

如圖9所示為本文基于p-y曲線統一表達式的傳遞矩陣半解析解與國外學者基于p-y雙曲線的有限差分解對比。從圖中可以看出本發明通解計算結果與國外學者的結果幾乎一致，對比結果證明了本發明方法推導的正確性，也驗證了本發明提出的p-y曲線統一表達式適用于非線性彈性樁土相互作用模型。

③線彈性-塑性模型驗證

國外某學者報道了一個在砂土中樁長12m、樁徑0.5m的水平受荷樁試驗，樁身抗彎EI_p＝1.02×10⁵kN·m²，砂土重度為10kN/m³，摩擦角為30度。該學者采用變分法求解了水平受荷樁樁身響應，計算過程中采用線彈性-塑性模型，該p-y模型的彈性段的土抗力模量k＝10000kN/m²，極限土抗力采用p_u＝3γzK_pd計算，其中樁頂施加水平荷載為F_t＝200kN，樁頂和樁端邊界條件均為自由邊界。則樁身變形對比如圖10所示，本發明方法解得的樁身變形與國外學者解幾乎吻合，對比結果證明了本發明方法推導的正確性，也驗證了本發明提出的p-y曲線統一表達式適用于線彈性-塑性樁土相互作用模型。

④非線彈性-塑性模型驗證

國外某學者報道了一個在雙層黏性地基土中樁長26.6m、樁徑1.02m的鋼管樁水平受荷試驗。鋼管樁壁厚為16mm，相應的樁身抗彎剛度為1.26×10⁶kN·m²。樁真實嵌入深度為25.6m(地面上長度為1m)。計算過程中，該學者采用經典的Matlock粘土p-y曲線模型模擬樁土相互作用，即API粘土p-y曲線模型，如下所示：

式中，y₅₀＝ρε₅₀d，ρ為相關系數，取2.5；ε₅₀為三軸儀試驗中最大主應力差一半時的應變值，計算參數如表2所示。

表2API粘土p-y曲線模型基本參數

樁身變形和彎矩對比如圖11所示，本發明方法所得樁身變形與彎矩結果與國外學者所得結果幾乎吻合，這證明了本文方法推導的正確性，也驗證了本文提出的p-y曲線統一表達式適用于線彈性-塑性樁土相互作用模型。

2、組合受荷樁承載力傳遞矩陣通解正確性驗證

國內某學者開展了組合荷載作用下單樁承載特性試驗研究。樁采用鋁合金材質的鋼管樁，樁自重γ＝27.1kN/m³，樁外徑為d＝0.016m，鋼管樁壁厚為t＝0.002m；樁總長度為H＝0.8m，樁身抗彎剛度為EI＝0.189kN·m²。試驗中，土體采用均質的砂性土，砂層表面以上存在一定長度的自由段樁，剩余部分樁全部嵌入均質的砂土中。由于是鋼管樁且壁厚較薄，因此假定樁身軸力為常數分布。采用如下的樁土相互作用表達方式：

其中，n_hs為水平土抗力系數，單位為kN/m³；z₀為等效深度，單位為m；b為深度的指數，單位為一；y_u(＝3d/80)為土體屈服位移，單位為m。

由于該學者開展試驗時所提供的參數不足以確定公式(54)中所有參數，因此根據圖12(a)所示的第一組試驗結果進行反算，得出n_hs＝5.84×103kN/m³、z₀＝0.3m和b＝0.8，其中y_u＝3d/80＝0.6×10^-3m。根據反算所得參數計算剩余三組試驗，所得樁身彎矩結果如圖12所示。通過圖12對比可以發現本發明所提出的組合受荷樁承載力傳遞矩陣通解結果與實測結果非常接近，且樁身彎矩最大值吻合非常好，這說明了本發明提成的一種基于Laplace正逆變換的組合受荷樁承載力傳遞矩陣通解算法的正確性以及計算的合理性。

以上所述僅是本發明的優選實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明技術原理的前提下，還可以做出若干改進和變形，這些改進和變形也應視為本發明的保護范圍。