一種基于改進的指數平滑灰色模型電力負荷預測方法與流程
本發明屬于短期電力負荷預測技術領域,尤其涉及一種基于改進的指數平滑灰色模型電力負荷預測方法。
背景技術:
電力是經濟發展的生產動力,是維持現代社會正常運作必不可少的條件,在國民經濟各個行業和人民生活中占有極其重要的位置。隨著經濟快速增長、居民收入水平的顯著提高,用戶用電需求快速增長,使得電力供需矛盾更加突出。此外,電力的特殊性在于無法大量儲存,這就要求電能的生產、輸送、分配和消費必須保持同步,也就是說,在正常運作情況下,電力企業的可用發電容量應該在任何時候都能滿足社會用電量的要求。在這種情況下,準確快速的電力負荷預測顯得尤為重要。精確預測電力負荷不僅有助于用戶選擇更恰當的用電方案,在提高設備利用率的同時,節約大量電費支出,從而降低生產成本、提高經濟效益,而且有利于優化電力系統資源,提高供電能力,最終達到節能減排的目的。具體體現在以下5點:(1)在電力系統經濟運行方面,可以為供電局制定購電計劃提供基礎,同時也可以保障發電廠制定合理的發電計劃,從而使得電力公司經濟可靠地運行;(2)在定制實時電價方面,合理的電價是電力市場的核心,而電力負荷預測可以為制定電價提供依據,在保證企業競爭力的同時合理提高盈利水平;(3)在用戶用電方面,精確的電力負荷預測有助于用戶合理安排用電情況,避免電能浪費,有效節約電費;(4)在轉運業務方面,精確的電力負荷預測可以使發電、輸電和用電之間更有效地協調在一起,提高發電效益;(5)在合理電量分配方面,精確的電力負荷預測有助于制定合理的電費方案,避免造成電量分配不合理等問題。總的來說,電力負荷預測是電力系統優化調度的基礎工具,可以十分有效地指導電網經濟、安全穩定地運行,有利于未來智能電網的發展。短期電力負荷預測通常包括三個關鍵環節:一是正確考慮影響因素,如經濟、時間、氣候、隨機干擾等;二是選擇正確的數學模型;三是正確的預測算法;其核心是負荷預測方法。電力負荷預測是一項重要的基礎性工作,電力負荷預測方法大致可以分為兩類,一類是統計類的經典預測方法,比如回歸分析法、時間序列法、灰色預測法等;另一類是人工智能類的新型預測方法,比如專家系統、人工神經網絡等。但不同的預測方法有著不同的適用場合,沒有一種方法是適用于一切電力系統的,這就需要根據不同的電力負荷情況選擇不同的預測模型。其中回歸分析法過分依賴于歷史數據,對樣本需求過大,無法反映實時與非線性的影響關系,且要求變量因素之間必須存在相關關系,預測誤差大;時間序列法對時間序列平穩性要求過高,一旦受到外界不確定因素的影響,將會失去預測效果;灰色預測法雖然所需樣本數據少,但模型本身存在缺陷,且要求數據符合指數變化趨勢,當數據存在波動時,預測誤差較大;專家系統法需要依靠大量的人工經驗來判斷外界因素對電力負荷的影響,定量分析比較困難;人工神經網絡法雖對分析處理任意復雜的非線性關系問題以及隨機的不確定性問題有著良好的解決能力,但對網絡層數和神經元個數的確定較為困難,且收斂速度慢,容易陷入局部收斂。
綜上所述,目前電力負荷預測方法存在受外界因素影響大、難以預測具有隨機波動性的數據、預測誤差大、可靠性低的問題。
技術實現要素:
本發明的目的在于提供一種基于改進的指數平滑灰色模型電力負荷預測方法,旨在解決目前電力負荷預測方法存在的難以預測具有隨機波動性的數據、預測誤差大、可靠性低的問題。
本發明是這樣實現的,一種基于改進的指數平滑灰色模型電力負荷預測方法,所述基于改進的指數平滑灰色模型電力負荷預測方法包括以下步驟:
步驟一,輸入實時更新的原始電力負荷數據,并采用一次指數平滑公式y0(k)=αx0(k)+(1-α)y0(k-1),對具有隨機波動性的原始電力負荷數據進行平滑處理,提高序列平滑性,弱化其隨機性,使其更接近指數發展趨勢;
步驟二,對平滑處理后的序列利用優化背景值的灰色預測模型進行預測,根據灰色預測公式
步驟三,將預測所得結果經過反指數平滑處理,還原為原始電力負荷數據與下一預測時刻的預測值;
步驟四,得到原始電力負荷數據與下一預測時刻的預測值后,利用原始電力負荷數據及其擬合值判斷預測結果是否達到擬合誤差要求,若達到擬合誤差要求,則輸出下一預測時刻的預測值,若沒有達到擬合誤差要求則繼續下一步;
步驟五,引入0.618優選算法,以mape為目標函數來尋求最優的平滑系數值;
步驟六,重新選取平滑系數子區間及試點平滑系數,并判斷試點平滑系數,若滿足|αi-αi'|<ε,則取最優平滑系數為αi*=(αi+αi')/2,并轉向步驟一,若不滿足,則取mape值小的平滑系數α值,并轉向步驟一。
進一步,所述基于改進的指數平滑灰色模型電力負荷預測方法包括:
第一步,實時動態更新原始電力負荷數據,并利用改進的指數平滑灰色模型進行預測,更新過程中保持原始電力負荷數據總數n=6不變,即選擇移動跨距為6,每遞推一個跨距就去掉一個“最老”的數據,加入一個“最新”的數據,使得每一次預測過程都對應一個特定的最優平滑系數,且在占用內存不變的情況下實現預測模型參數的實時修正;
所述移動跨距選擇進一步包括:
移動跨距的取值范圍一般為3~20,若想加大對原始數據的修勻力度,則n取大些,若希望加大對外界變化的反應力度,則n取小些,但取得過大會使得預測反應過于遲鈍,不能體現波動變化,取得過小會使得反應過于靈敏,不能體現整體發展趨勢,考慮到實際短期電力負荷數據總數,且綜合考慮各影響因素對電力負荷預測的影響,取移動跨距為6最為適宜,即每次都用最近的前6個時刻的電力負荷數據來預測下一個預測時刻的電力負荷數據;
第二步,選擇預測結果中與原始電力負荷數據相對應的擬合值,并計算原始數據與擬合數據之間的誤差;
第三步,判斷是否滿足擬合誤差要求,若滿足,則輸出下一預測時刻的預測值,若不滿足,則引入0.618優選算法尋求最優平滑系數。
進一步,所述改進的指數平滑灰色模型包括一次指數平滑處理、優化背景值的灰色預測模型與反指數平滑還原處理三個過程;
進一步,所述優化背景值的灰色預測模型,用于對平滑后的序列進行預測,具體按如下過程進行:
第一步,對得到的平滑序列y0進行一階累加,如公式y1(k)=y0(k)+y0(k+1),得到一階累加序列y1;
第二步,采用一次指數平滑處理過程中的平滑系數α,根據式(1)對灰色預測模型中的背景值z進行優化,并根據優化后的背景值式(2)求取數據矩陣y和b,最終得到灰參數a和u,計算公式分別如下所示:
z(k)=βy1(k-1)+(1-β)y1(k)(2)
y=[y0(2),y0(3),...,y0(n)]t(3)
第三步,根據灰色預測公式
進一步,所述第二步對灰色預測模型中背景值的優化是指,將灰色預測模型中背景值z的權值β取為與平滑系數α有關的值,可以避免β固定為0.5所帶來的誤差,有助于提高預測精度。
進一步,所述反指數平滑處理過程,用于實現對原始電力負荷數據與下一預測時刻數據的預測還原,將由灰色預測公式所得的預測序列yp0代入反指數平滑模型公式xp0(k)=(yp0(k)-(1-α)yp0(k-1))/α,最終得到原始電力負荷數據x0與下一預測時刻數據的預測序列xp0。
進一步,所述0.618優選算法具體按如下過程進行:
第一步,取ε=0.01,將平滑系數α∈(0,1)分為10個等距子區間:α1∈(0,0.1),α2∈(0.1,0.2),…,α10∈(0.9,1),并選取某一子區間αi∈(a0,b0)(i=1,2,...,10),進行下一步;
第二步,取第一個試點,令αi=0.618a0+0.382b0;
第三步,取第二個試點,令αi'=0.382a0+0.618b0;
第四步,判斷|αi-αi'|<ε是否成立,若成立,則取最優平滑系數αi*=(αi+αi')/2,并進行后續過程的處理,若不成立,進行第五步;
第五步,分別計算這兩個試點相對應的mape值f1(αi)和f2(αi'),并比較其大小,若f1(αi)<f2(αi'),則令a0不變,b0=αi',αi'=αi,f2(αi')=f1(αi),轉入第二步;若f1(αi)>f2(αi'),則令b0不變,a0=αi,αi=αi',f1(αi)=f2(αi'),轉入第三步。
進一步,所述0.618優選算法中第一步將平滑系數區間劃分為10個等距子區間,因在[0,1]整個區間上難以證明mape是單峰函數,等分區間就可能將mape的各極值點分布在不同的子區間中,使得mape在各子區間中是單峰函數,滿足0.618優選算法中目標函數為單峰函數的要求。
進一步,所述0.618優選算法中選擇mape作為目標函數,根據計算公式
本發明的另一目的在于提供一種所述基于改進的指數平滑灰色模型電力負荷預測方法的預測系統,所述預測系統包括:
輸入模塊,用于輸入實時電力負荷數據,更新原始數據序列,根據“近大遠小”的原則,去掉對預測影響最小的歷史數據,并輸入對預測影響最大的最新數據,確保預測過程能夠實時動態地涵蓋最新的電力負荷變化信息;
數據處理模塊,利用一次指數平滑方法弱化原始數據序列的隨機波動性,使得原始數據序列更加平滑地接近指數變化趨勢;
改造模塊,對灰色預測模型中的背景值進行改造優化,以避免由模型參數估計不準確所帶來的誤差;
預測模塊,對平滑處理后的數據序列采用灰色預測模型進行預測;
還原模塊,將由預測模塊所得結果還原為最終所需的原始電力負荷數據與下一預測時刻的預測值;
判斷模塊,用于判斷預測結果是否滿足擬合誤差要求,若達到擬合誤差要求,則輸出預測結果,沒有達到則轉入優選模塊;
優選模塊,用于重新選取平滑系數子區間及試點平滑系數,利用0.618優選算法,且以目標函數mape最小為尋優條件,選擇最優的平滑系數值;
計算模塊,用于分別計算兩個試點平滑系數相對應的mape值,并比較這兩個值,去掉較大的mape值及其對應的平滑系數值,保留較小的mape值及其對應的平滑系數值;
比較模塊,用于每一次重新選取平滑系數子區間及試點平滑系數后,判斷試點平滑系數是否滿足|αi-αi'|<ε,若滿足,則以最優平滑系數αi*=(αi+αi')/2進行預測,若不滿足,則計算mape值,并選擇最小mape值相對應的平滑系數,即為最終平滑系數α;
輸出模塊,用于在達到擬合誤差要求的條件下,輸出下一預測時刻的預測值。
本發明的另一目的在于提供一種包含所述基于改進的指數平滑灰色模型電力負荷預測方法的計算機信息處理系統。
本發明的另一目的在于提供一種包含所述基于改進的指數平滑灰色模型電力負荷預測方法的機器人。
本發明的優點及積極效果為:采用一次指數平滑模型處理原始電力負荷數據,不僅弱化了數據的隨機性,而且增強了數據的平滑性,使其更逼近指數變化趨勢,滿足灰色預測模型對輸入數據的要求,因灰色預測模型最終的預測方程為指數函數,故對特定的建模序列來說,其越接近指數規律,且序列變化越平滑,建模效果就越好,即有助于進一步提高預測精度;同時灰色預測模型中的背景值按式(1)進行優化改造,可以避免模型本身缺陷所帶來的誤差;在一次指數平滑過程中引入了0.618優選算法確定最優平滑系數,利用0.618優選算法的對稱原則和等比收縮原則,在每個子區間尋優的過程中都使得每次留下區間的長度大約是上次留下區間長度的0.5倍,即每次尋優都可以縮短近一半的搜索區間,使得每次收縮都較快,提高了求解效率,而且使用0.618優選算法進行尋優可以避免經驗估計法與試湊法的人為干預,增強求解過程的自動化程度;且采用mape作為0.618優選目標函數進行尋優,mape是目前應用最廣的預測精度評價指標,根據mape的計算公式
本發明提供的基于改進的指數平滑灰色模型電力負荷預測方法,擴大了灰色預測模型的適用范圍,縮短了搜索區間且預測可靠性高,預測精度高達97%以上,可以滿足短期電力負荷預測平均誤差在3%左右的要求,解決未來智能電網發展中短期電力負荷預測的問題。
附圖說明
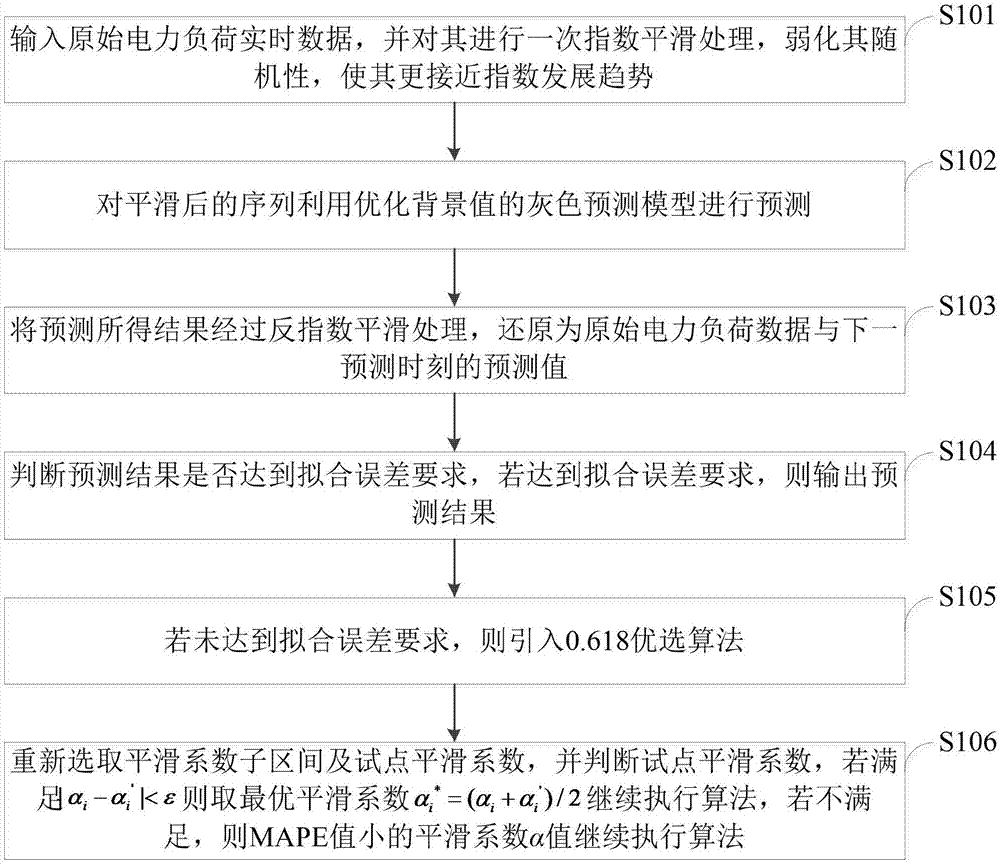
圖1是本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法流程圖。
圖2是本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法總體流程圖。
圖3是本發明實施例提供的改進的指數平滑灰色模型結構圖。
圖4是本發明實施例提供的0.618優選算法結構圖。
圖5是本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法預測值與實際值比較圖。
圖6是本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法預測誤差曲線圖。
圖7是本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法的預測系統總體結構圖。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合實施例,對本發明進行進一步詳細說明。應當理解,此處所描述的具體實施例僅僅用以解釋本發明,并不用于限定本發明。
下面結合附圖對本發明的應用原理作詳細的描述。
如圖1所示,本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法包括以下步驟:
s101:輸入實時更新的原始電力負荷數據,并對其進行一次指數平滑處理弱化其隨機性,使其更接近指數發展趨勢;
s102:對平滑處理后的序列利用優化背景值的灰色預測模型進行預測;
s103:將預測所得結果經過反指數平滑處理,還原為原始電力負荷數據與下一預測時刻的預測值;
s104:判斷預測結果是否達到擬合誤差要求,若達到擬合誤差要求,則輸出預測結果;
s105:若未達到擬合誤差要求,則引入0.618優選算法;
s106:重新選取平滑系數子區間及試點平滑系數,并判斷試點平滑系數,若滿足|αi-αi'|<ε,則取最優平滑系數為αi*=(αi+αi')/2,并繼續執行算法,若不滿足,則取mape值小的平滑系數α值,并繼續執行算法。
下面結合具體附圖對本發明的應用原理作進一步的描述。
如圖2所示,本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法包括:
首先,輸入原始電力負荷實時數據,并對其進行一次指數平滑處理,弱化其隨機性,使其更接近指數發展趨勢;其次,對平滑后的序列利用優化背景值的灰色預測模型進行預測;再次,將預測所得結果經過反指數平滑處理,還原為原始電力負荷數據與下一預測時刻的預測值;最后,判斷預測結果是否達到擬合誤差要求,若未達到,則引入0.618優選算法,重新選取平滑系數子區間及試點平滑系數,并判斷試點平滑系數,若滿足|αi-αi'|<ε,則取最優平滑系數αi*=(αi+αi')/2繼續執行算法,若不滿足,則取mape值小的平滑系數α值繼續執行算法;若達到擬合誤差要求,則輸出下一預測時刻的預測值。
本發明實施例提供的基于改進的指數平滑灰色模型電力負荷預測方法具體步驟如下:
第一步,實時動態更新原始電力負荷數據,并利用改進的指數平滑灰色模型進行預測;
第二步,選擇預測結果中與原始電力負荷數據相對應的擬合值,并計算原始數據與擬合數據之間的誤差;
第三步,判斷是否滿足擬合誤差要求,若滿足,則輸出下一預測時刻的預測值,若不滿足,則引入0.618優選算法尋求最優平滑系數。
所述預測方法第一步中為實現原始電力負荷數據的實時更新,且綜合考慮各影響因素對電力負荷預測的影響,在更新過程中保持原始電力負荷數據總數n=6不變,即選擇移動跨距為6,每遞推一個跨距就去掉一個“最老”的數據,加入一個“最新”的數據,使得每一次預測過程都對應一個特定的最優平滑系數,且在占用內存不變的情況下實現預測模型參數的實時修正。
所述預測方法采用改進的指數平滑灰色模型,包括一次指數平滑處理、優化背景值的灰色預測模型與反指數平滑還原處理三個過程,如圖3所示,所述一次指數平滑處理過程采用一次指數平滑公式y0(k)=αx0(k)+(1-α)y0(k-1),對具有隨機波動性的原始電力負荷數據進行平滑處理,提高序列平滑性,弱化其隨機性,使其更接近指數發展趨勢。所述優化背景值的灰色預測模型,用于對平滑后的序列進行預測,首先,對得到的平滑序列y0進行一階累加;然后根據公式(1)對灰色預測模型背景值進行優化改造,并根據公式(2)-(5)得到數據矩陣y和b及灰參數a和u;最后,根據灰色預測公式
所述一次指數平滑處理過程,就是采用0.618優選算法得到的最優平滑系數加權。
如圖4所示,所述0.618優選算法具體過程如下:
第一步,取ε=0.01,將平滑系數α∈(0,1)分為10個等距子區間:α1∈(0,0.1),α2∈(0.1,0.2),…,α10∈(0.9,1),并選取某一子區間αi∈(a0,b0)(i=1,2,...,10),進行下一步;
第二步,取第一個試點,令αi=0.618a0+0.382b0;
第三步,取第二個試點,令αi'=0.382a0+0.618b0;
第四步,判斷|αi-αi'|<ε是否成立,若成立,則取最優平滑系數αi*=(αi+αi')/2,并進行后續過程的處理,若不成立,進行第五步;
第五步,分別計算這兩個試點相對應的mape值f1(αi)和f2(αi'),并比較其大小,若f1(αi)<f2(αi'),則令a0不變,b0=αi',αi'=αi,f2(αi')=f1(αi),轉入第二步;若f1(αi)>f2(αi'),則令b0不變,a0=αi,αi=αi',f1(αi)=f2(αi'),轉入第三步。
用matlab編程實現所述基于改進的指數平滑灰色模型電力負荷預測算法,并將其應用于短期電力負荷預測中,用前6個數據進行建模,后12個數據進行預測驗證,得到預測結果如圖5所示。從圖中可以看出,電力負荷預測值與實際值變化趨勢很是接近,總體預測效果良好。預測誤差如圖6所示,預測最大mape誤差為5.19%,最小為0.22%,且經過實際計算,平均mape值為2.77%,滿足短期電力負荷預測平均誤差在3%左右的要求。
如圖7所示,所述基于改進的指數平滑灰色模型電力負荷預測方法的預測系統包括:輸入模塊、數據處理模塊、改造模塊、預測模塊、還原模塊、判斷模塊、優選模塊、計算模塊、比較模塊、輸出模塊。輸入模塊,用于輸入實時電力負荷數據,更新原始數據序列,確保預測過程能夠實時動態地涵蓋最新的電力負荷變化信息;數據處理模塊,利用一次指數平滑方法弱化原始數據序列的隨機波動性,使得原始數據序列更加平滑地接近指數變化趨勢;改造模塊,對灰色預測模型中的背景值進行改造優化,以避免由模型參數估計不準確所帶來的誤差;預測模塊,對平滑處理后的數據序列采用灰色預測模型進行預測;還原模塊,將由預測模塊所得結果還原為最終所需的原始電力負荷數據與下一預測時刻的預測值;判斷模塊,用于判斷預測結果是否滿足擬合誤差要求,若達到擬合誤差要求,則輸出預測結果,沒有達到則轉入優選模塊;優選模塊,用于重新選取平滑系數子區間及試點平滑系數,利用0.618優選算法,且以目標函數mape最小為尋優條件,選擇最優的平滑系數值;計算模塊,用于分別計算兩個試點平滑系數相對應的mape值;比較模塊,用于每一次重新選取平滑系數子區間及試點平滑系數后,判斷試點平滑系數是否滿足|αi-αi'|<ε,若滿足,則以最優平滑系數αi*=(αi+αi')/2進行預測,若不滿足,則計算mape值,并選擇最小mape值相對應的平滑系數,即為最終平滑系數α;輸出模塊,用于在達到擬合誤差要求的條件下,輸出下一預測時刻的預測值。
以上所述僅為本發明的較佳實施例而已,并不用以限制本發明,凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等,均應包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!