一種量測數據隨機缺失的線性變參數時滯系統的魯棒辨識方法與流程

本發明涉及工業系統建模以及工業系統模型參數辨識技術領域。

背景技術：

實際的工業系統，包括機械設備、發動機等，都屬于復雜的非線性系統，對這些系統的精確建模是控制和優化方法設計與實現的前提條件。而線性變參數模型能夠有效的對此類工業過程進行建模，其實際意義遠遠超過了傳統的建模方法。因此，對線性變參數模型的研究很有必要。

在利用線性變參數模型對復雜工業過程進行建模時，對已經建好的模型進行參數辨識需要考慮以下常見因素：存在系統時滯、系統的輸出數據隨機缺失、系統的輸出數據中含有異常值。這些因素都會很大程度上影響模型參數辨識的精度。

技術實現要素：

本發明的目的是為了解決現有技術存在系統時滯、系統的輸出數據隨機缺失、系統的輸出數據中含有異常值導致模型參數辨識精度較低的問題，而提出一種量測數據隨機缺失的線性變參數時滯系統的魯棒辨識方法。

一種量測數據隨機缺失的線性變參數時滯系統的魯棒辨識方法包括以下步驟：

步驟一：建立線性變參數(lpv)時滯模型；

步驟二：根據步驟一建立線性變參數(lpv)時滯模型，建立基于學生氏t-分布線性變參數(lpv)時滯魯棒概率模型；

步驟三：基于廣義期望最大化(generalizedexpectationmaximization，gem)算法，對步驟二建立的基于學生氏t-分布lpv時滯魯棒概率模型進行辨識，得到線性變參數時滯模型的參數θ^*,δ^*,d^*；其中θ^*為最優的模型參數多項式系數，δ^*為最優的尺度變量，為最優的自由度參數，d^*為最優的時間延遲。

本發明的有益效果為：

本發明方法在考慮系統時滯、輸出數據缺失、包含異常值的情況下，在gem算法的框架下，提出了一種lpv時滯系統的魯棒辨識方法，能夠有效的解決此類系統的模型參數辨識問題，對線性變參數系統辨識理論的完善及其工業實際應用起到了極大的促進作用。

將本發明方法lpvt-gem與經典方法lpv-riv(refinedinstrumentalvariable)對相同的仿真模型進行仿真，仿真結果的對比能夠很好的證明本發明方法的有效性。當輸出數據中包含不同比例的奇異值，信噪比的情況下，參數估計結果為：當真值為1時，本發明方法的均值為1.0014，標準差為0.0305，經典方法lpv-riv的均值為0.9462，標準差為0.0414；當真值為-0.5時，本發明方法的均值為-0.5039，標準差為0.0874，經典方法lpv-riv的均值為0.7054，標準差為0.4068；當真值為-0.1時，本發明方法的均值為-0.0861，標準差為0.1066，經典方法lpv-riv的均值為-1.5323，標準差為0.4517。當信噪比增加時，每個參數估計的標準差不斷減小，標準差越小，估計的效果越好；在信噪比一致的條件下，本發明方法lpvt-gem的參數估計效果要明顯好于作為對比的lpv-riv方法。

附圖說明

圖1為輸出數據缺失10％以及輸出異常值比例為10％的情況下，lpvt-gem方法中，q-函數的迭代過程圖。在圖中，q-函數的值不斷增加，在第25次迭代時，q-函數收斂；

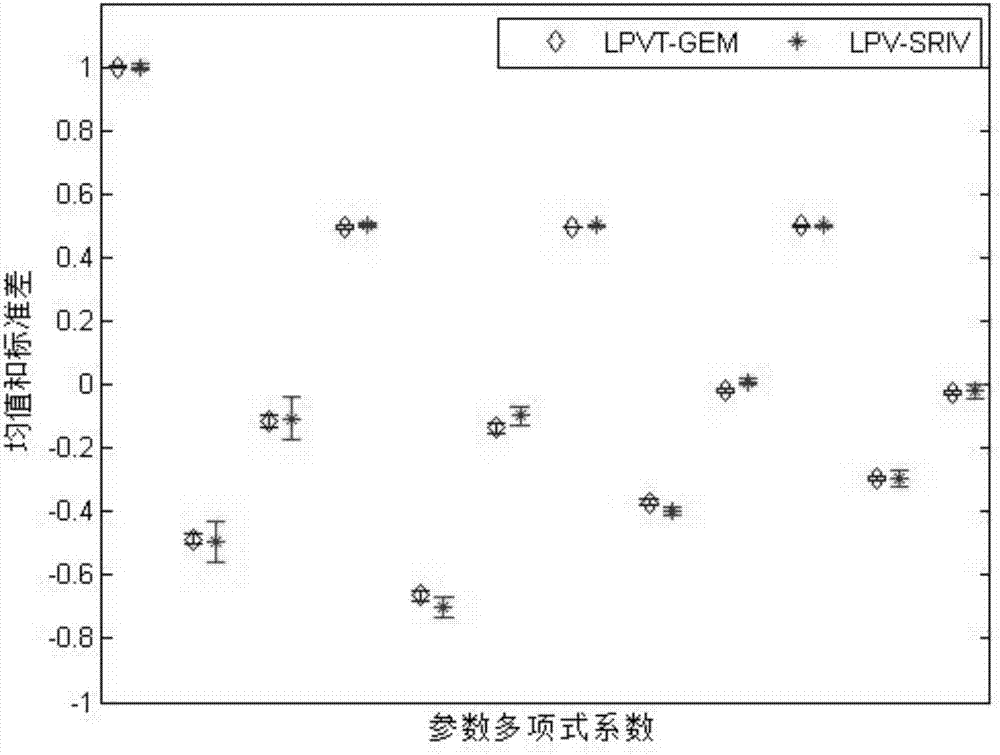
圖2為信噪比為snr＝20db以及輸出異常值比例為0％的情況下，lpvt-gem與lpv-riv方法的系統參數估計均值與標準差對比圖；

圖3為信噪比為snr＝10db以及輸出異常值比例為0％的情況下，lpvt-gem與lpv-riv方法的系統參數估計均值與標準差對比圖；

圖4為信噪比為snr＝5db以及輸出異常值比例為0％的情況下，lpvt-gem與lpv-riv方法的系統參數估計均值與標準差對比圖。

具體實施方式

具體實施方式一：一種量測數據隨機缺失的線性變參數時滯系統的魯棒辨識方法包括以下步驟：

步驟一：建立線性變參數(lpv)時滯模型；

步驟二：根據步驟一建立線性變參數(lpv)時滯模型，建立基于學生氏t-分布線性變參數(lpv)時滯魯棒概率模型；

步驟三：基于廣義期望最大化(generalizedexpectationmaximization，gem)算法，對步驟二建立的基于學生氏t-分布lpv時滯魯棒概率模型進行辨識，得到線性變參數時滯模型的參數θ^*,δ^*,d^*；其中θ^*為最優的模型參數多項式系數，δ^*為最優的尺度變量，為最優的自由度參數，d^*為最優的時間延遲。

θ^*：是最優的模型參數多項式系數，θ是模型參數多項式系數；δ^*為最優的尺度變量，δ為尺度變量；為最優的自由度參數，為自由度參數；d^*為最優的時間延遲，d為時間延遲；是模型參數。

具體實施方式二：本實施方式與具體實施方式一不同的是：所述步驟一中建立線性變參數時滯模型的具體過程為：

假設一個線性變參數(lpv)時滯系統用下面的線性變參數(lpv)輸出誤差(outputerror，oe)模型表示：

xk＝g(ωk,z^-1)uk-d

yk＝xk+εk

其中yk表示系統的輸出，xk為系統的無噪聲輸出，uk表示系統的輸入，ωk為可測量的調度變量，調度變量決定了系統的操作模式，d表示時間延遲，εk表示零均值的隨機噪聲；g(ωk,z^-1)表示輸入與輸出之間的傳遞函數，表示為：

其中的多項式a和b都是與調度變量ωk相關的；與調度變量ωk相關的也是就是，如果ωk的值改變，那么a和b的值也相應的改變；和b(ωk,z^-1)是兩個多項式，用來表示模型輸入與輸出之間的關系，為模型輸出前面的系數，用一個多項式來表示；b(ωk,z^-1)為模型輸入前面的系數，用一個多項式來表示。

寫成如下表達式：

其中na為模型輸出的階次；nb為模型輸入的階次；m和n為迭代變量，m的取值為：1，2，3……na，n的取值為：1，2，3……nb；ωk為可測量的調度變量，調度變量決定了系統的操作模式。z^-m為m階遞歸因子，物理含義為z^-mxk＝xk-m；z-n為n階遞歸因子，物理含義為z^-nxk＝xk-n；am(ωk)和bn(ωk)表示的是兩個函數；z^-1表示一個遞歸因子，它表示后退一個采樣時刻，比如：k時刻的模型無噪聲輸出為xk，k-1時刻的模型無噪聲輸出為xk-1，那么這兩個時刻的輸出之間的關系是z^-1xk＝xk-1；am(ωk)：是一個多項式函數，它表示k-m時刻，模型無噪聲輸出xk-m前面的系數；bn(ωk)：是一個多項式函數，它表示k-n-d時刻，模型輸入uk-n-d前面的系數。

在多項式a和b中，系數寫為ωk的亞純函數的線性組合：

其中表示為a(·)的伴隨矩陣，且等價于a(·)xk＝uk；{φi(ωk)},i＝0,…,nα和{χj(ωk)},j＝0,…,nβ是關于調度變量ωk的亞純函數，都有固定的表達式；na和nb表示lpv時滯系統的階數，nα和nβ表示系數函數的階數；這些階數假設為先驗已知的；亞純函數的意思就是：在a和b當分母的時候，不存在分母為0的情況。

由此可以看出，調度變量的改變會引起系統的動態特性變化，當調度變量為常值時，系統的動態特性也保持不變。根據上述描述，線性變參數(lpv)時滯系統的模型寫為：

a(ωk,z^-1)xk＝b(ωk,z^-1)uk-d

其中uk-d表示k-d時刻的模型輸入；

分別定義兩個維數為na(nα+1)+nb(nβ+1)的向量和θ如下：

其中θ是模型參數多項式系數(θ本身也是一個向量)；xk-1為k-1時刻的模型無噪聲輸出；xk-2為k-2時刻的模型無噪聲輸出；為k-na時刻的模型無噪聲輸出；uk-1-d為k-1-d時刻模型的輸入；uk-2-d為k-2-d時刻模型的輸入；為k-nb-d時刻模型的輸入；是[na×(nα+1)+nb×(nβ+1)]行，1列的向量，θ也是一個[na×(nα+1)+nb×(nβ+1)]行，1列的向量；

φ0(ωk)是構成as(ωk)的第一項亞純函數；

是構成as(ωk)的第nα項亞純函數，也是as(ωk)中最高階亞純函數，nα是已知的；

χ0(ωk)是構成bj(ωk)的第一項亞純函數；

是構成bj(ωk)的第nβ項亞純函數，也是bj(ωk)中最高階亞純函數，nβ是已知的；

θ由多項式函數以及多項式函數的全部系數組成，因此這個向量也被稱為模型參數多項式系數；：為多項式函數a1(ωk)的系數。

得到：

其中θ為自由度參數，表示向量的轉置。

其它步驟及參數與具體實施方式一相同。

具體實施方式三：本實施方式與具體實施方式一或二不同的是：所述步驟二中根據步驟一建立線性變參數時滯模型，建立基于學生氏t-分布線性變參數時滯魯棒概率模型的具體過程為：

一般來說，噪聲序列{εk}k＝1,…,n假設為零均值的高斯白噪聲，服從分布傳統的參數估計方法都是基于高斯分布模型。但是高斯分布模型對奇異值很敏感，用基于高斯分布模型的方法對包含奇異值的數據進行系統參數辨識，最終結果會偏離真值。

基于t-分布來建立lpv時滯系統的魯棒概率模型，步驟可分為：

步驟二一：將局部噪聲變化參數為δ/λk，由此得到：

其中δ為尺度變量，εk為噪聲序列，k＝1,….n；表示噪聲序列εk服從高斯分布，均值為0，方差為δ/λk；λk是權重參數：

其中表示gamma函數，表示自由度參數，根據輸出yk服從高斯分布，有：

步驟二二：yk的邊緣分布通過聯合邊緣分布對λk求積分得到：

通過上式不難看出，yk的邊緣分布實際上是一個t-分布，其中：表示自由度，δ表示尺度變量，其中γ(·)表示gamma函數，是服從gamma分布的概率密度。通過yk的邊緣分布表達式可以看出，t-分布可以看作是具有不同方差的無限個高斯分布的凸組合，每個高斯分布的組合權重具體由gamma分布來確定，這使得t-分布可以有效的應對各種奇異值對參數估計帶來的負面效應。表示一個后驗概率分布，物理意義是：在已知的情況下，變量λk的分布情況。在本發明中，是服從gamma分布的概率密度。

其它步驟及參數與具體實施方式一或二相同。

具體實施方式四：本實施方式與具體實施方式一至三之一不同的是：所述步驟三中廣義期望最大化算法的具體過程為：

<1>先作一個簡單符號解釋：

在整個辨識過程中，能夠直接獲取的數據集包括：輸入數據u1；n＝{uk}k＝1,…,n，輸出數據y1:n＝{yk}k＝1,…,n，調度變量ω1:n＝{ωk}k＝1,…,n。在本發明方法中，考慮了隨機缺失了部分數據，表示為未缺失的測量數據表示為并且，可用的測量輸出數據中還包含異常值。本發明中，需要估計的參數集可表示為：觀測數據集包括缺失數據集表示為：

<2>gem本質上是一種求解極大似然(maximumlikelihood，ml)估計的優化算法，通過兩個步驟：e-step(期望步驟)和m-step(最大化步驟)不斷迭代優化以達到最后的優化效果。在e-step中，先計算出完整數據集c＝{cobs,cmis}的對數似然函數logp(cmis,cobs|θ)，基于當前的參數估計θ^s和觀測數據集cobs，將對數似然函數對缺失數據集cmis求取期望，所得函數被稱為q-函數，其數學表達式為：

在m-step中，通過最大化q-函數，得到新的參數估計θ^s+1，再令θ^s＝θ^s+1，不斷循環迭代，直到最后全部被估計參數收斂。綜上所述，gem算法總結如下：

待估計的參數θ¹：在迭代開始之前，對需要辨識的模型參數θ賦予一個初始值，這個初始值θ＝θ¹；

步驟1)初始化：初始化待估計的參數θ¹，迭代次數s設為1；

步驟2)e-step：計算推導出q-函數：

其中logp(cmis,cobs|θ)為完整數據集c＝{cobs,cmis}的對數似然函數，θ^s為當前的模型參數(第s次迭代得到的線性變參數時滯模型的參數)，為觀測數據集，為系統輸出數據中沒有丟失的部分，u1；n為表示每一個時刻系統的輸入數據，ω1:n為表示每一個時刻系統的調度變量的值，為缺失數據集，為隨機缺失的數據，λ1:n為權重序列，是模型參數；表示logp(cmis,cobs|θ)的條件期望。

θ^s為上一次迭代得到的模型參數，也是這一次迭代的參數初始值，也就是當前的模型參數。

步驟3)m-step：通過最大化q-函數，得到新的參數估計θ^s+1，使得：

q(θ^s+1|θ^s)≥q(θ^s|θ^s)

再令：θ^s＝θ^s+1；

q(θ^s|θ^s)為上一次迭代中求得的q函數值；q(θ^s+1|θ^s)為本次迭代中，所希望得到的q函數值；

步驟4)令s＝s+1，返回到步驟2)，不斷重復執行e-step和m-step，直到最后待估參數收斂為止。收斂條件是：

其它步驟及參數與具體實施方式一至三之一相同。

具體實施方式五：本實施方式與具體實施方式一至四之一不同的是：所述步驟三中對步驟二建立的基于學生氏t-分布lpv時滯魯棒概率模型進行辨識，得到線性變參數時滯模型的參數θ^*,δ^*,d^*的具體過程為：

e-step:

(1)計算完整數據集c＝{cobs,cmis}的對數似然函數logp(cmis,cobs|θ)，利用概率鏈式法則，對數似然函數寫為：

此時，為了推導得到q-函數(q(θ|θ^s))，將上述對數似然函數分別對離散的時間延遲d、隨機缺失的數據權重序列λ1:n求取條件期望，可得：

其中τ為時間延遲，τ1表示時間延遲的下限值；τ2表示時間延遲的上限值；m1，m2，m3……mβ表示輸出數據隨機丟失的時刻；o1，o2，o3……oα表示輸出數據沒有丟失的時刻，輸出數據可用的時刻；n：表示系統的輸入輸出數據一共包含的采樣時刻數；

(2)為了計算q-函數，先計算d＝τ的后驗概率和上述公式中的所有積分項；d＝τ的后驗概率表示為：

其中δ^s為當前迭代中得到的尺度變量的值；為當前迭代中得到的自由度參數的值；uk-τ為k-τ時刻模型的輸入；g^s(ωk,z^-1)為當前迭代中，表示系統無噪聲輸出與輸入之間關系的多項式的值；pd,τ是上述p(d＝τ|cobs,θ^s)表達式的簡寫；

對于積分項，需要分情況討論：

當yk缺失時，λk的后驗分布表示為：

是gamma分布的數學表達式，其中的參數為當前迭代中得到的自由度參數的值；ψ(x)是一個函數，它是gamma函數γ(x)的一階導數，

λk以及logλk的期望為：

<λk>m＝∫p(λk|cobs,d＝τ,θ^s)λkdλk＝1

ψ(x)是gamma函數γ(x)的一階導數；

q-函數中的雙重積分表示為：

在雙重積分中，g^s(ωk,z^-1)表示傳遞函數在第s次迭代中，用該次迭代中得到的估計參數θ^s代替參數θ所得；

當yk屬于觀測數據時，λk的后驗分布表示為：

是一個gamma分布的數學表達式；

其中：

此時，λk以及logλk的期望為：

<λk>o是分配給每個觀測數據對應模型預測偏差的平方的權重；

(3)q-函數中，第二個積分項

中的積分運算可以寫為：

當yk屬于觀測數據集時，q-函數中第三個積分項

中的積分運算可以表示為：

當yk缺失時，第三個積分項可以寫為：

則q-函數表示為：

q1(θ,δ)表示關于變量θ,δ的函數，它是q(θ|θ^s)函數的一部分；表示關于變量的函數，它是q(θ|θ^s)函數的一部分；c1表示常數項，與所求的變量都沒有關系，所以在下面的m-step中，不需要考慮c1；

其中：

c1與任何變量都不相關，所以認為它是一個常量。

m-step：

步驟三一：為了計算尺度變量δ，將q1(θ,δ)對δ求導，并令導數等于零，得：

步驟三二：為了計算模型參數θ，將δ^s+1代入到函數q1(θ,δ)中，得到：

在準則函數q3(θ)中，<λk>o是分配給每個觀測數據對應模型預測偏差的平方的權重。如果yk是異常值時，<λk>o就非常趨近于零，因此可以很大程度上消除異常值對辨識算法帶來的負面影響。為了得到模型參數θ的估計表達式，利用阻尼牛頓方法優化準則函數q3(θ)，利用輔助模型準則構造輔助模型，并利用輔助模型的輸出來替代向量中的未知無噪聲輸出xk，得到模型結構參數θ的優化表達式如下：

其中μ表示阻尼牛頓常數，取值范圍在0到1之間；i為單位矩陣；

其中：

向量表示為：

基于當前的參數估計和輔助模型準則構造輔助模型，通過對下式中的輔助模型進行仿真求得

表示利用輔助模型求出來的無噪聲輸出估計值，表示利用無噪聲輸出估計值組成的遞歸向量；

步驟三三：為了估計自由度參數將函數對進行求導，并令求導結果等于零；得到：

解上述方程得參數的估計

步驟三四：獲得時間延遲d＝τ的估計值；假設τ均勻分布在整數區間[τ1,τ2]中，在每次迭代過程中，已經計算得到時間延遲d的后驗概率函數pd,τ，則d的估計值通過下式更新得到：

步驟三五：在m-step中，通過循環迭代步驟三一至步驟三四估計得到系統的模型參數，分別將最后的迭代結果記作：d^*；當算法收斂時對應得到的無噪聲估計就是最優的無噪聲輸出收斂條件是：

其它步驟及參數與具體實施方式一至四之一相同。

采用以下實施例驗證本發明的有益效果：

實施例一：

本實施例一種量測數據隨機缺失的線性變參數時滯系統的魯棒辨識方法具體是按照以下步驟實施的：

算法的輸入為算法的輸出包括：模型參數θ^*，尺度參數δ^*，自由度參數未知的時間延遲τ^*，無噪聲輸出估計

步驟一、分別構造觀測數據集：cobs和缺失數據集：cmis；

步驟二、初始化參數θ¹，并且設置s＝1；

步驟三、更新后驗概率分布以及期望：

利用e-step中給出的公式，在k＝1,…,n時，計算各個時刻λk的后驗分布以及期望<λk>m,<logλk>m,<λk>o,and<logλk>o；

τ在整數區間[τ1,τ2]中，對于整數區間[τ1,τ2]中的每一個值，計算τ的后驗概率分布；

步驟四、更新模型參數估計：

更新無噪聲輸出估計同時構造向量

更新模型參數估計θ，尺度參數δ，自由度參數時間延遲d；

步驟五、令s＝s+1，直到估計參數收斂。

<1>考慮下面的lpv時滯模型：

yk＝xk+εk

其中：

a(ωk,z^-1)＝1+a1(ωk)z^-1+a2(ωk)z^-2

b(ωk,z^-1)＝b1(ωk)z^-1+b2(ωk)z^-2

并且：

<2>設置仿真參數：

系統的輸入選取為均勻分布的隨機噪聲：調度變量選取為周期性函數：ωk＝0.5sin(0.35πk)+0.5，全部的數據長度設置為：n＝1500。為了驗證本發明方法對輸出數據中包含異常值和輸出數據隨機缺失等問題有效，假設輸出數據中包含10％異常值并且10％的輸出數據隨機缺失。

圖1展示了在每次迭代過程中，q-函數(q(θ^s+1|θ^s))值的變化情況，不難看出，q-函數的值一直在不斷增加，且在第25次迭代時，q-函數收斂。

<3>仿真驗證：

為了方便描述，將本發明方法簡記為：lpvt-gem。作為對比，我們利用經典方法lpv-riv(refinedinstrumentalvariable)對相同的仿真模型進行仿真，仿真結果的對比能夠很好的證明本發明方法的有效性。

lpv-riv方法是無法估計輸出時間延遲的，故而在lpv-riv方法的仿真中，我們假設τ＝2是已知的。

為了較好的驗證本發明方法，針對lpvt-gem和lpv-riv方法，在輸出數據中不包含奇異值、信噪比分別為snr＝20db、snr＝10db、snr＝5db的情況下，分別做了100次蒙特卡洛仿真，每組仿真將得到100個參數估計序列，求取每個參數的均值和標準差。具體的對比仿真結果見附圖2到附圖4。圖2為信噪比為snr＝20db以及輸出異常值比例為0％的情況下，lpvt-gem與lpv-riv方法的系統參數估計均值與標準差對比圖，菱形表示lpvt-gem方法參數估計的均值，*表示lpvt-riv方法參數估計的均值，菱形上的棒條表示lpvt-gem方法參數估計的標準差，*上的棒條表示lpvt-riv方法參數估計的標準差，棒條的長度越短，標準差越小，參數估計效果越好；圖3為信噪比為snr＝10db以及輸出異常值比例為0％的情況下，lpvt-gem與lpv-riv方法的系統參數估計均值與標準差對比圖，菱形表示lpvt-gem方法參數估計的均值，*表示lpvt-riv方法參數估計的均值，菱形上的棒條表示lpvt-gem方法參數估計的標準差，*上的棒條表示lpvt-riv方法參數估計的標準差，棒條的長度越短，標準差越小，參數估計效果越好；圖4為信噪比為snr＝5db以及輸出異常值比例為0％的情況下，lpvt-gem與lpv-riv方法的系統參數估計均值與標準差對比圖，菱形表示lpvt-gem方法參數估計的均值，*表示lpvt-riv方法參數估計的均值，菱形上的棒條表示lpvt-gem方法參數估計的標準差，*上的棒條表示lpvt-riv方法參數估計的標準差，棒條的長度越短，標準差越小，參數估計效果越好。

當輸出數據中包含不同比例的奇異值，信噪比的情況下，參數估計結果如下表所示：

表1異常值比例為10％、信噪比為snr＝5db時參數估計結果

仿真結果總結：

當信噪比增加時，每個參數估計的標準差不斷減小，標準差越小，估計的效果越好；

在信噪比一致的條件下，本發明方法lpvt-gem的參數估計效果要明顯好于作為對比的lpv-riv方法；

根據表1的仿真結果，可以看出在lpv-riv方法中，部分參數估計的結果是錯誤的，說明本發明方法對存在系統時滯、異常值、缺失輸出數據情況下有很強的魯棒性。

本發明還可有其它多種實施例，在不背離本發明精神及其實質的情況下，本領域技術人員當可根據本發明作出各種相應的改變和變形，但這些相應的改變和變形都應屬于本發明所附的權利要求的保護范圍。