一種延緩非定常狀態下轉子裂紋擴展的方法與流程

本發明屬于延緩轉子裂紋擴展
技術領域：
，特別涉及一種延緩非定常狀態下轉子裂紋擴展的方法。
背景技術：
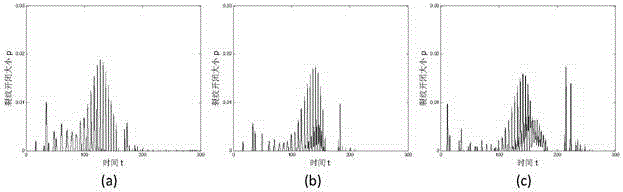
：由于轉子材料的缺陷或微裂紋的存在，以及轉子通常工作在多耦合場(高溫、高壓、高負荷)和周期性交變載荷共同作用的惡劣環境下，并伴隨著高速旋轉，因此轉子系統易誘發裂紋萌生與擴展，該問題所引起的故障對整個機械系統來說是極其危險的。國內外許多學者研究了裂紋轉子的振動特性，尋找轉子裂紋的在線診斷方法，通過監測旋轉機械的運轉狀況，在轉子發生災難性事故之前及早發現裂紋，監測裂紋的擴展，實現合理維修，防患于未然,在過去的許多年中，對轉子裂紋的在線診斷研究已經取得了一些成果。這些研究主要圍繞著裂紋模型、裂紋轉子動力學模型、裂紋轉子的動力學特性分析和裂紋診斷方法等進行了理論和實驗研究。現有的監測和檢測方法只能夠發現轉子裂紋的存在，防止災難性事故的發生，但是無法延緩轉子裂紋的擴展。此外，現有的延緩轉子裂紋擴展的方法基本上都是基于定常狀態下(加速度等于零)的，而沒有考慮非定常狀態下延緩轉子裂紋擴展的方法。技術實現要素：本發明的目的是提供一種延緩非定常狀態下轉子裂紋擴展的方法。為此，本發明技術方案如下：一種延緩非定常狀態下轉子裂紋擴展的方法，包括按順序進行的下列步驟：1)搭建用來測試延緩轉子裂紋的模型，首先將發動機轉子的轉軸通過軸承固定在兩個軸承支架上，將發動機轉子轉軸的一端通過聯軸器與電機的輸出軸相連；2)調整兩個軸承支架的垂直傾斜角度，通過軸承壓緊轉子的轉軸來增大轉子轉動過程中的非對稱非線性項值，通過減小轉子的轉軸在轉動過程中偏離軸承中心的位移來減小轉子轉動過程中的對稱非線性項值；3)給電機通電，使電機以固定的加速度大小帶動轉子增大轉速，當轉子的轉速達到工作轉速后，轉子做勻速運動；4)轉子勻速運行一段時間需要停止轉動時，控制電機以固定的加速度做勻減速運動，最終電機與轉子均停止轉動。所述的步驟1)中的電機的輸出軸與轉子的轉軸在同一高度。所述的轉子為jeffcott轉子。所述的轉子為帶有微裂紋的轉子。所述的步驟3)與步驟4)中加速度值均小于0.1。所述的步驟1)中的兩個軸承支架設置在關于轉子轉軸中心對稱的位置。與現有技術相比，該延緩非定常狀態下轉子裂紋擴展的方法可以有效地控制裂紋的開閉程度，從而延緩轉子裂紋的擴展。附圖說明圖1為轉子結構示意圖。圖2為轉子裂紋開閉程度大小示意圖。圖3為裂紋轉子坐標及參數示意圖。圖4(a)為加速度為0.01時的裂紋開閉程度大小仿真圖。圖4(b)為加速度為0.02時的裂紋開閉程度大小仿真圖。圖4(c)為加速度為0.05時的裂紋開閉程度大小仿真圖。圖5(a)為對稱非線性項值為0.1時的裂紋開閉程度大小仿真圖。圖5(b)為對稱非線性項值為0.2時的裂紋開閉程度大小仿真圖。圖5(c)為對稱非線性項值為0.25時的裂紋開閉程度大小仿真圖。圖6(a)為非對稱非線性項值為0.05時的裂紋開閉程度大小仿真圖。圖6(b)為非對稱非線性項值為0.15時的裂紋開閉程度大小仿真圖。圖6(c)為非對稱非線性項值為0.25時的裂紋開閉程度大小仿真圖。圖7(a)為加速度0.01，對稱非線性項值0.25，非對稱非線性項值0.05時的裂紋開閉程度大小仿真圖。圖7(b)為加速度0.02，對稱非線性項值0.2，非對稱非線性項值0.15時的裂紋開閉程度大小仿真圖。圖7(c)為加速度0.05，對稱非線性項值0.1，非對稱非線性項值0.25時的裂紋開閉程度大小仿真圖。具體實施方式下面結合附圖及具體實施例對本發明做進一步的說明，但下述實施例絕非對本發明有任何限制。如圖1所示，該一種延緩非定常狀態下轉子裂紋擴展的方法，包括按順序進行的下列步驟：1)搭建用來測試延緩轉子裂紋的模型，首先將發動機轉子的轉軸通過軸承固定在兩個軸承支架上，將發動機轉子轉軸的一端通過聯軸器與電機的輸出軸相連；2)調整兩個軸承支架的垂直傾斜角度，通過軸承壓緊轉子的轉軸來增大轉子轉動過程中的非對稱非線性項值，通過減小轉子的轉軸在轉動過程中偏離軸承中心的位移來減小轉子轉動過程中的對稱非線性項值；3)給電機通電，使電機以固定的加速度大小帶動轉子增大轉速，當轉子的轉速達到工作轉速后，轉子做勻速運動；4)轉子勻速運行一段時間需要停止轉動時，控制電機以固定的加速度做勻減速運動，最終電機與轉子均停止轉動。所述的步驟1)中的電機的輸出軸與轉子的轉軸在同一高度。所述的轉子為jeffcott轉子。所述的轉子為帶有微裂紋的轉子。所述的步驟3)與步驟4)中加速度值均小于0.1。所述的步驟1)中的兩個軸承支架設置在關于轉子轉軸中心對稱的位置。本發明提供的延緩非定常狀態下轉子裂紋擴展的方法的實施過程如下：帶有裂紋的轉子一端由單列深溝球軸承支承，另一端由雙列自動調心球軸承支承時，轉子受單列深溝球軸承結構限制恢復力會出現不同類型的非線性因素，首先，得到轉子極坐標下對應的勢能V；V=12(x2+y2)+ϵ30x3+ϵ21x2y+ϵ12xy2+ϵ03y3+β40x4+β31x3y+β22x2y2+β13xy3+β04y4---(1)]]>對公式(1)在x和y方向上做偏導可以求得支承處x方向與y方向的非線性恢復力Nx和Ny分別為：Nx=ϵc(1)(3x2+y2)+2ϵs(1)xy+4β(0)x(x2+y2)---(2)]]>Ny=ϵs(1)(x2+3y2)+2ϵc(1)xy+4β(0)y(x2+y2)---(3)]]>其中β(0)為對稱非線性項，ε(1)c和ε(1)s為非對稱非線性項；其次，根據圖2將轉子裂紋的開閉程度表示出來，從圖2中的幾何關系可知：tanγ＝R/0.5L(4)tanη=0.5τ/a2-(0.5τ)2---(5)]]>又因為tanγ＝tanη(6)其中，a為裂紋深度，L為轉子長度，R為轉子的振動幅值，τ為轉子在圖2位置時的裂紋開閉程度；由公式(4)、公式(5)、公式(6)可得：轉子在圖2位置時的裂紋開閉程度τ的表達式為：τ=4aR/L2+4R2---(7)]]>當圖3中的轉渦差角為零時，此時轉子正處于圖2中轉子所處的位置，即裂紋處于完全打開的狀態，轉渦差角為π/2時，轉子裂紋處于半開半閉狀態，由于此時裂紋根部受到的由裂紋開閉引起的撕扯已經很小，認為裂紋的開閉程度為零，值由0到π/2的過程用余弦函數對轉子裂紋開閉程度做近似處理，得到該過程中的裂紋開閉程度當繼續增加，轉子裂紋經歷由半開半閉到全閉的過程，此時p＝0；轉子x，y方向運動方程的一般表達式為：{mx··+ξx·+kx+Nx=mreω2cos(ω0t+12ct2+φ0)+mrecsin(ω0t+12ct2+φ0)+mgmy··+ζy·+ky+Ny=mreω2sin(ω0t+12ct2+φ0)+mreccos(ω0t+12ct2+φ0)---(8)]]>其中m為質量，ξ為阻尼，k為剛度，c為加速度；圖3中轉子在η方向的剛度模型為：圖3中轉子在方向的剛度模型為：圖3中轉子在η與耦合方向的剛度模型為：通過轉子運動方程與轉子剛度模型的結合將轉子啟停階段加速度c與轉子裂紋開閉程度p建立聯系，并采用MATLAB仿真軟件對該方法進行驗證：實施例一：當僅在轉子的啟停過程中對轉子的啟停加速度大小進行調整時，采用MATLAB軟件繪制轉子在啟停過程中加速度大小與轉子裂紋開閉程度大小的仿真圖，如圖4所示，通過觀察可知，隨著轉子啟停加速度大小的增加，裂紋開閉程度顯著減小，并且縮短了裂紋開閉的作用時間，大大減小了裂紋的開閉次數；因此，當轉子已經存在裂紋時，在轉子的起始和停車階段可以通過適當增大加速度值的方式，減小裂紋的開閉程度和開閉次數，從而實現對轉子裂紋擴展的延緩。實施例二：當僅對轉子的對稱非線性項值進行調整時，采用MATLAB軟件繪制轉子的對稱非線性項值與轉子裂紋開閉程度大小的仿真圖，如圖5所示，通過觀察可知，當值由0.1增加到0.2時對應相同時刻的裂紋開閉程度前部有所減小，后部反而增加，并且裂紋開閉次數顯著增加，當值由0.2增加到0.25時對應相同時刻的裂紋開閉程度前部有增有減，后部顯著增加，并且裂紋開閉的次數顯著增加，即當對稱非線性項值較大時不利于轉子裂紋擴展的延緩，因此可以通過調整對稱非線性項值的減小，實現對轉子裂紋擴展的延緩。實施例三：當僅對轉子的非對稱非線性項值進行調整時，采用MATLAB軟件繪制轉子的非對稱非線性項值與轉子裂紋開閉程度大小的仿真圖，如圖6所示，隨著非對稱非線性項值的增加對應相同時刻的裂紋開閉程度有減小，開閉次數也同樣減少，因此可以通過調整轉子支撐非對稱非線性項值的增大，實現對轉子裂紋擴展的延緩控制。實施例四：當同時對轉子啟停時的加速度大小、轉子對稱性非線性項值、轉子非對稱性非線性項值進行調整時，采用MATLAB軟件繪制轉子裂紋開閉程度仿真圖，如圖7所示，隨著轉子啟停過程中加速度值的增加，對稱非線性項值的減小和非對稱非線性項值的增加，轉子裂紋開閉程度大小顯著減小且開閉次數也顯著減小。當前第1頁1 2 3