借助于衍射元件的用于超短激光脈沖的空間重組的系統的制作方法

本發明的領域為大量超短脈沖激光源(也即脈沖寬度小于1皮秒)的相干重組的領域。本發明的架構涉及這些激光脈沖的空間重組技術，這些激光脈沖被假定為在其他方面是完全同步的。

背景技術：

超短脈沖激光源的相干重組尤其應用于高能激光源的實現。

根據選擇在遠場中并置光束或者選擇在近場中(也即在系統的出射光瞳的水平)疊加光束，用于對相干光束進行空間重組的方法分為兩種類型。

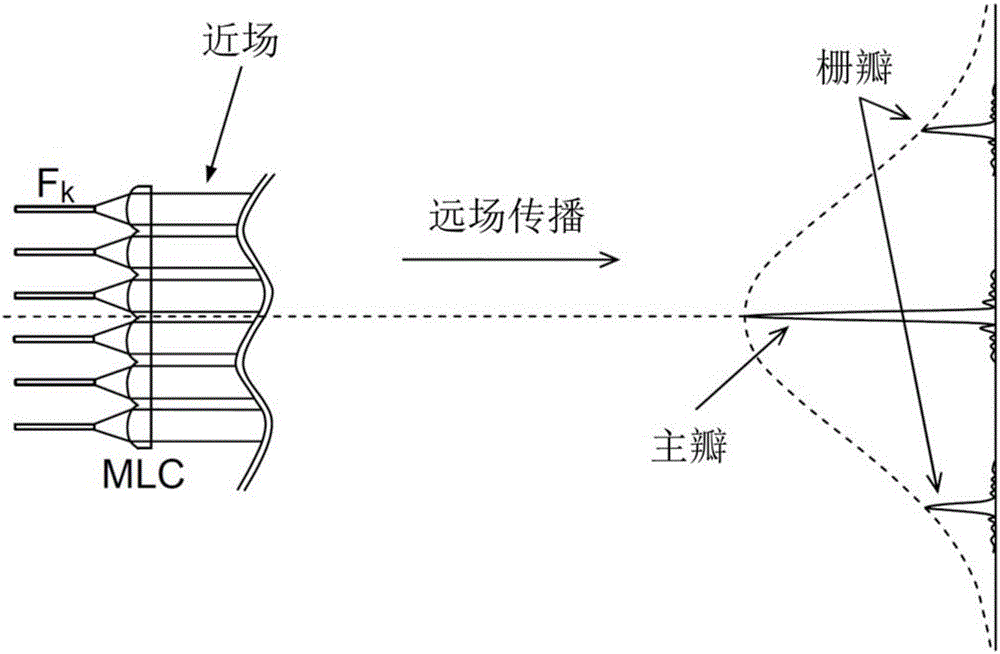
圖1a中顯示了用于通過并置來重組的系統。在這種情況下，從激光源F_k(k從0變化至N)產生的待重組的光束通過校準透鏡陣列MLC而在近場中為平行且校準的，并且以盡可能緊湊的方式而彼此并排地設置。然后通過自由傳播直到遠場而執行光束的疊加。這種系統不牽涉任何色散硬件部件，并且因此等同地應用于小于1皮秒的脈沖寬度。然而，這種系統的主要缺點在于其相對較低的效率，尤其是柵瓣中的能量損失具有相當大的份額。

對于近場疊加系統而言，其例如能夠通過利用電磁場的偏振來重組光束：從激光源F_k產生并且通過校準透鏡CL_k而校準的光束借助于分別關聯于半波片HWP_k的偏振分光立方體PBS_k而在近場中疊加，如圖1b中的示例所示。根據該系統，對于N個光束的重組效率由下式給出：

其中，η是每對(偏振分光立方體/半波片)的透射系數。該架構的優點在于，對于較少數量的待重組的光束而言，其實現相對容易：通常最大約10個。一方面，對于大量的光束，該系統的實現變得非常復雜，而另一方面，重組效率隨光源的數量而迅速下降(在η＝99％的情況下，對于1000個重組光束，效率下降至10％)。

無論是涉及通過校準和平行光束的自由傳播而在遠場重組，還是涉及通過利用分光片或偏振分光立方體的近場光束的疊加，這些系統都不適用于大量脈沖(通常>100或實際上>1000)的重組，即由于效率的問題(遠場設備的柵瓣)或近場系統的實現的問題。

用于通過疊加來重組的另一種技術利用衍射光學元件來組合光束。根據圖1c所示的該技術，傅里葉變換設置中的透鏡23能夠校準待重組的光束(所述光束從激光源F_k產生)，并且將光束導向位于透鏡23的焦平面的衍射光學元件或DOE 1。在透鏡23的物平面A中的光源點的空間分布(周期為P_A的周期性分布)變換為入射在光學元件DOE 1上的角度的分布。光學元件1通常是周期性相位光柵(例如，達曼光柵類型的周期性相位光柵)，其確保了所有入射光束在0級的相長干涉以及在所有其他級的相消；該光柵的周期Λ和入射角度θ_2k通過用于衍射光柵的已知公式而相關聯：

該架構的優點尤其在于高效率(在連續方式下展現出超過90％的效率)，并且由于這種集合定位、可能的二維布置以及單一透鏡的使用，該架構是非常適于大量光束(通常>100)的架構。另一方面，這種技術不能原樣應用于超短脈沖方式中。

待解決的技術問題在于，盡可能高效率地通過相干過程而將激光脈沖的每個的能量轉換成單個脈沖，同時相對于基本脈沖而盡可能少地降低最終脈沖的光束品質，并且同時可兼容于大量的加和的脈沖以及亞皮秒的脈沖持續時間。

技術實現要素：

提出的方案基于利用衍射光學元件DOE來組合光束，從而通過疊加來進行重組。根據本發明，光學衍射組件放置在該衍射光學元件的上游，從而能夠經由適當的成像系統來優化超短脈沖方式的組合效率。

更確切而言，本發明的主題為一種用于脈沖激光束的空間重組的系統，所述脈沖激光束具有以λ₀為中心的相同波長，并從N個同步的光源k產生，其中k從1變化至N，N為大于1的整數，所述系統具有光軸，并且包括：

-具有焦長f₂的傅里葉透鏡，其具有預定的物平面和預定的像平面，激光束在物平面(平面A)中展現出在λ₀具有間隔P_A的周期性空間結構，

-重組衍射光學元件，其具有周期性相位輪廓，N個光束旨在通過所述傅里葉透鏡根據入射角度θ_2k而被引導至所述重組衍射光學元件上，這些入射角度從一個光束至下一光束而不同，且根據重組衍射光學元件的周期而確定，

其主要特點在于，所述光源能夠發射持續時間小于10^-12s的脈沖，并且在于，所述系統包括：

-N個補償衍射光學元件(DOE)，其具有周期性光柵、入射角度θ_1k和光柵間隔Λ_1k，其中，每個光源具有一個補償衍射光學元件，所述入射角度θ_1k從一個光束至下一光束而不同，以及所述光柵間隔Λ_1k在相鄰補償衍射光學元件之間不同，

-透鏡陣列，每個光源具有一個透鏡，所述透鏡陣列具有預定的物平面和預定的像平面，與傅里葉透鏡形成具有預定放大率γ的雙-傅里葉變換設置，所述雙-傅里葉變換設置能夠將每個補償衍射光學元件成像在重組衍射光學元件上，補償DOE位于透鏡陣列的物平面，重組DOE位于傅里葉透鏡的像平面，透鏡陣列的像平面與傅里葉透鏡的物平面重合，

并且在于，對于每個補償DOE，在補償DOE上的光束的入射角度θ_1k、補償DOE在光軸上的傾斜角度Θ_k以及補償DOE的光柵的間隔Λ_1k，基于重組衍射光學元件的間隔P_A、k、λ₀、放大率γ、焦長f₂以及周期而確定。

根據本發明的一個實施方案，補償DOE的傾斜角度Θ_k為零，所述DOE位于同一平面。

所述光源可以根據一維或二維空間結構而設置。

優選地，補償DOE光柵為閃耀光柵。

根據本發明的特性，從激光源產生的光束具有同一出射面，并且該系統包括另一傅里葉透鏡，所述另一傅里葉透鏡具有物平面，所述激光源的出射面以及激光源的像平面位于所述另一傅里葉透鏡的物平面。該透鏡的像平面相對于補償衍射光學元件的組件所位于的平面的位置，以及在該透鏡的物平面中的光源的分隔，根據傅里葉透鏡的焦長、周期P_A和角度θ_1k而確定。

附圖說明

通過閱讀下述通過非限制性示例并且參考附圖而給出的具體描述，本發明的其它特征和優點將變得明顯，在附圖中：

已描述的圖1示意性地表示了用于在近場(圖1a)、遠場(圖1b)以及通過衍射元件(圖1c)而進行相干光束的空間重組的系統；

圖2示意性地示出了由用于通過衍射元件進行相干光束的空間重組的系統所產生的問題：色散(圖2a)、空間重疊缺陷(圖2b)以及重疊系數根據光瞳尺寸的示例性曲線(圖2c)；

圖3示意性地示出了根據本發明的由用于通過衍射元件進行相干光束的空間重組的系統所滿足的條件；

圖4示意性地表示了根據本發明的用于通過衍射元件進行相干光束的空間重組的示例性系統；

圖5示意性地表示了對于單個光源，根據本發明的用于光束的空間重組的系統的色散補償原理和空間重疊優化原理(圖5a)，在補償DOE水平示出在穿過補償DOE時的脈沖的空間分布的傾斜的更具體的視圖(圖5b)，以及示出補償DOE根據入射角度和光柵的傾斜的光柵矢量的幾何構造和入射波矢量的幾何構造的相應幾何構造(圖5c)；

圖6示意性地示出了對于兩個不同波長，在補償DOE(圖6a)和組合DOE(圖6b)上的衍射角度的圖解確定；

圖7示出了用于對在組合DOE上的脈沖的重疊進行優化以及對色散進行補償的入射角度和補償光柵的傾斜的示例性計算；

圖8顯示了在有利于顏色補償時(圖8b)或者有利于重疊缺陷的補償時(圖8a)，利用設置在同一平面中的補償DOE，根據本發明的用于光束的空間重組的系統的兩個示例性實施方案。

從一個附圖至下一個附圖，相同的元件由相同的附圖標記來標記。

本說明參考附圖所描述附圖的方位而給出。在該系統可以根據其他方位而設置的情況下，方向的術語僅以說明的方式指示，而并非是限制性的。

具體實施方式

當系統旨在對具有典型地小于1皮秒的脈沖寬度的脈沖激光源進行重組時，在對如圖2所示的具有DOE的重組系統的設置中存在兩個難點：

-第一個難點相關于脈沖的光譜寬度(通常大約為，對于Δt～100.10^-15s，Δλ＝10nm)。衍射元件1針對給定的工作波長而設定和制造。然而，大約10nm的光譜寬度不會嚴重影響DOE的重組的效率(通常，對于10nm的光譜寬度，效率損失為百分之幾)。另一方面，DOE的角分散δθ₀更成問題(脈沖的光譜中的藍色成分將與紅色成分以不同的角度離開DOE，如圖2a所示)。

該效應一方面由于增大了重組光束的發散而對重組光束的空間品質不利，并且另一方面使光束的空間色散變差，并暫時地加寬了脈沖。

-第二難點相關于在DOE上具有不同入射角度的短脈沖的空間重疊。該效應示出于圖2b中，并且相關于脈沖的受限空間范圍：在光的傳播方向的橫斷面限制于2ω(在1/e²)，而在光的傳播方向限制于c.Δt(c為光速，Δt為脈沖的持續時間)。對于在傳播方向之間的零角度存在脈沖的完全重疊，而隨該角度增大，重疊減小。在圖1c示出的應用中，對于等于1的數值孔徑，傳播方向之間的角度取決于所使用的傅里葉透鏡23的焦長，其最小值等于平面A中的整個光瞳的尺寸，即通道(一維，或者根據激光源的設置的圖案的直徑)的數量與在平面A中的兩個連續光源之間的間隔的乘積。圖2c給出了對于傅里葉透鏡的焦長的最優值，根據在平面A中的光瞳的尺寸所計算的脈沖(具有300.10^-15s的持續時間)之間的重疊系數。該計算清楚地示出對于通常大于10的通道數量(在一維)，以短脈沖的方式(<10^-12s)，不可能高效地利用如圖1c所示的架構。

最終，利用光學衍射元件DOE的重組系統(其確保了所有脈沖沿單個傳播方向的相長干涉，以及沿其他方向的相消)，可以是用于重組大量脈沖的很好的候選者，但是其在超短脈沖方式中受到兩個主要問題的影響：

-相關于脈沖的光譜寬度的問題，以及

-由于光束的入射角度的分布而導致的脈沖在DOE水平的空間重疊的缺陷。

根據本發明的系統包括補償結構，其技術效果為實現了圖3所示的條件，也即：

-一方面，脈沖的光譜的紅色成分和藍色成分必須以不同的入射角度到達組合DOE 1，所述不同的入射角度計算為使得，無論波長如何，離開這個組合DOE的波矢量全部沿著該附圖的z軸；

-另一方面，無論脈沖在組合DOE上的入射角度如何，在設定時刻的能量的空間分布必須平行于組合DOE 1，即平行于附圖的yOx平面，這是為了優化脈沖在組合DOE上的空間重疊。

結合圖4、圖5a、圖5b和圖5c來描述這種補償結構2。

通過成像設備將第一衍射補償組件21成像在組合DOE 1上。該成像設備包括：

-通過間隔P_A隔開的具有焦長f₁的M個透鏡(每個光束一個透鏡)的陣列22，P_A為在平面A中在λ₀的光束的空間周期，以及

-具有焦長f₂的傅里葉透鏡23，其具有至少等于N×f₁的孔徑，N為激光源的數量(沿著圖5a所示的維度)。

透鏡陣列22與傅里葉透鏡23形成具有預定放大率γ的雙FT設置，其能夠將衍射光學補償組件21成像在重組衍射光學元件1上。衍射光學補償組件21位于透鏡陣列22的物平面，重組DOE 1位于傅里葉透鏡23的像平面，透鏡陣列22的像平面與傅里葉透鏡23的物平面重合。

該衍射補償組件21細分為N個同樣由P_A隔開的N個補償DOE，每個補償DOE 211包括具有間隔Λ_1k的周期性相位和/或振幅光柵。從脈沖激光源S_k產生的光束在該系統的上游受到校準(所述光束例如位于平面中并且受到透鏡校準，或者直接利用與每個光源相關聯的校準透鏡而根據光束的入射角度θ_1k來設置)，并且每個光束以特定角度θ_1k到達相應的補償DOE 211。根據光束在相應的補償DOE上的入射角度θ_1k和補償DOE在z軸上的傾斜角度Θ_k(我們使Λ_1(k-1)≠Λ_1k≠Λ_1(k+1)，但是使Λ_1(-k)＝Λ_1(+k))來計算每個間隔Λ_1k，使得在中心波長λ₀，所有的激光束在離開補償DOE時是平行的，也即，在中心波長λ₀，離開補償DOE的脈沖的波矢量是全部相同的。這些DOE 211的中部位于同一平面上，該平面位于透鏡陣列22的f₁處。

傅里葉透鏡23操作從平面A至組合DOE 1的平面的傅里葉變換；因此，脈沖在組合DOE上的入射角度θ_2k由下式給出：

θ_2k＝k.P_A/f₂。

如前文所指出的，這些角度θ_2k還相關于組合DOE 1的光柵的周期，以獲得理想的最優組合。

如圖5a所示，為了使在組合DOE 1上的入射脈沖的能量的空間分布平行于組合DOE的平面(圖中的平面xOy)，在透鏡23之前的脈沖的能量分布的傾斜角度(在xOz平面)必須等于θ_2k。為了優化在組合DOE 1的水平的脈沖的重疊，由透鏡陣列22和傅里葉透鏡23組成的具有γ＝-f₂/f₁的放大率的成像設備然后將以下條件加至在離開每個補償DOE 211時能量的空間分布的傾斜角度上：

此外，認為每個補償DOE 211包括具有均勻的間隔Λ_k的光柵，以及每個補償DOE的法線相對于所期望的離開DOE 211時的傳播方向(圖5a、5b和5c中的z軸)傾斜的角度為Θ_k。光源S_k的入射方向與所期望的從DOE離開時的傳播方向之間的角度指定為θ_1k。最后，指代從補償DOE 211離開時，在脈沖的能量的空間分布和脈沖的傳播的軸線之間的角度。進入補償DOE 211時的波矢量和從補償DOE 211離開時的波矢量不平行(除了補償DOE不傾斜的情形，也即Θ₀＝0的情形)；角度Θ_k,、θ_1k和由下式聯系起來：

對在組合DOE水平的脈沖的空間重疊的優化意味著：

這給出了標示該系統的參數之間的第一關系式：

在平面A中的光源點的空間周期P_A，

光源的標號k，

脈沖的中心波長λ₀，

成像設備的放大率γ，

傅里葉透鏡23的焦長f₂。

此外，如圖5c所示，對于每個補償DOE 211，其光柵的間隔Λ_1k根據入射的方向θ_1k、光柵的傾斜的方向以及波長λ₀而由下式來建立：

最后，如果在系統的參數之間的下述關系得到滿足，則借助于在圖4和圖5a中所描述的系統而確保了對在重組DOE 1的水平的脈沖的空間重疊的優化：

即：

現在來考慮對色散的補償。

對于第一近似，將組合DOE認為是N個正弦光柵的疊加(N為待組合的光束的數量)，其間隔Λ_2k由下式給出：

組合DOE的光柵的周期因此等于：

λ₀/sinθ₂₁。

其中，θ_2k為標號為k的光束在中心波長λ₀的在組合DOE 1上的入射角度。要解決標號為k的光束的色散的補償，僅考慮標號為k的光柵。考慮波長為λ₀+δλ₀的光束以角度θ_2k+δθ_2k而入射在組合DOE 1上。如圖6b所示，為了使在λ₀和λ₀+δλ₀的受到DOE 1衍射的光束具有平行的傳播方向(或波矢量)，波矢量的正切于DOE的平面的成分的保留意味著：

因此，組合DOE 1的色散等于：

同樣地，對于補償DOE 211，可以看出，補償光柵的間隔Λ_1k根據入射的方向θ_1k、光柵的傾斜的方向以及波長λ₀而由下式來建立：

對在波長λ₀和λ₀+δλ₀受到補償DOE 211衍射的并且示出在圖6a中的波矢量之間的角度偏差δθ_1k的計算給出：

因此，補償DOE 211的角度色散等于：

通過對具有橫向放大率γ的偏離中心的成像設備的角放大率(例如圖5a中所描述的系統的橫向放大率)進行計算來推導顏色補償條件。因而獲得了下述條件：

最后，如果下述關系得到滿足，則能夠借助于圖4和圖5a中所描述的設備而確保對組合DOE 1的色散的補償。

根據在先前部分中建立的條件，如果下述關系式得到滿足，則能夠借助于在圖4和圖5a中所描述的設備來確保對組合DOE 1的色散和在組合BOE 1的水平的脈沖的空間重疊的缺陷的同時補償：

讓我們來考慮下述情形中的示例：

要組合根據為2mm的周期P_A而共線地設置的101個超短(300ps)的脈沖光源(NB：下述計算等價于在2維設置中在最大直徑上具有101個光源的情形，即在六邊形鑲嵌形式下具有7651個光源的情形)。

成像系統的放大率固定為γ＝-5。

中心波長為λ₀＝1030nm。

圖7表示了在補償DOE上的入射角度θ_1k-Θ_k的值和補償DOE 211的傾斜角度Θ_k的值，這些值滿足上述系統，并且因此確保了對組合DOE 1的色散效應和在組合DOE上的脈沖的空間重疊缺陷的同時補償。

根據本發明的具體實施方案(其示例顯示在圖8a和圖8b中)，補償DOE 211位于同一個平面，從而簡化了系統，并且尤其避免了用于對每個DOE 211定向的設備，這些設備占據大量體積并且增加了整個系統的成本。這是這樣的情形：光柵例如制造在同一個支持物上，從而展現出在制造時間和成本方面的優點。這然后體現在之前的補償DOE的傾斜角度Θ_k為零度的關系式中：Θ_k＝0。

然后對于每個補償DOE 211，光束的入射角度θ_1k為：

-當相比于顏色補償的損失而更期望有利于對重組的脈沖的重疊的缺陷進行補償時，γ.tan(k P_A/f₂)＝sin(θ_1k)(圖8a)，或者

-當相比于重疊缺陷的補償的損失而更期望有利于對重組的脈沖的顏色進行補償時，γ.tan(k P_A/f₂)(1+tan(k P_A/f₂)²)＝sin(θ_1k)(圖8b)。

補償DOE的光柵有益地為閃耀相位光柵。可替選地，他們可以是具有正弦連續輪廓的相位光柵、具有二元輪廓的相位光柵或者具有二元輪廓(黑和白)或不具有灰度的強度光柵。所有這些示例(除了閃耀光柵)展示出多重衍射級，且因此不利于系統的整體效率。

盡管在附圖的示例中，組合DOE 1和補償DOE 211以透射方式工作；當利用反射方式的DOE時，根據本發明的系統的原理仍然適用。