一種門座式起重機微弱振動信號的幅值檢測方法與流程

本發明屬于港口設備門座式起重機故障診斷技術領域，特別是涉及一種門座式起重機微弱振動信號的幅值檢測方法。

背景技術：

在門座式起重機關鍵部件(如提升機構、變幅機構和旋轉機構等)發生早期故障時，其振動信號中的有效成分異常微弱，常淹沒于強烈的背景噪聲和起重機不規則振動中。因此，如何從強噪聲背景下檢測出有效的微弱信號特征信息，已成為門座式起重機早期故障診斷的關鍵問題之一。總體而言，目前微弱信號檢測主要集中在兩大方向：一是利用信號處理的方法對噪聲進行抑制或消除，如小波分析、自適應分解、高階譜等等。然而，當噪聲頻率與信號頻率相等或相接近時，在抑制噪聲的同時有用信號不可避免的受到損害，這極大地影響微弱信號特征的提取效果；二是利用某些非線性系統自身的特性對微弱信號進行檢測，目前應用較多的非線性方法有隨機共振法、混沌振子法和差分振子法等，其中混沌振子和差分振子適用于檢測頻率已知的場合，而隨機共振適用于檢測頻率未知的情況。

隨機共振系統就是一個非線性雙穩系統，它突出了信號、噪聲及非線性系統三者之間的某種最佳匹配和協同作用，其本質是輸入信號與噪聲的協作效應，是噪聲能量轉化為信號能量的結果。混沌振子利用非線性系統對初始條件的敏感性，依據相平面軌跡是否能從混沌狀態躍變到大尺度周期狀態來判斷待檢測頻率的存在與否。差分振子和混沌振子均是利用非線性動力系統對初值的敏感性及對噪聲免疫力進行微弱信號檢測。但混沌振子法需要解一個非線性微分方程，必須進行大量的數值積分運算,因此妨礙了它在在線監測中的應用，而差分振子法只需解一個差分方程組,運算量較混沌振子法小很多。

差分振子法作為一種可視化的檢測方法，差分方程構造檢測器，確定系統激勵頻率f_e及檢測頻率f_d，通過辨識差分振子輸出相圖的狀態來判定輸入的測試信號中是否存在待檢測頻率。若差分振子相圖收斂于極環，則說明待檢測信號中存在待檢測頻率f_d。若差分振子相圖收斂于極點，則說明待檢測信號中不存在待檢測頻率f_d或待檢測信號噪聲過于強烈，差分振子系統無法檢測出待檢測信號中是否存在待檢測頻率f_d。

然而，目前基于差分振子的微弱信號檢測主要集中于利用差分振子相圖的差異檢測特有頻率成分的有無，或利用相圖的大小定性表征微弱信號幅值的大小，而無法對所包含的微弱信號的幅值進行定量檢測。

技術實現要素：

本發明的目的在于提供一種門座式起重機早期故障微弱振動信號的幅值檢測方法，該方法通過添加與微弱振動信號相同頻率、完全反相的逆向信號實現微弱周期信號的逆向幅值精確檢測，克服了現有差分振子檢測微弱信號時無法定量表征幅值的缺陷。

為了實現上述目的，本發明采用的技術方案如下：

一種門座式起重機微弱振動信號的幅值檢測方法，包括以下步驟：

1)將采集的門座式起重機的原始振動信號的數字信號輸入預先建立的差分振子系統，繪制差分振子相圖；

2)將上述差分振子相圖歸一化處理，判斷原始振動信號中是否有待檢測頻率信號；

3)若有待檢測頻率信號，在待檢測頻率信號中加入一與待檢測頻率信號相同頻率的逆向信號將信號T₂＝T₁+n(t)+G₁輸入上述差分振子系統，繪制差分振子相圖；以該差分振子相圖最小外接正方形的邊長作為指標，定量表征差分振子相圖的大小，控制在0到180度區間變化，每一變化間隔為1度，差分振子相圖最小時對應的值，即為微弱振動信號T₁的相位

其中，待檢測頻率信號T＝T₁+n(t)，n(t)為干擾成份，微弱振動信號A₁為微弱振動信號T₁的幅值，f_d是待檢測頻率，為微弱振動信號T₁的相位；為逆向信號G₁的相位，t表示時間；

4)依據微弱振動信號的相位向待檢測頻率信號中加入一個與微弱振動信號相同頻率、相同相位的逆向信號G₂，構造如下信號：

調節逆向信號G₂的幅值A₂并同時觀察差分振子系統輸出差分振子相圖，差分振子相圖達到最小時的幅值A₂即為微弱振動信號T₁幅值A₁。

本發明利用差分振子系統檢測出微弱振動故障信號后，利用調節逆向添加的相同頻率的信號G₁中的相位確定微弱振動信號T₁的相位利用調節逆向添加的相同頻率、相同相位的信號G₂的幅值A₂確定微弱振動信號T₁的幅值A₁，從而可自動實現在微弱振動信號中幅值的定量檢測，從而檢測出門座式起重機中的早期微弱故障特征信號，提早發現故障隱患，適用于檢測已知頻率的微弱信號的幅值，進而判斷設備是否發生故障。

附圖說明

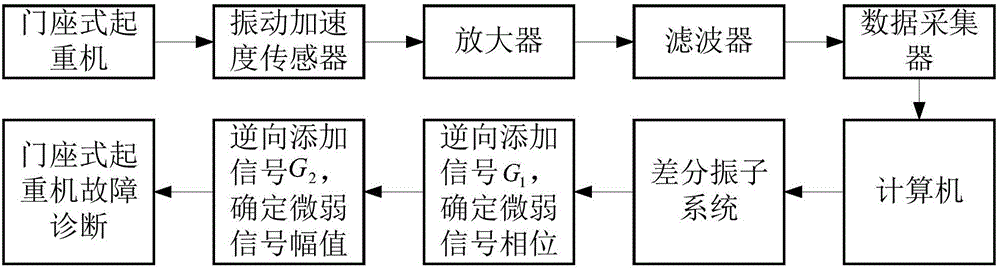
圖1是本發明的微弱振動信號的幅值檢測的整體工作原理圖；

圖2是本發明的微弱振動信號的幅值檢測的流程圖；

圖3是本發明實現的檢測含噪仿真信號是否含有30Hz頻率成分時的差分振子相圖(幅值A＝0.75)；

圖4是本發明實現的檢測含噪仿真信號是否含有30Hz頻率成分時的差分振子相圖(幅值A＝1.0)；

圖5是本發明實現的檢測含噪仿真信號是否含有30Hz頻率成分時的差分振子相圖(幅值A＝1.25)；

圖6是本發明實現的原始信號幅值變化與差分振子相圖大小的關系曲線；

圖7為本發明實現的差分振子相圖大小隨相位變化的趨勢；

圖8為本發明實現的差分振子相圖大小隨相位變化的趨勢(局部放大圖)；

圖9為本發明實現的差分振子相圖大小隨幅值A₂變化的趨勢。

具體實施方式

下面，結合實例對本發明的實質性特點和優勢作進一步的說明，但本發明并不局限于所列的實施例。

參見圖1-2所示，一種門座式起重機微弱振動信號的幅值檢測方法，包括以下步驟：

將采集的門座式起重機的原始振動信號的數字信號輸入差分振子系統，繪制差分振子相圖；

將上述差分振子相圖歸一化處理，判斷原始振動信號中是否有待檢測頻率信號；

若有待檢測頻率信號，在待檢測頻率信號中加入一個與待檢測頻率信號相同頻率的逆向信號將信號T₂＝T₁+n(t)+G₁輸入上述差分振子系統，繪制差分振子相圖；以該差分振子相圖最小外接正方形的邊長作為指標，定量表征差分振子相圖的大小，控制在0到180度區間變化，每一變化間隔為1度，差分振子相圖最小時對應的值，即為微弱振動信號T₁的相位此時

其中，待檢測頻率信號T＝T₁+n(t)，n(t)為干擾成份，微弱振動信號A₁為微弱振動信號T₁的幅值，f_d是待檢測頻率，為微弱振動信號T₁的相位；為逆向信號G₁的相位，t表示時間；

依據檢測出的微弱振動信號的相位向待檢測頻率信號中加入一個與微弱振動信號相同頻率、相同相位的逆向信號G₂，構造如下信號：

其中，逆向信號G₂與微弱振動信號T₁的頻率、相位相同，逆向信號G₂的幅值A₂在[0，max(T)]范圍內可調，調節逆向信號G₂的幅值A₂并同時觀察差分振子系統輸出差分振子相圖，差分振子相圖達到最小時的幅值A₂即為微弱振動信號T₁幅值A₁，此時A₂＝A₁。

通過以上步驟，檢測出了微弱振動信號T₁幅值A₁的大小后，即可實現判斷出門座式起重機存在設備故障，并確定設備的故障部位以及故障程度。

需要說明的是，本發明中，所述原始振動信號，可以是通過安裝在門座式起重機的提升機構、變幅機構和旋轉機構等關鍵部件(關鍵部件如提升機構的減速器及滾筒支撐軸承座、變幅機構的減速器及齒輪齒條的軸承座、旋轉機構的大型回轉支承和驅動小齒輪等)上的壓電式振動加速度傳感器采集，在提取了門座式起重機的振動信號，由數據采集儀將該信號放大濾波后進行模數轉換，從而得到所述的數字信號，可以存儲至計算機中按上述的方法步驟，由計算機程序自動進行處理，從而可自動實現檢測出是否存在包含待檢測頻率的微弱振動信號，并檢測出微弱振動信號T₁幅值A₁的大小，從而可以實現判斷出門座式起重機存在設備故障，并確定設備的故障部位以及故障程度。

本發明中，所述將差分振子相圖歸一化處理判斷原始振動信號中是否存在待檢測頻率信號，即振子相圖的橫縱坐標均在[-1,1]內,然后以原點為圓心，以0.2為半徑畫圓，落入到圓域中點的個數記為n₁；若n/N＞0.1(N為差分振子相圖總的點數，下同)則相圖收斂于極點，即可判斷原始振動信號中不存在待檢測頻率信號；若n/N＜0.02則相同收斂于極環，即可判斷原始振動信號中存在待檢測頻率信號。

需要說明的是，本發明中，所述差分振子系統可以是根據被測門座式起重機提升機構、變幅機構和旋轉機構的傳動結構及零部件的幾何參數確定被測振動信號中可能包含的故障特征頻率而建立，差分振子系統為二維離散線性系統，差分振子數學模型如下：

x_k+1＝ax_k+by_k (1)

式中a、b、c和d是系統參數，p是放大倍數，f_e是系統激勵頻率，T(k)為待檢測信號，f_d是待檢測頻率，f_s是待檢測信號的采樣頻率。

其中，系統參數一般設置為：a∈(0,0.05)、b∈(0.95,1.05)、c＝-1和d＝-1，放大倍數p∈(1,5)，系統激勵頻率根據系統參數計算得到，計算方法為待檢測信號的采樣頻率為f_s∈[50,10000]，待檢測頻率f_d的范圍取決于采樣頻率f_s，二者關系為為

具體計算時，一般可設置為a＝0.005，b＝1.004，c＝-1，d＝-1，設定好差分振子系統參數后，將待檢測信號T(k)輸入到差分振子系統中，計算得到兩個時間序列{x_k}和{y_k}，進而可繪制出差分振子的相圖。

圖3為含噪仿真信號T＝A·sin(2π·30·t)+noise輸入差分振子后得到的相圖。

其中A為周期性信號的幅值，noise為為隨機高斯白噪聲。利用差分振子對這一信號進行檢測，參數設置如下：待檢測頻率f_d＝30Hz；放大倍數p＝1；激勵頻率f_e＝0.33，系統初始值x(1)＝10、y(1)＝10。改變信號的幅值A，得到不同的差分振子輸出相圖，如圖3至圖5所示。其中，圖3為幅值為0.75時的差分振子輸出相圖，圖4為幅值為1.0時的差分振子輸出相圖，圖5為幅值為1.25時的差分振子輸出相圖。

從圖3至圖5的對比中可以看出，隨著信號幅值的增大，差分振子的相圖也隨之不斷地增大。若以差分振子相圖最小外接正方形的邊長作為指標來定量表征差分振子輸出相圖的大小(如3至圖5中的實線正方形)，則差分振子檢測信號幅值的增加與正方形邊長的增加具有單調遞增的線性比例關系，在此分析中檢測信號的幅值，每增加0.25對應的正方形邊長增加20。正方形邊長與信號幅值的關系如圖6所示。

在差分振子各參數設置相同的條件下，差分振子相圖的大小反映了信號幅值的大小。在無法確定信號幅值與差分振子相圖大小的比例關系的條件下，傳統方法無法獲得待檢測信號的精確幅值，盡管可以獲得待檢測信號幅值的相對大小，即差分振子相圖大者，其表征的幅值也較大。

在實際的故障診斷中，尤其是對設備的劣化過程進行檢測的過程中，需要對信號的幅值變化進行監測。差分振子作為一個線性離散二階系統，當系統參數固定之后，具有線性疊加性，而差分方程反映了差分振子檢測器的本質規律，因此，可以用來對微弱信號的幅值進行表征。

設輸入信號是由單一頻率的信號和噪聲組成的序列，表示成如下形式

T(k)＝s(k)+n(k) (3)

式中，n(k)表示噪聲。

設由單一頻率的信號s(k)引起的輸出為x_k(其中k＝1,2,…,N，N為輸入信號序列的長度，以下同)，由噪聲n(k)引起的擾動輸出為Δx_k，則由輸入信號T_(k)引起的輸出為(x_k+Δx_k)，代入到差分方程中則有

(x_k+2+Δx_k+2)+α(x_k+1+Δx_k+1)+β(x_k+Δx_k)＝f(k)[s(k)+n(k)] (4)

根據方程解的性質可以將上述方程轉化為以下兩個方程

x_k+2+αx_k+1+βx_k＝f(k)s(k) (5)

Δx_k+2+αΔx_k+1+βΔx_k＝f(k)n(k) (6)

因此，根據方程解的性質，若信號中有效頻率成分的幅值增加，只是影響式(5)，而不影響式(6)。換言之，在噪聲相同的條件下，方程解的變化只與信號中檢測頻率的幅值變化有關，即差分振子輸出相圖的變化只與檢測頻率幅值的變化有關。因此，在討論差分振子對信號的幅值表征時，只考慮檢測信號頻率的幅值變化即可。

設輸入信號是一個單一頻率的信號序列，表示為式(7)，

T(k)＝g(k) (7)

相應的差分振子方程的解為x_k，將其帶入差分振子方程中

x_k+2+αx_k+1+βx_k＝f(k)g(k) (8)

如果輸入信號的幅值增大到原來的K倍，即

T(k)＝Kg(k) (9)

設其對應的差分振子方程的解為z_k，則

z_k+2+αz_k+1+βz_k＝f(k)Kg(k) (10)

將式(8)兩端同時乘以K得

(Kx_k+2)+α(Kx_k+1)+β(Kx_k)＝f(k)Kg(k) (11)

比較(10)與(11)兩式可以得到如下結論

z_k＝Kx_k (12)

可見，輸入信號的幅值增大了K倍，則差分方程的解也相應地增大了K倍，亦即差分方程輸出的相圖整體增大了K倍。

基于上述分析，本發明提出在原始含噪信號中增加一逆向信號，使原始含噪信號和逆向信號的幅值進行對消，差分振子輸出相圖的尺寸必將會變小，若原始含噪信號有效成分的幅值和反相信號的幅值相等時，差分振子相圖將達到最小。基于此，本發明提出了微弱振動信號的差分振子逆向幅值檢測方法。

設有如下輸入信號

其中：A₁是輸入信號的幅值，f_d是輸入信號的頻率，φ₁是輸入信號的相位角。設n(t)是除待檢測特征信號之外的其他干擾，即待檢測信號為T＝T₁+n(t)。在待檢測信號T中再加入一個與特征信號頻率相同的信號G₁。

此時信號將變為

上式中，若則信號T₁和G₁將產生對消，此時信號T₂＝T+G₁中頻率f_d對應的幅值將達到減小，將信號T₂輸入到差分振子系統中，差分振子的相圖也將減小。相位將嚴重影響信號T₁和G₁將產生對消效果，欲精確檢測微弱信號中有效頻率的精確幅值，必須確定該頻率的相位。

設逆向信號G₁中的是可調的，控制相位在0到180度區間變化，每一個變化間隔為1度。當時，T+G₁中頻率f_d的幅值是將達到最小，差分振子相圖亦將達到最小，故差分振子輸出相圖達到最小時對應的值，滿足從而確定了待檢測信號T中頻率f_d的相位

設有如下仿真信號：

T＝T₁+n(t)＝5·sin(2π·t·60+π/3)+n(t) (16)

對應的逆向信號為

調節從0到180度每1度變化一次，構造一系列不同相位的疊加信號T+G₁，將其輸入到差分振子系統中。差分振子的系統參數設置為：c＝-1，d＝-1，f_e＝0.3310，f_d＝60Hz，x(1)＝20,y(1)＝20，用最小外接正方形去度量每個差分振子相圖的尺寸，并將其作為該相圖大小的定量表征。由此，可得到不同相位下差分振子相圖的大小，進而得到差分振子相圖大小隨相位變化的趨勢，結果如圖7所示，局部放大圖如圖8所示。

圖7中相位角從0到180度，差分振子相圖大小的變化情況，可見其中存在一個極小值，該極小值對應的相位即為原始信號T中的相位圖8是圖7的局部放大，從圖中可清晰地看到，該線的最低點(即極小值)對應的相位為60°(即π/3)，與信號T中預設的相位值是相等的。

如前所屬，特征頻率幅值的變化會引起差分振子相圖的變化，幅值越大相圖就越大。換言之，當幅值為0時，差分振子輸出的相圖是最小的。基于此，在確定原始信號T中的相位之后，本發明利用如下方法進一步檢測信號T中的幅值A₁。

利用前述確定的待檢測信號T中的相位可進一步構造如下信號：

該信號中，信號T和G₂的頻率f_d及相位均相同，而信號G₂的幅值A₂是可調的。若A₂調節至與A₁相等，即A₂＝A₁時，信號T+G＝n(t)，將其輸入差分振子，差分振子的相圖將達到最小。據此可以檢測原始信號T中的幅值A₁。

仍選用式(16)所示信號T，增加其逆向信號G₂后，得：

T₂＝T+G＝5·sin(2π·t·60+π/3)+n(t)-A₂·sin(2π·t·60+π/3) (19)

其中，A₂是連續可調的，設置A₂從0到max(T)每隔0.2變化一次，構造一系列不同幅值A₂的疊加信號T+G₂，并將其輸入到差分振子中。差分振子的系統參數設置為：c＝-1，d＝-1，f_e＝0.3310，f_d＝60Hz，x(1)＝20,y(1)＝20。可得到不同幅值A₂下差分振子相圖的大小，進而得到差分振子相圖大小隨幅值A₂變化的趨勢，結果如圖9所示。

在圖9中，當A₂＝5時，差分振子相圖最小外接正方形的邊長達到極小值，亦即此時輸入的信號T+G₂中60Hz頻率成分的幅值也達到最小。欲提高幅值A₂的檢測精度，可將設置A₂從0到max(T)之間變化的幅度進一步減小。圖9中最低點所對應的A₂和原始信號T中幅值A₁十分接近或者說基本相等。從而本發明檢測出了待檢測信號中的特征頻率f_d的精確幅值A₁。

需要說明的是，本發明在利用差分振子檢測設備故障時，需要事先確定待檢測設備的故障特征頻率。在設備傳動結構已知、軸承型號明確、設備轉速可測的情形下，可利用先驗知識計算出軸承和齒輪損傷的特征頻率，繼而建立差分振子系統，對上述特征頻率分別檢測，可確定原始振動信號中是否包含主要零部件的故障特征頻率，進而確定故障發生的具體部位。

本發明首先提出用差分振子系統來檢測微弱信號，解決了門座式起重機早期故障診斷中微弱信號幅值的定量表征的問題。

以上所述僅是本發明的優選實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護范圍。