外推追趕迭代法的MPPT算法的仿真方法與流程

本發明涉及一種外推追趕迭代法的MPPT算法的仿真方法。

背景技術：

在現在光伏發電系統中，通常要求光伏陣列的輸出功率始終保持在最大，最大功率點跟蹤(MPPT)技術就成為光伏發電系統必不可少的一個環節。MPPT就是通過實時變更系統負載特性來調整太陽能電池的工作點，最終使之在不同的溫度和日照環境下也能工作在最大功率點上。國內外知名學者提出了多種對最大功率點跟蹤的方法，最為常見的有：擾動觀察法、改進的電導增量法、開路電壓法、最大梯度法、恒定電流跟蹤法等。其中擾動觀察法和電導增量法是目前最常用的最大功率跟蹤方法。雖然以上算法在系統環境變化的條件下具有不錯的跟蹤效果，但是控制的精度往往由傳感器自身的精度所限制。例如，開路電壓法：系統的控制算法簡單，不會出現震蕩現象，穩定性較好，但是控制精度卻很低；最大梯度法：當外界環境劇烈變化，如陰影遮擋瞬間，容易造成系統控制過程對最大功率點的誤判現象，從而影響整個系統的穩定運行；擾動觀察法：控制回路采用了模塊化，跟蹤效果簡單明了，很容易實現，弊端就是不能精準地跟蹤最大功率，只能在最大功率點附近波動，這樣造成了一部分功率損失。

技術實現要素：

本發明的目的在于提供一種具有優異的穩定性、準確性和快速性的外推追趕迭代法的MPPT算法的仿真方法。

本發明的技術解決方案是：

一種外推追趕迭代法的MPPT算法的仿真方法，其特征是：包括下列步驟：

(一)采用變步長外推法為實際控制過程算法，過程如下：

第一步：給定任意步長，用梯形公式計算積分近似值

其中：T₁為梯形求積公式求得的值；a、b為區間的兩個端點；f(a)為區間端點a對應的值；f(b)為區間端點b對應的值；

第二步：按變步長外推法再次求取積分近似值。令計算此時的T_2n：

其中：h為步長；T_2n為把區間分為2n等分時，在每一個小區間內用梯形求積公式求得的值；為小區間左端點[x_i,x_i+1]的中點；n為第n等分；

第三步：對于精度控制，當且僅當|R_2n-R_n|<ε時，停止計算，取此時的R_2n為下一步的近似值，否則繼續將步長折半，轉第二步執行；

其中：R_2n為第2n等分時的誤差；R_n為第n等分時的誤差；ε為精度；

(二)采用追趕迭代法進行優化

在仿真過程中，每次對輸出功率進行迭代時，用I^k，U^k的全部分量進行乘積，求出此時的p^k，將所求值重新帶入迭代公式，求出新的I^k+1，U^k+1，p^k+1，這樣的過程使得計算時需要保留兩個近似解p^k，p^k+1，這樣對已經計算出來的信息就造成了浪費，使迭代過程步驟增加，降低運算速度；對迭代過程運用外推法進行改進，每計算出來一個新的分量便立刻用此新數據取代對應的舊數據進行迭代，則收斂速度更快，并且此時只需要存儲一個最新的數據即可；

其中：I^k為K步時的電流值；U^k為K步時的電壓值；p^k為K步時的功率值；I^k+1為K+1步時的電流值；U^k+1為K+1步時的電壓值；p^k+1為K+1步時的功率值。

步驟(一)的實際算法流程為：

第一步：開始

第二步：輸入區間的兩個端點值a,b以及要求的精度ε；測量k時刻PV光伏陣列輸出的電壓U_(k)，電流I_(k)，并計算此時的功率P_(k)；

第三步：將k賦值為1，k從1開始取值，步長h取值為b-a；為保證功率為最新采樣值P₁，利用梯形公式T₁＝(b-a)[f(a)+f(b)]/2＝h[f(a)+f(b]/2,求出此時的P₁；

第四步：采集(k+1)T時刻的電壓U_(k+1),電流I_(k+1),計算功率P_(k+1)；計算此時的△P＝P_(k+1)-P_(k)；

第五步：判斷△P≥ε？；

第六步：如若成立，將此時得電壓增量△U賦值為0，步長的初值x賦值為a+h/2，反之，此時的電壓U賦值為U+△U，步長的初值x賦值為x+h；

第七步：循環以上步驟，計算步長h＝(b-a)/2ⁱ(i＝0,1,2...),精度ε＝(b-a)[P_(k+1)+P_(k)]；

第八步：判斷此時的△P>b-a？；

第九步：如若成立，電壓增量△U賦值為-△U；反之，直接執行下一步；

第十步：U_ref(k+1)＝U_ref(k)+△U；

第十一步：返回重新采樣，輸出；

其中：P1為功率的初始值；x為步長的初始值；ε為精度；I^k為K步時的電流值；U^k為K步時的電壓值；p^k為K步時的功率值；p^k+1為K+1步時的功率值；I^k+1為K+1步時的電流值；U^k+1為K+1步時的電壓值；K為第K步；h為步長；a、b為區間的兩個端點；△P為功率的變化量；△U為電壓的變化量；U_ref(k+1)為K+1時參考電壓值；U_ref(k)為K時參考電壓值。

所述的外推追趕迭代法的MPPT算法的仿真方法，其特征是：步驟(二)的實際算法流程為：

第一步：測量第k步時的電壓U_i^k、電流

第二步：計算功率△P^k，△U＝U_i^k+1-U_i^k；

第三步：對于變量i＝1,2,3...的取值執行追的過程；

第四步：判斷△P^k<0？；

第五步：如若成立，判斷此時U_i^k+1>U_i^k？；

第六步：如若同時滿足第四、第五步則執行U_ref^k+1＝U_ref^k-△U；否則執行U_ref^k+1＝U_ref^k+△U；

第七步：對于變量i＝n-1,n-2,n-3...進行取值，對變量i執行趕的過程；

第八步：重新對電壓U^k,電流I^k進行賦值；

第九步：返回，并輸出；

其中：I^k為K步時的電流值；U^k為K步時的電壓值；p^k為K步時的功率值；I^k+1為K+1步時的電流值；U^k+1為K+1步時的電壓值；p^k+1為K+1步時的功率值；K為第K步；△U為電壓的變化量；△P為功率的變化量；U_ref(k+1)為K+1時參考電壓值；U_ref(k)為K時參考電壓值；a、b為區間的兩個端點；ε為精度。

本發明與常用的控制算法實現的仿真圖和數據進行細致分析和比較，具有優異的穩定性、準確性和快速性。

附圖說明

下面結合附圖和實施例對本發明作進一步說明。

圖1是變步長外推法流程圖。

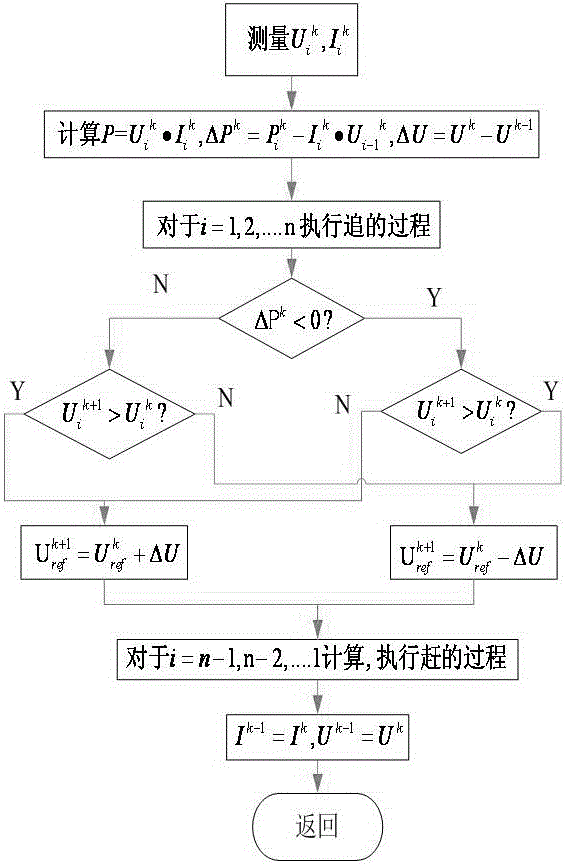
圖2是追趕迭代法控制流程圖。

圖3是光伏電池的仿真圖。

圖4、圖5分別是擾動觀察控制算法搭建模型圖、外推追趕迭代控制算法搭建模型圖。

圖6、圖7分別是擾動觀察法輸出功率圖、外推追趕迭代法輸出功率圖。

圖8、圖9分別是擾動觀察法輸出功率局部放大圖、外推追趕迭代法輸出功率局部放大圖。

圖10是100KW光伏系統的仿真圖。

圖11是給定光照強度的變化曲線圖。

圖12是擾動觀察法功率輸出圖。

圖13是變步長外推追趕迭代法功率輸出波形圖。

具體實施方式

一種外推追趕迭代法的MPPT算法的仿真方法，包括下列步驟：

(一)采用變步長外推法為實際控制過程算法，過程如下：

第一步：給定任意步長，用梯形公式計算積分近似值

其中：T₁為梯形求積公式求得的值；a、b為區間的兩個端點；f(a)為區間端點a對應的值；f(b)為區間端點b對應的值；

第二步：按變步長外推法再次求取積分近似值。令

計算此時的T_2n：

其中：h為步長；T_2n為把區間分為2n等分時，在每一個小區間內用梯形求積公式求得的值；為小區間左端點[x_i,x_i+1]的中點；n為第n等分；

第三步：對于精度控制，當且僅當|R_2n-R_n|<ε時，停止計算，取此時的R_2n為下一步的近似值，否則繼續將步長折半，轉第二步執行；

其中：R_2n為第2n等分時的誤差；R_n為第n等分時的誤差；ε為精度；

(二)采用追趕迭代法進行優化

在仿真過程中，每次對輸出功率進行迭代時，用I^k，U^k的全部分量進行乘積，求出此時的p^k，將所求值重新帶入迭代公式，求出新的I^k+1，U^k+1，p^k+1，這樣的過程使得計算時需要保留兩個近似解p^k，p^k+1，這樣對已經計算出來的信息就造成了浪費，使迭代過程步驟增加，降低運算速度；對迭代過程運用外推法進行改進，每計算出來一個新的分量便立刻用此新數據取代對應的舊數據進行迭代，則收斂速度更快，并且此時只需要存儲一個最新的數據即可；

其中：I^k為K步時的電流值；U^k為K步時的電壓值；p^k為K步時的功率值；I^k+1為K+1步時的電流值；U^k+1為K+1步時的電壓值；p^k+1為K+1步時的功率值。

步驟(一)的實際算法流程為：

第一步：開始

第二步：輸入區間的兩個端點值a,b以及要求的精度ε；測量k時刻PV光伏陣列輸出的電壓U_(k)，電流I_(k)，并計算此時的功率P_(k)；

第三步：將k賦值為1，k從1開始取值，步長h取值為b-a；為保證功率為最新采樣值P₁，利用梯形公式T₁＝(b-a)[f(a)+f(b)]/2＝h[f(a)+f(b]/2,求出此時的P₁；

第四步：采集(k+1)T時刻的電壓U_(k+1),電流I_(k+1),計算功率P_(k+1)；計算此時的△P＝P_(k+1)-P_(k)；

第五步：判斷△P≥ε？；

第六步：如若成立，將此時得電壓增量△U賦值為0，步長的初值x賦值為a+h/2，反之，此時的電壓U賦值為U+△U，步長的初值x賦值為x+h；

第七步：循環以上步驟，計算步長h＝(b-a)/2ⁱ(i＝0,1,2...),精度ε＝(b-a)[P_(k+1)+P_(k)]；

第八步：判斷此時的△P>b-a？；

第九步：如若成立，電壓增量△U賦值為-△U；反之，直接執行下一步；

第十步：U_ref(k+1)＝U_ref(k)+△U；

第十一步：返回重新采樣，輸出；

其中：P1為功率的初始值；x為步長的初始值；ε為精度；I^k為K步時的電流值；U^k為K步時的電壓值；p^k為K步時的功率值；p^k+1為K+1步時的功率值；I^k+1為K+1步時的電流值；U^k+1為K+1步時的電壓值；K為第K步；h為步長；a、b為區間的兩個端點；△P為功率的變化量；△U為電壓的變化量；U_ref(k+1)為K+1時參考電壓值；U_ref(k)為K時參考電壓值。

所述的外推追趕迭代法的MPPT算法的仿真方法，其特征是：步驟(二)的實際算法流程為：

第一步：測量第k步時的電壓U_i^k、電流

第二步：計算功率△P^k，△U＝U_i^k+1-U_i^k；

第三步：對于變量i＝1,2,3...的取值執行追的過程；

第四步：判斷△P^k<0？；

第五步：如若成立，判斷此時U_i^k+1>U_i^k？；

第六步：如若同時滿足第四、第五步則執行U_ref^k+1＝U_ref^k-△U；否則執行U_ref^k+1＝U_ref^k+△U；

第七步：對于變量i＝n-1,n-2,n-3...進行取值，對變量i執行趕的過程；

第八步：重新對電壓U^k,電流I^k進行賦值；

第九步：返回，并輸出；

其中：I^k為K步時的電流值；U^k為K步時的電壓值；p^k為K步時的功率值；I^k+1為K+1步時的電流值；U^k+1為K+1步時的電壓值；p^k+1為K+1步時的功率值；K為第K步；△U為電壓的變化量；△P為功率的變化量；U_ref(k+1)為K+1時參考電壓值；U_ref(k)為K時參考電壓值；a、b為區間的兩個端點；ε為精度。

變步長外推法的原理：

在對最大功率點控制算法的實現過程中，需要給出恰當的步長如果步長取的太大，則精度難以滿足。如果步長取的太小，將會導致控制過程中計算量的增大。在系統仿真之前給與一個恰當的步長，往往不易實現。在實際仿真中，常常采用變步長的方法，基本思想是：在步長依次減半的過程中，反復利用求積公式進行運算，直至兩次步長折半后的積分差值的絕對值|I_2n(f)-I_n(f)|<允許的精度σ，則求積過程結束，并且將最新的I_2n(f)作為新的求積近似值。將時間[a,b]進行n等分，則步長為T_n為：

如果將[a,b]區間2n等分，則步長也將變為原來的一半，則此時步長為而此時的T_2n為：

對于復合求積公式其算法是絕對收斂的，因此，用折半的方法構造出近似值的序列為T(h)，而在實際控制過程中，常常運用一個近似序列T₁,T₂,...T_n,.....，去不斷逼近精確值T,恰好序列{T_i}(i＝1,2...)又通常與區間的步長息息相關。但是，由于這種算法的收斂速度較慢，而在實際控制過程中如何提高收斂速度節省計算量成為了一個新的問題，針對這一點不足，將以上算法進行改進，推廣到更一般的情況。給定一個收斂序列使其收斂到f(0)，在此收斂數列的基礎上再構造一個新的收斂序列使其能夠更快地收斂于f(0)，這樣就使算法得到二次加速。

具體運用于本文的實現過程如下，首先對任意給定步長h進行泰勒展開：

如果此時的f'(0)≠0，那么此時逼近f(0)的階都是O(h)。現在將(3)、(4)兩個式子進行改進，得到：

如果此時f”(0)≠0，那么逼近f(0)的誤差階為O(h²)。即新序列比舊的序列f(h)更快的收斂于f(0)，以此類推，可以繼續用f₁(h)生成新的f₂(h)序列，使其更迅速地收斂于f(0)，由于

對(6)、(7)進行化簡，有：

如果此時f”'(0)≠0，那么序列{f₂(h)}逼近f(0)的誤差階就為O(h³)。

以上推理過程很好地說明了可以利用近似值推算出更加精確的近似值，是一種加速收斂的算法，而且展開次數越高，控制精度也越高。

仿真結果及數據分析

系統搭建及仿真

為實現大型光伏陣列組件的優化利用，國內外許多學者對光伏電池的建模^[10-12]及最大功率點跟蹤方法進行了廣泛研究^[13-16]。根據相應的理論分析以及控制算法框圖，首先利用Matlab軟件在Simulink環境下搭建光伏電池的數學仿真模型如圖3所示，在這里，仿真參數的選擇采取生產商提供的數據以日普生公司生產的150W太陽能電池板的參數為依據(如表1所示)。分別采用變步長外推追趕迭代法與擾動觀察法進行仿真比較。

表1：150W光伏電池參數

以上圖3及圖4和圖5分別是對光伏電池和兩種MPPT算法搭建的系統仿真模型。為了驗證該算法的優越性,在Matlab軟件中搭建規模為2×2的光伏陣列，其在標準情況下最大功率為600W。為了研究光照變化對其輸出功率的影響，做以下仿真分析：光照強度在0.5s時從1000W/m2突然降低為600W/m2。

圖6、圖7為仿真結果輸出，由圖6、圖7可知，變步長外推追趕迭代法不管在系統運行開始時還是在光照強度突變時，其最大功率跟蹤效果都比擾動觀察法更具優勢。

圖8、圖9為功率局部放大圖，表明了外推追趕迭代法能夠在跟蹤到最大功率點后穩定在最大功率點處工作，而擾動觀察法卻在最大功率點處不斷震蕩，造成部分功率損失。綜上，本文提出的算法能很好的改善系統穩定性，具有快速的跟蹤效果。

最后，為了驗證該算法能夠適應不同環境變化，將該控制算法應用到整個光伏發電系統中進行系統仿真。為了更好地驗證該算法的優越性，搭建了100KW光伏并網發電系統仿真模型，如圖10所示。

仿真結果及分析

分別采用擾動觀察法與變步長外推追趕迭代法進行仿真比較，圖11是給定光照強度，首先模擬光照強度逐漸降低(升高)，直至光照達到最低(高)值，然后模擬由于陰影或天氣突變導致的光照突然下降(升高)時系統對最大功率的跟蹤過程。

由圖12功率輸出波形很容易看出，擾動觀察法的控制雖然簡單，算法也通俗易懂，而且對硬件設施的要求也不高，實現過程比較方便，其不足主要如下：對于擾動觀察法，其最難控制的問題往往在于擾動步長的設定，步長過長，系統的跟蹤速度很快，但當光照強度發生劇烈變化時最大功率點也會發生較大的波動，即使光照強度均勻變化，輸出功率變化過程也有所波動，仍有一些弊端亟待解決。

仿真圖及數值分析表如下所示：圖12為擾動觀察法下的最大功率點輸出波形，對應的表2為迭代輸出的具體數值。

表2擾動觀察法功率輸出

由表2很清楚地看出，對于擾動觀察法系統會在最大功率點(MPP)處劇烈震蕩，會造成功率的大量損耗，雖然減小擾動步長，會使得系統在MPP的震蕩降低，這樣帶來的不利因素就是系統跟蹤MPP的速度變慢，系統反應變得遲鈍。當光強發生較大變化時，擾動觀察法會發生對系統的誤判，誤判帶來的直接后果就是導致整個系統出現劇烈、大幅度震蕩，直至母線電壓崩潰。

對比圖12，圖13功率P/W實時跟蹤仿真曲線很容易看出，對于整個光伏系統擾動觀察法需要0.5s才完全進入穩定運行狀態，而變步長外推追趕迭代法只需要0.35s就實現了穩態運行且啟動過程震蕩很小。速度遠遠快于擾動觀察法的啟動速度，即使光照突變，系統對最大功率點的跟蹤也幾乎沒有震蕩。當光照強度逐漸增加(逐漸減少)時，功率也隨之平穩增大(平穩減小)，當光照強度突然增加(突然減小)時，系統能夠迅速反應，使功率輸出也迅速增大(降低)，重新回到此時光照強度輸出的最大功率點上。

表3變步長外推追趕迭代法功率輸出結果

對比表2，表3仿真數據輸出結果易得，擾動觀察法要想達到與外推追趕迭代法相同的精度要求需要8次迭代才能實現，而外推追趕迭代法迭代次數很少，僅僅需要4次迭代就能完全達到跟蹤精度和控制要求。

通過對上述兩種方法的仿真數據進行分析，可以看出兩種方法的最優值是相同的，這保證了系統跟蹤的精準性。很明顯變步長外推追趕迭代法的迭代次數明顯少于擾動觀察法，從而提高了整個系統的工作效率。

與原有的算法相比具有以下幾點優點：

該算法是一種加速收斂的算法，可以避免由于瞬時物理量檢測時給系統帶來的擾動，降低對系統硬件的依賴，從而保證系統運行時的穩定性，確保跟蹤速度的同時，可以提高精度。

將該算法應用于100KW光伏發電系統中，根據仿真結果很容易看出，整個光伏系統只需要0.35s就已經進入穩態運行狀態，速度遠遠超過擾動觀察法的啟動速度。

隨著光照強度的變化對最大功率點有很好的跟蹤效果，即使光照突變也幾乎沒有震蕩。證明了該算法不僅具有擾動觀察法的優點，而且具有響應速度快，迭代次數少等優點。達到了預期的設計目的,無論在跟蹤速度上還是在跟蹤精度都表現出了很明顯的優越性，具有很好的應用和推廣價值。