一種全鋼子午線輪胎的胎體安全倍數計算方法與流程

本發明涉及全鋼子午線輪胎的胎體安全倍數計算領域，尤其涉及一種利用輪胎材料模型及有限元分析技術進行全鋼子午線輪胎的胎體安全倍數的計算方法。

背景技術：

隨著我國汽車工業的快速發展，汽車行業對輪胎的性能和品質的要求越來越高。高品質輪胎應具有優越的安全性能、耐久性能和高速性能。全鋼子午線輪胎與傳統的斜膠輪胎相比，由于其滾動阻力低，節省燃料且耐磨、耐刺，安全性能高，已成為輪胎產業的主流產品。據公安部門統計，2013年全國大中型客車數量達249萬輛，貨車數量達2016萬輛，貨車增加116萬輛。由于大中型客貨車拉載人員多、貨物量大，一旦發生交通事故往往造成重大人員傷亡和財產損失，是道路交通事故預防重點和難點。目前汽車輪胎爆胎、疲勞駕駛與超速行駛已經并列成為道路交通安全的三大殺手，輪胎作為汽車結構的重要組成部分，其安全性在營運車輛交通安全中的位置尤為突出。因而輪胎各部位的安全倍數計算式輪胎結構設計的必要組成部分。

子午線輪胎自問世以來已經有半個多世紀了，它以獨特的結構帶來了優異的性能，在輪胎發展歷程中，其結構大致可分為兩種：斜交輪胎結構和子午線輪胎結構。與此相適應，作為輪胎結構設計理論基礎的輪胎力學也可以分為斜交輪胎結構力學和子午線輪胎結構力學。由于子午線輪胎的性能更加依賴合理的結構設計，輪胎的結構力學模型的到了進一步發展，這些理論模型應用于輪胎的結構設計已經充分的顯示出了力學分析在改進輪胎產品質量中的重要作用，使人們認識到結構設計與材料設計具有同等重要的地位。到20世紀80年代中期，有限元分析技術在輪胎斷面輪廓設計中的應用使得輪胎斷面輪廓設計突破了自然平衡輪廓的束縛，人們開始尋求自然輪廓之外的最佳輪廓。從而使得有限元技術在輪胎結構設計中被廣泛的應用起來，這不僅加快了輪胎新產品開發速度，同時也促進了輪胎產品的多樣化。

全鋼子午線輪胎的安全倍數數值是作為描述輪胎安全性的指標，他所關注的焦點是輪胎結構設計強度的最薄弱環節，即最小強度與最大承載條件下對輪胎工作可靠性的影響。目前我國輪胎行業習慣采用應力及強度的平均值進行計算，但與水壓爆破的實際數值相比，有很大偏差，主要原因是由于對弱點分析計算的不到位或忽視。

我國的輪胎行業的發展目前已有半個多世紀，現在的輪胎產量已經處于世界領先地位，輪胎企業也積累了較豐富的生產經驗和技術經驗，但是國內的輪胎生產力量分散，技術研發與設計水平與國外優秀企業仍有差距。隨著計算機技術的發展，日益成熟的多體系系統動力學仿真軟件在汽車行業和輪胎行業的開發設計中被越來越廣泛的應用。有限元分析的一個很大用途就是可以有效的模擬輪胎試驗。同時可以通過有限元方法來研究不同使用條件下力學特性的一般規律。

目前輪胎結構設計過程中，普遍采用基于薄膜理論的傳統安全倍數計算公式為

其中B_L單根簾線破斷力(kg/根)R_drum為成型鼓半徑(cm)，u_ends胎體簾線密度(根/cm)，P為輪胎充氣壓力(kg/cm²)，R_a、R_b、R_c分別為胎體簾線胎冠中心半徑、最大斷面寬處半徑及鋼絲圈半徑，如圖7所示，單位取cm。

全鋼子午胎胎體安全倍數的計算對于其結構設計、鋼絲的選取非常重要，輪胎的安全性及其多種質量問題與胎體安全性有關，如市場上的拉鏈爆問題、鋼絲齊斷問題以及胎里露絲和實鼓問題都與胎體的安全性、鋼絲選取等有著密切的關系，因此準確的輪胎胎體安全倍數計算對實際產品設計、產品質量有重要的指導作用。

技術實現要素：

全鋼子午線輪胎安全倍數計算是輪胎設計的重要參數之一，直接影響輪胎使用安全性，同時影響產品的病疵退賠等其他質量問題。傳統的安全倍數計算與實際水壓爆破試驗差異較大，因此研究一種新的安全倍數計算方法非常重要。

一種輪胎胎體各個單元的安全倍數計算方法，該方法采用以下的公式進行計算：

其中：B為帶束層單根簾線破斷力，單位為N/根；

L_elem為單元長度，單位為cm；

a₀為簾線密度系數；

u_ends簾布壓延密度，單位為根/cm；

E_elem單元簾線方向即周向的張應力，單位為N/cm²；

S_elem單元簾線方向橫截面積，單位為cm²；

所述的

即成型鼓半徑R_dum與單元重心半徑R_elem的比值。

一種全鋼子午線輪胎的胎體安全倍數計算方法，該方法采用所述的公式進行計算各個單元的安全倍數，輪胎帶束層整體安全倍數取其各單元安全倍數的最小值，得出輪胎帶束層整體安全倍數取值，即W＝min w_i，i＝1,2,3....n,n為胎體單元個數。

本發明以10.00R20全鋼子午線輪胎為例，利用自主研發的輪胎材料模型和結構力學有限元分析技術，胎體鋼絲/橡膠材料選取C60-225HT和C60-175W二種，氣壓分別為0.83Mpa、0.93Mpa，進行了輪胎充氣狀態及負荷加載3900kg狀態下的胎體安全倍數計算，分析輪胎在充氣及負荷狀態下安全倍數的差異及變化特點。通過水壓爆破進行試驗對比，總結設計出一套全新的胎體安全倍數計算公式。

附圖說明

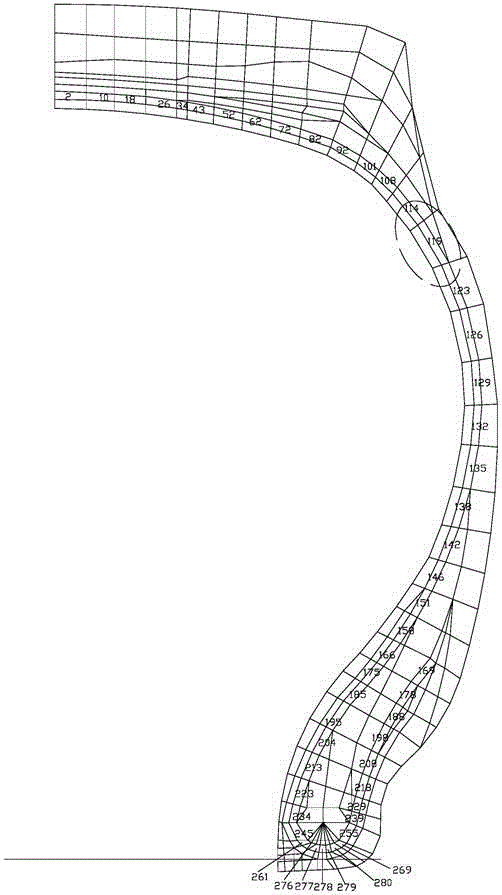
圖1全鋼子午胎某一切面的有限元網格圖。

圖2胎體某一單元的放大圖。

圖3為充氣壓力為0.83Mpa、0.93Mpa、C60-225HT胎體各單元安全倍數的變意圖。

圖4為充氣壓力為0.83Mpa、0.93Mpa、C60-175HT胎體各單元安全倍數的變化圖

圖5為充氣壓力為0.83Mpa、負荷3900kg工況下，C60-225HT胎體非接地斷面各單元的安全倍數變化圖。

圖6為充氣壓力為0.83Mpa、負荷3900kg工況下，C60-175HT胎體接地斷面各單元的全倍數變化圖。

圖7為傳統安全倍數計算胎體示意圖。

圖8為有限元分析計算求解過程。

圖9為有限元分析分析及安全倍數計算流程。

具體實施方式

1、輪胎材料模型及輪胎結構力學有限元分析概述

在這里,首先對研制輪胎結構有限元分析軟件所涉及的一些理論和技術作簡要概述。

1.1單元模型

采用了兩種單元模型:八節點六面體等插單元和六節點五面體等參單元。

1.2材料模型

橡膠材料不可壓縮性用Lagrangian乘子法解決,而其物理非線性用Mooney-Rivlin模型來模擬，應變能密度函數描述：

W(I₁,I₂)＝C₁₀(I₁-3)+C₀₁(I₂-3)

其中I1和I2分別為應變第一和第二不變量,C10和C01為由實驗確定的材料常數。

對橡膠基復合材料而言,用正交各向異性材料模型來模擬,其相應的等效彈性模量由橡膠材料和增強纖維材料的模量及體積分數用Halpin-Tsai方程確定

1.3幾何模型

對于輪胎的大變形,采用Lagrangian法進行描述,應變張量和應力張量分別取為Green-Lagrangian應變張量E和第二類Piola-Kirchhoff應力張量S可分別表示為：

其中∑為第一類Piola-Kirchhoff應力張量。在這里，Green-Lagrangian應變張量E又可以用位移表示為：

1.4平衡方程

令q0為定義在初始構形上的體積力,則用第一類Piola Kirchhoff應力張量∑表示的平衡方程為：

Div∑+q0＝0

1.5本構方程

對于彈性介質,用第二類Piola Kirchhoff應力張量S和Green-Lagrangian應變張量E表示的本構方程為：

S_ij＝D_ijklE_kl

如果四階張量D_ijkl是應變張量E的函數,則為非線性彈性；如果D_ijkl是常數張量,則是線彈性。有時非線性彈性本構方程用增量矩陣形式表示：

dS＝DT De

1.6接觸問題

輪胎與地面的接觸處理

如何處理接觸區域是輪胎結構分析的難點。輪胎與地面之間的作用是一個大變形接觸問題。接觸問題的突出特點是接觸邊界條件無法事先確定。眾所周知,線性接觸問題的解是在作了接觸區域的形狀假定和接觸力分布模式假定后得到的,這就是著名的Hertz假定。而對于非線性的大變形接觸,不可能預先了解接觸區的形狀與接觸力的分布形式。針對以上問題，采用可變約束和約束增量的概念。其基本思想是:在每一步計算執行前給出單邊位移約束的約束改變量并將其代入增量平衡方程中進行計算,隨時根據約束反力和自由節點位移來變更約束邊界。正如自由節點位移增量可以迭加一樣,約束增量也可迭加。最后的約束邊界與整體位移場一并得到；該方法的優點是計算精度高,收斂速度快。

輪胎與輪輞的接觸處理

研究文獻中很少有提及輪輞約束的,即使有也只是使用了簡單的固定約束處理手法^[6]。而在實際情形中,輪胎與輪輞之間存在著過盈配合關系,將輪胎裝到輪輞時,胎圈部將產生一個“內收”的位移和對輪輞的“緊箍”作用。由于鋼絲圈與周圍材料在模量上差異巨大,在胎圈部位將不可避免地產生一個應力集中區,這一應力集中區將對輪胎結構產生影響。另外由于胎圈部外緣形狀與輪輞基座并非是自然密合的,所以將輪胎裝在輪輞上時首先在胎圈與輪輞之間就存在大變形接觸。同時由于輪輞表面具有雙曲率結構,這一接觸問題比輪胎與地面之間的接觸更加復雜和難以處理。這里采用可變約束法來解決。這一問題是這樣進行的:將位于接觸面上每一點的約束反力分為切向和法向兩個分量,若兩者之比小于某一預先設定的數,則該點駐定不動,否則該點是滑移點,滑移量即為約束增量,與約束反力的切向分量方向相反且成正比。滑移后的點還應位于約束面內。不斷地迭代計算并調整滑移點的位置使切向力更小,當所有的約束點都駐定下來或在小范圍內游動時,便近似得到了無摩擦時的輪輞接觸邊界。

1.7輪胎結構有限元分析流程

有限元分析計算求解過程如圖8所示。

有限元分析分析及安全倍數計算流程如圖9所示。

2、有限元安全倍數的計算

有限元是近似求一般連續域問題的數值方法，是計算力學的一門分支，求解微分方程問題的一種數值方法。對輪胎而言，就是將整體輪胎離散為上萬個單元個體(如圖1，某一切面輪胎劃分的網格圖)，那么作為輪胎一部分的骨架材料胎體同樣由多個單元組成(如圖2，某一胎體單元的放大圖)，由有限元分析我們可以得到各個單元和應力場、應變場。

輪胎胎體各單元的安全倍數應該等于輪胎胎體單絲的強力與單絲實際所受張力的比值。

因此，輪胎胎體各個單元的安全倍數計算公式表示為：

其中B單根簾線破斷力(N/根)，L_elem單元周向長度(cm)，a₀簾線密度系數，u_ends簾布壓延密度(根/cm)，E_elem單元簾線方向張應力(N/cm²)，S_elem單元簾線方向截面積(cm²)。

胎體單根鋼絲的破斷力B可通過拉伸試驗獲得數據(鋼絲廠家及輪胎企業常規的測試項目)，L_elem、S_elem為網格劃分基本參數，E_elem可通過有限元力學計算獲得，其中

即成型鼓半徑R_dum與單元重心半徑R_elem的比值，反映單元位置不同簾線密度的變化。

考慮到輪胎胎體破壞首先在最薄弱點，通常發生在胎肩與胎側過渡區域，也就是輪胎拉鏈爆的部位。因此輪胎胎體整體安全倍數取其各單元安全倍數的最小值，即

W＝min w_i，i＝1,2,3....n,n為胎體單元個數。 (3)

圖3～圖6分別給出了胎體各單元在輪胎充氣壓力為0.83Mpa、0.93Mpa時的安全倍數數值，以及充氣壓力為0.83Mpa負荷在3900kg接地區域安全倍數的變化，研究了安全倍數在充氣及不同使用工況下的變化(傳統基于薄膜理論的計算只是計算充氣狀態下的安全倍數，無法進行不同使用工況下計算)。

3、測試實例

一、輪胎材料性能測試，材料模型的建立。

包括膠料、鋼絲骨架材料、鋼絲/橡膠復合材料等，建立材料性能輸入文件。

備注：鋼絲骨架材料測試即得到胎體鋼絲的破斷力B。

二、輪胎產品設計及材料分布圖繪制。

備注：本部分將得到u_ends胎體簾布壓延密度(根/cm)，a₀簾線密度系數，反映不同位置簾線(單元)簾線密度的變化。即成型鼓半徑R_dum與單元重心半徑R_elem的比值，

三、利用自主研發的仿真分析軟件對產品進行有限元分析計算。包括各種充氣計算及充氣下負荷計算等。經過前處理、計算、后處理過程，得到胎體各單元的應力、應變、位移、幾何信息等。詳見上述“有限元分析分析及安全倍數計算流程”。

備注：本部分可以得到，作為輸入參數的輪胎充氣壓力P；提取的胎體單元的幾何信息，單元長度L_elem、單元簾線方向橫截面積S_elem；有限元計算得到胎體各單元簾線方向(即經向)的張應力E_elem，至此，本發明計算的所有參數均已得到。

四、胎體安全倍數的計算

胎體各單元的安全倍數計算公式

輪胎胎體的破壞首先發生在最薄弱點，因此輪胎帶束層整體安全倍數取其各單元安全倍數的最小值。

因此輪胎胎體整體安全倍數取其各單元安全倍數的最小值，即

W＝min w_i，i＝1,2,3....n,n為胎體單元個數。

4、本發明的主要特點和技術優勢

1)輪胎力學的發展由薄膜理論、薄殼理論發展到現在的有限元分析技術，輪胎有限元分析技術是更為先進的輪胎力學分析手段，因此其計算精度大幅提升。

2)本發明基于自主知識產權的輪胎結構力學有限元分析技術和材料模型，對胎體的安全倍數計算給出了有限元算式，不僅能夠給出輪胎整體的胎體安全倍數，而且能夠給出胎體各個部位(有限單元)的安全倍數，同時還能描述不同使用工況下的安全倍數，對比傳統安全倍數計算公式有著巨大優勢，傳統安全倍數只能計算輪胎整體充氣工況的安全倍數。

3)水壓爆破試驗、有限元安全倍數計算、傳統安全倍數計算三者對比數據表明(見表1)，有限元胎體安全倍數與實際測試誤差控制在5％左右，傳統胎體安全倍數計算比實際測試值偏大10％～20％，因此，本發明大大提高了胎體安全倍數的計算精度，全鋼子午胎胎體安全倍數計算是輪胎產品設計的基本參數，本發明對行業理論研究發展具有重大意義。

表1水壓爆破試驗測試、本發明安全倍數計算、傳統安全倍數計算數值對比