一種空天飛行器機翼振動響應的快速仿真方法與流程

本發明屬于航空航天技術領域，涉及一種機翼翼型氣動彈性振動仿真技術，具體涉及一種空天飛行器機翼振動響應的快速仿真方法。

背景技術：

空天飛行器是一種可重復使用的新一代天地往返系統，對于降低空間運輸成本具有重要的意義。其特點之一是能在外太空和大氣層之間自由起落和飛行。要發展空天飛行器,就要解決以下關鍵技術:即兼具超輕質量、高強韌、耐熱和抗沖擊性能的空天器結構技術,高超聲速技術,高機動飛行技術,長距離空天飛行技術,高隱形技術,精準打擊及可靠性技術。在這些關鍵技術中，氣動彈性問題是設計、制造空天飛行器的基礎問題，而與該問題密切相關的飛行器機翼的設計則是當前的研究熱點和技術難點。

空天飛行器的機翼在高速飛行過程中的振動形式直接影響機翼結構體的強度。一般而言，機翼可能存在的振動形式包括：穩定態、極限環振動、周期振動、混沌運動和發散。機翼的設計盡量使其在整個飛行過程中處于穩定狀態。這樣對機翼結構體的強度損傷是最小的。極限環振動是指機翼做類簡諧振動。而周期振動是指機翼的振動稍微復雜但是振動幅值具有重復性。不同翼型參數和飛行速度下，機翼顫振邊界和振動形式是不同的。因此有必要對機翼顫振系統進行分析。原始的機翼模型富含積分項。因為積分項的存在，不管是對于直接的數值求解算法還是攝動法或者加權殘余法來說，求解起來都需要事先進行大量的符號處理，消耗大量的計算資源。現有的方法如諧波平衡法，攝動法等往往不能快速、全面的分析系統的響應。這很大程度上影響了機翼結構的參數設計。

技術實現要素：

本發明的目的在于提供一種空天飛行器機翼振動響應的快速仿真方法，以克服上述現有技術存在的缺陷，本發明基于時間離散法，通過在時間域的離散獲得飛行器機翼氣彈系統的代數方程，避免了一般的非線性系統分析方法中大量的符號運算，同時簡化了系統方程，使得求解效率得到較大提高。

為達到上述目的，本發明采用如下技術方案：

一種空天飛行器機翼振動響應的快速仿真方法，包括如下步驟：

1)建立空天飛行器在流固耦合下的二元機翼顫振動力學模型；

2)通過對機翼顫振動力學模型進行求解建立時間離散法代數方程組；

3)建立緊湊型的時間離散法代數方程組；

4)求解上述緊湊型時間離散法代數方程組，得到機翼系統的振動響應曲線。

進一步地，步驟1)具體為：

結合二元機翼含有線性彈簧時的氣動彈性模型，并考慮機翼系統在俯仰和沉浮兩個自由度的結構非線性，建立機翼系統方程：

其中，x_α是機翼氣彈坐標系原點到質心的無量綱距離，ξ＝h/b是無量綱沉浮量，(·)表示對無量綱時間τ的導數，τ＝Ut/b，t為時間，U^*為無量綱速度，定義為U^*＝U/(bω_α)，U為空氣來流速度，其中ω_ξ和ω_α分別是不耦合方程沉浮和俯仰自由度的固有頻率，ζ_ξ和ζ_α是阻尼比，r_α為繞彈性軸的轉矩，α是俯仰角，h是偏轉角，μ＝m/πρb²，m是機翼質量，ρ為空氣密度，b為機翼的半弦長；

M(α)和G(ξ)分別是俯仰和沉浮自由度的非線性項，表達式為：

M(α)＝α+βα³，G(ξ)＝ξ+γξ³， (3)

其中β和γ為非線性項系數；

C_L(τ)和C_M(τ)是線性氣動力和氣動力矩，表達式為：

其中Wagner函數φ(τ)為ψ₁，ψ₂，ε₁，ε₂是Wagner常數，a_h是機翼中軸線到氣彈坐標原點的無量綱距離；

然后，通過引入一組積分變換式，將上式中C_L和C_M包含的積分項消除，從而將積分微分方程轉化為微分方程組，記為如下形式：

其中，c₀＝1+1/μ，c₁＝x_α-a_h/μ，

c₃＝[1+(1-2a_h)(1-ψ₁-ψ₂)]/μ，c₄＝2(ε₁ψ₁+ε₂ψ₂)/μ，

c₅＝2[1-ψ₁-ψ₂+(1/2-a_h)(ε₁ψ₁+ε₂ψ₂)]/μ，

c₆＝2ε₁ψ₁[1-ε₁(1/2-a_h)]/μ，c₇＝2ε₂ψ₂[1-ε₂(1/2-a_h)]/μ，

其中，r_α為彈性坐標系的回轉半徑。

進一步地，步驟2)具體為：

將步驟1)得到的微分方程組(4)中的6個待求函數α(τ)，ξ(τ)，ω_i(τ)，i＝1,2,3,4，首先假設成Fourier級數形式：

其中，α_j，ξ_j，ω_j，j＝0,...,2N為相應的諧波系數；

將假設的近似解(5)代入微分方程組(4)中，得到殘差函數：

其中，R_j表示

最后，迫使殘差函數R_j在一個周期上的2N+1個等距時間點τ_i上為零即得到時間離散法代數方程組，該機翼系統含有6×(2N+1)個方程，6×(2N+1)+1個未知數。

進一步地，步驟3)具體為：

對時間離散法代數方程組的每項進行時間離散處理，對α(τ)在2N+1個時間點τ_i離散，可得：

其中θ_i＝ωτ_i，將上式寫為矩陣形式：

簡單表示為：

其中，

Q_α＝[α₀,α₁,...,α_2N]^T

類似的其中Q_ξ分別為與ξ有關的配點和諧波系數，和分別為與ω_i有關的配點和諧波系數；

然后，對在2N+1個時間點進行離散可得：

將上式寫為矩陣形式：

令矩陣

因此有：

其中

同理有：其中和分別是關于ξ和ω_j導數的配點；

然后，對在2N+1個時間點離散，有：

將上式(9)寫為矩陣形式：

上式中的方陣用FA²表示為

因此，

同理有其中和分別是關于ξ和ω_j二階導數的配點；

由此時間離散法代數方程組經變換后得到如下形式：

其中D＝FAF^-1，且

將和用表示，然后將他們代入到非線性方程中得：

其中A_1α，B_1ξ，A_2α，B_2ξ分別為：

A_1α＝c₁ω²D²+c₃ωD+c₅I+c₆(ωD+∈₁I)^-1+c₇(ωD+∈₂I)^-1

B_1ξ＝c₀ω²D²+c₂ωD+(c₄+c₁₀)I+c₈(ωD+∈₁I)^-1+c₉(ωD+∈₂I)^-1

A_2α＝d₁ω²D²+d₃ωD+d₅I+d₆(ωD+∈₁I)^-1+d₇(ωD+∈₂I)^-1

B_2ξ＝d₀ω²D²+d₂ωD+d₄I+d₈(ωD+∈₁I)^-1+d₉(ωD+∈₂I)^-1.

式(11)為以時域變量為變量的緊湊型時間離散法代數方程組，使用時-頻轉換關系式和將上式轉換為以頻率變量為變量的緊湊型時間離散法代數方程組(12)：

式(12)含有2N+2個未知數，其中，A₂＝A_2α，A₁＝A_1α，B₂＝B_2ξ，B₁＝B_1ξ。

進一步地，步驟4)中使用標量同倫算法求解上述緊湊型時間離散法代數方程組。

與現有技術相比，本發明具有以下有益的技術效果：

本發明方法基于時間離散法，通過在時間域的離散獲得飛行器機翼氣彈系統的代數方程，避免了一般的非線性系統分析方法中大量的符號運算，同時簡化了系統方程，使得求解效率得到較大提高，通過將時間離散方案與參數掃描法配合，成功避免了一般分析方法中可能出現的非物理解，提高了機翼振動仿真的可靠性，能夠對機翼系統的穩態周期響應進行直接估計，而無需對瞬態振動進行模擬，針對性更強，節省了計算資源，同時也便于分析系統在變參數下動力學響應的變化情況。

附圖說明

圖1為本發明方法的流程圖；

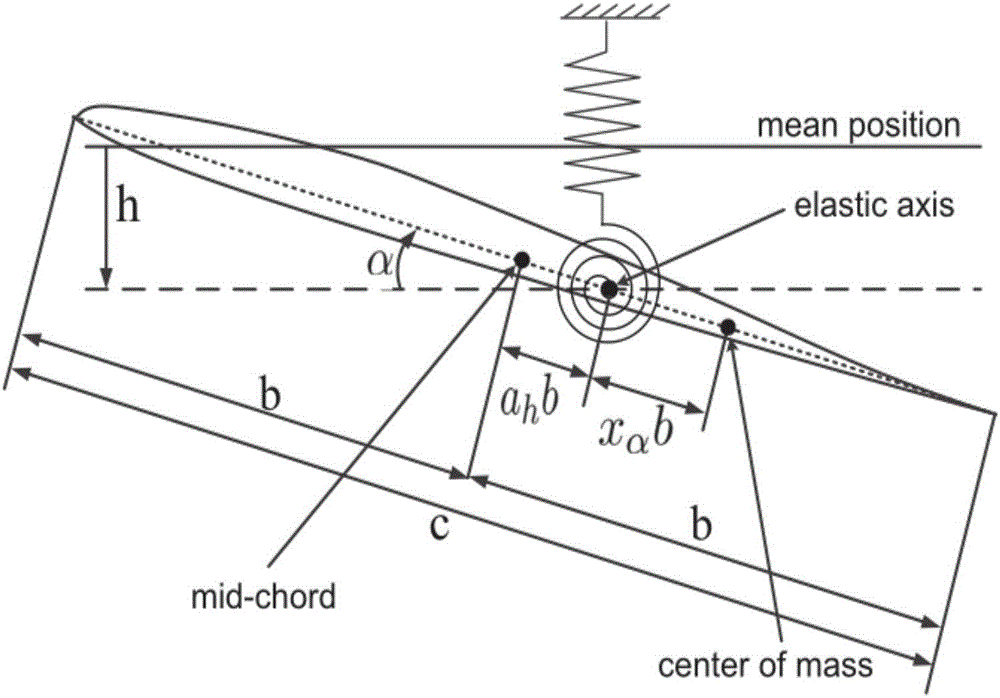
圖2為二元機翼模型示意圖；

圖3為使用低階時間離散法計算的機翼振動頻率和飛行速度響應曲線，其中a)為使用9階時域配點法得到的結果，b)為使用11階時域配點法得到的結果；

圖4為使用高階時間離散法計算的機翼振動頻率和飛行速度響應曲線，其中a)為使用15階時域配點法得到的結果，b)為使用21階時域配點法得到的結果。

具體實施方式

下面對本發明作進一步詳細描述：

一種基于時間離散方法的空天飛行器機翼振動響應的快速仿真方法，該方法的特點在于,采用積分變換方法,將空天飛行器機翼翼型顫振積分-微分方程轉化為純微分方程。進一步，選取含有未知系數的傅里葉級數作為顫振響應近似解，將該近似解帶入顫振微分方程，然后使用時間離散方法將微分方程離散為以傅里葉系數和振動頻率作為待求變量的代數方程組。最后，使用標量同倫法求解待求系數，從而確定空天飛行器機翼顫振的周期解。該方法給出的解釋顫振系統的半解析周期解，該方法具有很高的計算效率和精度。

具體包括以下步驟：

1)空天飛行器機翼顫振動力學模型建立：根據拉格朗日方程，考慮結構非線性和活塞理論，建立空天飛行器在流固耦合下的二元機翼振動原始積分微分方程，并進行無量綱處理。引入一組積分變換式，將積分微分方程中的積分項消除，從而得純微分方程形式的動力學模型。

2)使用時間離散法對機翼顫振動力學方程進行離散化處理：將機翼模型中的待求函數，即機翼俯仰角和沉浮位移，以及由積分變換式引入的變量假設為傅里葉級數的形式，并將傅里葉級數的待求系數組裝成向量。將假設的近似解代入上述微分方程組中，得到殘差函數。然后，迫使殘差函數在一個周期上有限個點上為零得到時間離散法的代數方程組。

3)建立緊湊型的時間離散法代數方程組：由于步驟2中建立的方程組維數太大，不利于計算，因此對其進行等價轉換，以得到緊湊形式的代數方程。利用假設函數為傅里葉級數這一特點，建立離散點與諧波系數之間的矩陣關系，然后通過矩陣變換，建立時間一階導數和二階導數的離散點與諧波系數之間的關系。基于矩陣變換關系，對殘差函數構成的非線性方程組進行逐項處理，并將所得方程組中的線性部分帶入到非線性部分中，就能夠得到形式簡單，維數較低的緊湊型時間離散法代數方程組。

4)使用標量同倫方法求解上述緊湊型的時間離散法代數方程組：時間離散法對初值非常敏感，隨意給定初值一般無法得到真實解，因此，用初值不敏感的標量同倫法為提供合理初值獲得半解析周期解。

為了更好地說明本發明的目的和優點，下面結合附圖和實例對本發明內容做進一步說明：

1.建立二元機翼振動模型的數學模型：

圖2是含有俯仰和沉浮兩自由度的二元機翼振動模型。沉浮用h表示，向下為正方向。關于彈性軸的俯仰用α表示，往上仰為正。彈性軸距翼型中心的距離為a_hb，質心離彈性軸的距離為x_ab；兩個距離的正方向指向機翼后緣。

考慮俯仰和沉浮的結構非線性的無量綱形式系統方程為:

其中x_α是機翼氣彈坐標系原點到質心的無量綱距離，ξ＝h/b是無量綱沉浮量，(·)表示對無量綱時間τ的導數，其中τ＝Ut/b，t為時間，U^*為無量綱速度，定義為U^*＝U/(bω_α)，U為空氣來流速度。其中ω_ξ和ω_α分別是不耦合方程沉浮和俯仰自由度的固有頻率。ζ_ξ和ζ_α是阻尼比，r_α為繞彈性軸的轉矩，α是俯仰角，h是偏轉角，μ＝m/πρb²，m是機翼質量，ρ為空氣密度，b為機翼的半弦長。M(α)和G(ξ)分別是俯仰和沉浮自由度的非線性項，他們的具體表達式為：

M(α)＝α+βα³，G(ξ)＝ξ+γξ³， (3)

其中β和γ為非線性項系數。C_L(τ)和C_M(τ)是線性氣動力和氣動力矩：

其中Wagner函數φ(τ)為ψ₁，ψ₂，ε₁，ε₂是Wagner常數，a_h是機翼中軸線到氣彈坐標原點的無量綱距離。為了便于模型求解，我們引入下面四個積分變換關系式，原方程組可等價變換為如下形式：

其中：

c₀＝1+1/μ，c₁＝x_α-a_h/μ，

c₃＝[1+(1-2a_h)(1-ψ₁-ψ₂)]/μ，c₄＝2(ε₁ψ₁+ε₂ψ₂)/μ，

c₅＝2[1-ψ₁-ψ₂+(1/2-a_h)(ε₁ψ₁+ε₂ψ₂)]/μ，

c₆＝2ε₁ψ₁[1-ε₁(1/2-a_h)]/μ，c₇＝2ε₂ψ₂[1-ε₂(1/2-a_h)]/μ，

其中，r_α為彈性坐標系的回轉半徑。

2.二元機翼模型的時間離散法求解方案：

將方程組(4)中的6個待求函數α(τ)，ξ(τ)，ω_i(τ)，i＝1,2,3,4首先假設成Fourier級數形式。

將假設的近似解(5)代入數學方程(4)中，得到殘差函數：

其中R_j表示現在，迫使殘差函數R_j在一個周期上的2N+1個等距時間點τ_i上為零就可以得到時間離散法代數方程組，該系統含有6×(2N+1)個方程6×(2N+1)+1個未知數。

3.建立緊湊型的時間離散法代數方程組：

對時間離散法代數方程組的每項進行時間離散處理。對α(τ)在2N+1個時間點τ_i離散，可得：

其中θ_i＝ωτ_i，上式可寫為矩陣形式：

也可簡單表示為，

其中

Q_α＝[α₀,α₁,...,α_2N]^T

類似的有其中Q_ξ分別為與ξ有關的配點和諧波系數，和分別為與ω_i有關的配點和諧波系數。

然后，對在2N+1個時間點進行離散可得：

上式易寫為矩陣形式：

令矩陣

因此有：

其中

相同的道理，其中和分別是關于ξ和ω_j導數的配點。

然后，對在2N+1個時間點離散，有：

方程(9)的矩陣形式為：

上式中的方陣可用FA2表示為

因此，

類似的其中和分別是關于ξ和ω_j二階導數的配點。

上面，我們對方程進行了逐項處理，得到了時間離散后的矩陣形式。時間離散法代數方程經變換后得到如下形式：

其中D＝FAF^-1，且

由于只有第二個方程是非線性的，其他五個方程均為線性方程，因此方程組(10)可進一步簡化。將和用表示，然后將他們代入到非線性方程中得：

其中A_1α，B_1ξ，A_2α，B_2ξ為：

A_1α＝c₁ω²D²+c₃ωD+c₅I+c₆(ωD+∈₁I)^-1+c₇(ωD+∈₂I)^-1

B_1ξ＝c₀ω²D²+c₂ωD+(c₄+c₁₀)I+c₈(ωD+∈₁I)^-1+c₉(ωD+∈₂I)^-1

A_2α＝d₁ω²D²+d₃ωD+d₅I+d₆(ωD+∈₁I)^-1+d₇(ωD+∈₂I)^-1

B_2ξ＝d₀ω²D²+d₂ωD+d₄I+d₈(ωD+∈₁I)^-1+d₉(ωD+∈₂I)^-1.

系統(11)為以時域變量為變量的緊湊型時間離散法代數方程組。

使用時-頻轉換關系式和系統(11)變換為：

方程(12)是以頻率變量為變量的緊湊型時間離散法代數方程組，含有2N+2個未知數，其中，A₂＝A_2α，A₁＝A_1α，B₂＝B_2ξ，B₁＝B_1ξ。

4.使用標量同倫方法求解上述緊湊型的時間離散法代數方程組，并結合參數掃描法求解上述緊湊型的時間離散法代數方程組：

時間離散法對初值非常敏感，隨意給定初值一般無法得到真實解，因此，用初值不敏感的標量同倫法為提供合理初值獲得半解析周期解。為了進行系統參數設計，需要求取響應的幅頻曲線。這里使用參數掃描法為時間離散法提供合理初值以獲得幅頻響應曲線。圖3和圖4是時間離散法和RK4計算得出的關于振動基頻比飛行速度的響應曲線。圖3(a)顯示，對于正向掃描，在之前，TDC9和RK4的結果吻合，超過以后TDC9開始與RK4分開。并且，TDC9的響應曲線是連續變化的，也就是說TDC9不能預測出二元機翼振動系統的次級分岔。對于逆向掃描，可以看出TDC9與RK4在整個下支曲線一致。使用RK4預測的分岔點為1.84，超過該分岔點后RK4的響應曲線從下支跳躍到上支。對于TDC9來說，在分岔點之前TDC9能夠得到整個下支響應曲線。但是超越分岔點后，TDC9響應曲線沒有跳躍到上支響應曲線，而是蜿蜒曲折的在下支附近得到其他一些曲線。這是因為到達分岔點后參數掃描法無法提供合理的初值了，掃描法失效。由于TDC法對初值的極其敏感性，因此TDC9在分岔點后的結果對應于非物理解。

圖3(b)是TDC11計算出的頻率--速度響應曲線圖。正向掃描時，TDC11的結果和標準解直到2.27都是很接近的，這要好于TDC9的結果。繼續增大速度TDC11的結果出現偏離，這意味著非物理解出現了。TDC11跟TDC9一樣，都不能檢測出次級分岔點。逆向掃描時，TDC11可以得到整個響應曲線的下支，并且得到了次級Hopf分岔值比標準值1.84略小。由于分岔點使掃描法失效，因此超過分岔點后TDC11給出的是非物理解。

圖4(a)表明逆向掃描時TDC15可以精確的描繪出整個下支響應曲線，但是正向掃描時不能給出整個上支。TDC21的結果見圖4(b)。如圖所示，正向掃描得到了整個上支曲線，并且預測的分岔點為2.38接近標準值2.34。超越分岔點后，不可避免的出現了非物理解。逆向掃描的結果與標準解吻合甚好，整個下支曲線高度一致，分岔點也精確的獲得。超越分岔點后，非物理解分支出現，直到才從非物理解分支跳躍到有物理意義的上支曲線。

總之，使用時間離散法與參數掃描法相結合的辦法可以得到非線性動力學系統的各種響應曲線。并且，隨著諧波個數的增加，計算精度越高。