基于CFD仿真的分叉血管壓力差及FFR的快速計算方法及系統與流程

本發明應用于醫療領域，尤其涉及應用在基于影像修正計算機流體力學(CFD)仿真得到的血管壓力差及FFR的快速計算方法及系統。

背景技術：

常規心血管成像技術如冠狀動脈X射線造影、冠狀動脈CT造影，以及腔內成像技術等，可對冠狀動脈解剖進行成像，顯示血管的損傷部位與損傷范圍，但對于確定損傷是否造成缺血以及定位犯罪血管存在一定的局限性。血流儲備分數FFR可以彌補上述影像技術的不足，優化缺血性心臟病的診斷與犯罪血管的選擇，減少不必要的支架植入，且提高患者的長期治療療效，已成為臨床上評價缺血性心臟病的金標準。

FFR可以由心外膜冠狀動脈狹窄存在的情況下最大心肌血流量除以血管正常時的最大血流量得到。在最大充血情況下，血流量的比值可以用壓力值來代替，因此，利用一個對壓力敏感的冠脈導管，在最大充血情況下，FFR可以通過冠脈遠端狹窄處的壓力(Pd)和血液動力學壓力傳感器得到的大動脈壓力(Pa)相比計算得到。壓力導絲引導的FFR是冠脈狹窄的血液動力學重要指標，但是存在一些局限性，比如有些病人在注入腺苷時反應不適，且壓力導絲造價太高。在現有技術中，在如公開號為CN102905614A的專利文獻，則采用了介入式的方式，通過采集壓力及速度，以積分方式計算FFR值；又如公開號為CN 103829933A的專利文獻中，通過將兩個壓力傳感(壓力傳感器1和壓力傳感器2)介入人體血管中，分別測量兩個壓力傳感器的數值，根據這兩個壓力傳感器測量數值的壓力差，來判斷這兩個壓力傳感器之間是否出現血管狹窄，并通過閾值設置，將測量結果報送醫生診斷；在又如公開號為WO2010033971A1的專利文獻中，同樣采用了植入傳感器的方式，計算FFR值。上述方式均通過介入式獲取FFR值，適用范圍有限，且給病人帶來了較大的痛苦。

而在通過幾何參數等方式的現有技術中，例如公開號為US20150268039A1的專利文獻，通過設置不同位置處的直徑等幾何參數的方式，來計算某段血管近端和遠端的FFR。此外，涂圣賢等人提出了一種新的計算血流儲備分數(FFR)的計算機模型。首先利用三維定量冠脈造影(QCA)得到血管的幾何模型，利用三維QCA和TIMI數幀法得到充血狀態下的平均血流量，把充血狀態下的平均血流量和導管測得的平均血流壓力當做計算流體力學仿真的入口邊界條件，求解流體力學方程得到FFR的計算值。另外，Taylor等人將計算機流體力學應用于計算機斷層掃描冠狀動脈造影(CTA)，得到計算FFR的非侵入式方法。利用CTA得到的冠脈解剖數據，包括血管供應心肌的體積與質量等，估計出最大冠脈血流量，模擬出血管下游微循環阻力，作為計算流體力學仿真的邊界條件進行流體方程求解，獲得FFR的計算值。

上述現有的技術盡管從不同角度、不同計算方法中給出了確定血管壓降的方法，但其仍具有至少以下一種或多個技術缺陷：(1)采用壓力導絲介入血管采集血管的有關幾何參數，成本高昂，且給病人帶來身體損害；(2)采用單一尺度計算方法，盡管可以獲得常規血管狹窄情況下的壓降情況，但卻無法正確區分評估不同程度(如局限性和彌漫性病變并存的血管)狹窄下幾何參數改變對血流壓力的不同影響。(3)根據冠脈造影或CT重建的幾何模型進行計算機流體力學(CFD)仿真，計算復雜度高，計算量大，耗時長。(4)依賴于人為評估病變的尺寸，如病變長度，具有很大的主觀性和誤差，尤其是彌漫性病變。(5)需要利用腺苷誘導冠脈最大充血來計算充血血流速度，操作復雜且加大病人的痛苦。(6)需要對病變血管的分支都進行三維重建，工作量大；(7)在血管具有分叉的情況下，由于參考管腔面積的變化，不能準確計算FFR。

因此需要提供一種準確的血管壓降快速計算方法，其能夠克服上述部分或全部技術缺陷，快速準確地計算FFR數值。在血管重建過程中，對于評估分叉狹窄嚴重性是一個經常遇到的問題，主要是難以確定分叉中心的血管參考管腔，從而影響了從近端主血管到遠端血管的狹窄的綜合分析。涂圣賢等人提出了建立一種新的模型，利用大量彎曲橢圓平面來測量分叉中心，從而解決了確定分叉中心狹窄嚴重性的不明確問題，但是精確度仍然受到限制。一般在CFD仿真重建血管時需要考慮到所有分叉的情況，從而需要很繁重的工作量，難以達到快速計算FFR的作用，如果在CFD仿真時只考慮單支主血管的情況，忽略其他小分叉，計算得到的壓力會不準確，從而影響到FFR的準確性。因此，需要通過單支穩態CFD仿真快速計算壓力分布，利用參考管腔直徑對壓力分布進行校正，準確計算含有分叉的血管的血流儲備分數。

技術實現要素：

有鑒于此，在本發明的一個實施例中，提供了一種基于CFD仿真的分叉血管壓力差的快速計算方法，包括：

接收一段有分叉血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；優選的，所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后血管解剖結構，該血管解剖結構為管腔面積或直徑；

接收該分叉血管段近端終點處的入口血流量及血流壓力；

基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管第一位置處的參考管腔直徑；所述第一位置的位置數據是第一位置到血管近端終點之間的距離；

基于所述幾何模型和近端終點處入口血流量及血流壓力，利用計算流體力學(CFD)仿真得到所述幾何模型上的壓力分布；

基于所述第一幾何參數和第三幾何參數，利用壓力校正公式對上述壓力分布進行校正，計算獲得所述血管近端終點處的第一血流壓力和第一位置處的第二血流壓力之間的壓力差數值ΔP。

優選的，所述方法進一步還包括：以近端終點為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對上述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，...，遠端終點為第n平面，所述n為大于1的自然數值。

優選的，所述方法進一步還包括：所述CFD仿真是穩態血流仿真，設置入口邊界條件為近端終點處入口血流量及血流壓力，出口邊界條件為充分發展的流動；基于所述CFD穩態仿真，計算主支血管第i個平面上的平血血流壓力值P_i。

優選的，所述方法進一步還包括：以近端終點為參考點，根據第一幾何參數、第二幾何參數，以及血管段上某點到參考點的距離x，計算出參考管腔直徑函數；所述參考管腔直徑函數用于代表該段血管不同位置上的參考管腔直徑隨著該位置到參考點的距離x變化的函數；

優選的，計算參考管腔直徑函數包括對血管段的從血管段近端終點到遠端終點范圍內的位置參數進行線性歸一化處理。

優選的，所述方法進一步還包括：基于上述參考管腔直徑函數，計算第i個平面處主支的參考管腔直徑，記作D_i。其中i＝0,1,...,n。

優選的，所述方法進一步還包括：根據第i個平面的參考管腔直徑D_i、平均血流壓力值P_i，血管段近端橫截面的直徑D₀以及近端終點處入口血流壓力P₀，對第i個平面的平均血流壓力P_i進行校正，得到校正后第i個平面的壓力值P_i'；所述壓力校正公式為：

i＝1,2,...,n。

優選的，所述方法進一步還包括：利用所述校正后的壓力值P_i'，可計算獲得第i平面位置的血流壓力和和近端終點處入口血流壓力P₀的壓力差。

同時，本發明還提供了一種基于CFD仿真的分叉血管FFR的快速計算方法，包括：

接收一段有分叉血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；優選的，所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的結果；

接收該分叉血管段近端終點處的入口充血血流量及血流壓力；所述入口充血血流量是該分叉血管在最大充血狀態下的血流量；

基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管第一位置處的參考管腔直徑；所述第一位置的位置數據是第一位置到血管近端終點之間的距離；

基于所述幾何模型和近端終點處入口充血血流量及血流壓力，利用穩態計算流體力學(CFD)仿真得到所述幾何模型上的壓力分布；

基于所述第一幾何參數和第三幾何參數，利用壓力校正公式對上述壓力分布進行校正，計算獲得所述血管近端終點處的第一血流壓力和第一位置處的第二血流壓力之間的比值，即為血流儲備分數。

另外，本發明還提供了一種基于CFD仿真的分叉血管壓力差的快速計算系統，該系統包括：

幾何數據獲取模塊，用于獲得血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；優選的，所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的血管解剖結構，該血管解剖結構為管腔面積或直徑；

參考管腔直徑計算模塊，基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管第一位置處的參考管腔直徑；

主支血管段平面劃分模塊，以近端終點為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對上述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，...，遠端終點為第n平面，所述n為大于1的自然數值。

CFD壓力仿真模塊，基于所述幾何模型和近端終點處入口血流量及血流壓力，利用穩態CFD仿真得到所述幾何模型上的壓力分布，即主支血管段上每一個平面的平均血流壓力；

壓力校正模塊，基于參考管腔直徑利用壓力校正公式對上述壓力分布進行校正，并計算出所述血管近端終點處的第一血流壓力和第i平面處的第二血流壓力之間的壓力差數值ΔP_i。

優選的，所述參考管腔直徑計算模塊，以近端終點為參考點，根據第一幾何參數、第二幾何參數，以及血管段上某點到參考點的距離x，計算出參考管腔直徑函數；所述參考管腔直徑函數用于代表該段血管不同位置上的參考管腔直徑隨著該位置到參考點的距離x變化的函數；

優選的，該系統還包括歸一化模塊，用于在計算參考管腔直徑函數過程中，對血管段的從血管段近端終點到遠端終點范圍內的位置參數進行線性歸一化處理。

優選的，所述壓力校正模塊，是根據第i個平面的參考管腔直徑D_i、平均血流壓力值P_i，血管段近端橫截面的直徑D₀以及近端終點處入口血流壓力P₀，對第i個平面的平均血流壓力P_i進行校正，得到校正后第i個平面的壓力值P_i'；所述壓力校正公式為：

i＝1,2,...,n。

另外，本發明還提供了一種基于CFD的分叉血管血流儲備分數FFR快速計算系統，該系統包括：

幾何數據獲取模塊，用于獲得血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；

優選的，所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的血管解剖結構，該血管解剖結構為管腔面積或直徑；

參考管腔直徑計算模塊，基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管的第一位置處的參考管腔直徑；

主支血管段平面劃分模塊，以近端終點為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對上述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，…，遠端終點為第n平面，所述n為大于1的自然數值；

CFD壓力仿真模塊，基于所述幾何模型和近端終點處入口血流量及血流壓力，利用穩態CFD仿真得到所述幾何模型上的壓力分布，即主支血管段上每一個平面的平均血流壓力；

壓力校正模塊，基于參考管腔直徑利用壓力校正公式對上述壓力分布進行校正，并計算出所述血管近端終點處的第一血流壓力和第i平面處的第二血流壓力之間的壓力差數值ΔP_i。

優選地，第i個平面位置與近端終點處的校正壓力差，利用CFD仿真后得到的第i個平面的平均血流壓力和幾何參數獲得，所述公式為

其中，i＝1,2,…,n。P_i'為校正后的第i個平面的平均血流壓力值，D_i為第i個平面的參考管腔直徑，P_i第i個平面的平均血流壓力值，D₀為血管段近端橫截面的直徑，P₀為近端終點入口處入口血流壓力。

優選地，所述CFD壓力仿真模塊，基于所述幾何模型和近端終點處入口血流量及血流壓力，利用穩態CFD仿真得到所述幾何模型上的壓力分布，即主支血管段上每一個平面的平均血流壓力。

優選地，所述第i個平面的血流儲備分數的計算公式為

其中，ΔP_i是第i個平面位置的壓力差，P₀為近端終點入口處入口血流壓力。

當i的值為n時，即遠端終點時，遠端終點處的血流儲備分數的計算公式為

其中，ΔP_n是遠端終點處到近端終點的壓力差，P₀為近端終點入口處入口血流壓力，n為大于1的自然數。

優選地，所述參考管腔直徑計算模塊，以近端終點為參考點，根據第一幾何參數、第二幾何參數，以及血管段上某點到參考點的距離x，計算出參考管腔直徑函數；所述參考管腔直徑函數用于代表該段血管不同位置上的參考管腔直徑隨著該位置到參考點的距離x變化的函數；第一幾何參數代表該血管段近端橫截面的面積或直徑，第二幾何參數代表該血管段遠端橫截面的面積或直徑。

優選地，該系統還包括歸一化模塊，計算參考管腔直徑函數包括對血管段的從血管段近端終點到遠端終點范圍內的位置參數進行線性歸一化處理。通過歸一化后的參數，形成參考管腔直徑與實際管腔直徑之間的函數關系。

與現有技術相比，本技術將利用血管的參考管腔直徑，對CFD仿真的結果進行校正的算法思想融合進了血管血流儲備分數的計算中來，通過單支穩態CFD仿真快速計算壓力分布，利用參考管腔直徑進行壓力校正，準確計算含有分叉的血管的血流儲備分數，很好地解決了在對CFD仿真過程中，帶有血管分支的情況下，對血管主支中某一特定平面的血流儲備分數計算中的快速準確重建問題，大大提高了血管數據重建速度，并且有效校正了在具有血管分支的情況下，CFD仿真的單支血管壓力分布存在誤差的情況，利用參考管腔直徑對壓力分布進行了精確的校正，從而使得血流儲備分數更加接近實際值，對現有的血流儲備分數的計算進行了改進。

附圖說明

為了更清楚地說明本發明實施例或現有技術中的技術方案，下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹，顯而易見地，下面描述中的附圖僅僅是本發明的一些實施例，對于本領域普通技術人員來講，在不付出創造性勞動的前提下，還可以根據這些附圖獲得其它的附圖。

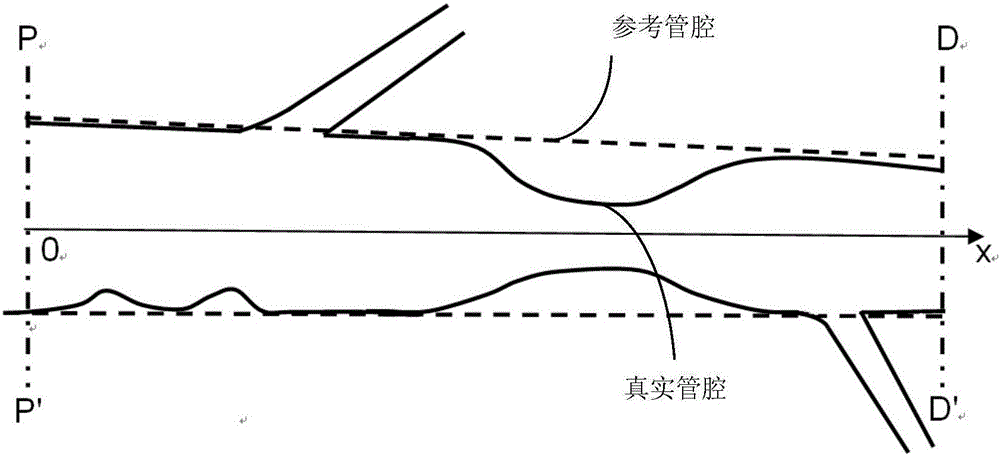
圖1為本發明的實際分叉血管管腔與參考血管管腔結構對比示意圖；

圖2為本發明的沿主支方向血管段平面劃分示意圖；

圖3為本發明的分叉血管壓力差計算系統結構示意圖。

具體實施方式

下面將結合本發明實施例中的附圖，對本發明實施例中的技術方案進行清楚、完整地描述，顯然，所描述的實施例僅僅是本發明一部分實施例，而不是全部的實施例。基于本發明中的實施例，本領域普通技術人員所獲得的所有其他實施例，都屬于本發明保護的范圍。

本領域技術人員應當知曉，下述具體實施例或具體實施方式，是本發明為進一步解釋具體的發明內容而列舉的一系列優化的設置方式，而該些設置方式之間均是可以相互結合或者相互關聯使用的，除非在本發明明確提出了某中某些或某一具體實施例或實施方式無法與其他的實施例或實施方式進行關聯設置或共同使用。同時，下述的具體實施例或者實施方式僅作為最優化的設置方式，而不作為限定本發明的保護范圍的理解。

實施例1：壓力差計算

在本發明的一個具體實施例中，提供了一種基于CFD仿真的分叉血管壓力差的快速計算方法，包括：

接收一段有分叉血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；優選的，所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的血管解剖結構，該血管解剖結構為管腔面積或直徑；

接收該分叉血管段近端終點處的入口血流量及血流壓力；

基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管第一位置處的參考管腔直徑；所述第一位置的位置數據是第一位置到血管近端終點之間的距離；

基于所述幾何模型和近端終點處入口血流量及血流壓力，利用計算流體力學(CFD)仿真得到所述幾何模型上的壓力分布；

基于所述第一幾何參數和第三幾何參數，利用壓力校正公式對上述壓力分布進行校正，計算獲得所述血管近端終點處的第一血流壓力和第一位置處的第二血流壓力之間的壓力差數值ΔP。

參考圖1，示例出本發明中涉及到的血管參考管腔直徑的獲取方式。

在血管基于冠脈影像對分叉血管的主支進行三維重建中，在獲取到管腔的實際直徑的不同點處的參數后，可以通過構建參考管腔直徑函數的方式，模擬出血管的參考管腔直徑變化，從而求得在任意距離處的血管參考管腔直徑，為壓力差的校正及血流儲備分數的計算提供依據。

在一個具體的實施方式中，該參考管腔直徑計算函數可通過如下方式獲得，以近端終點為參考點，根據第一幾何參數、第二幾何參數以及血管段上某點到參考點的距離x，計算出參考管腔直徑函數；所述參考管腔直徑函數用于代表該段血管不同位置上的參考管腔直徑隨著該位置到參考點的距離x變化的函數；

第一幾何參數代表該血管段近端橫截面的面積或直徑，第二幾何參數代表該血管段遠端橫截面的面積或直徑。

優選地，計算參考管腔直徑函數包括對血管段的從血管段近端終點到遠端終點范圍內的位置參數進行線性歸一化處理。通過歸一化后的參數，形成參考管腔直徑與實際管腔直徑之間的函數關系。

參考圖2，對CFD仿真得到所述幾何模型上的壓力分布為例進行說明。

目前，在CFD仿真重建血管時需要考慮到所有分叉的情況，重建出所有的分叉血管，需要很繁重的工作量，難以達到快速計算FFR的作用，如果在CFD仿真時只考慮單支主血管的情況，忽略其他小分叉，計算得到的壓力會不準確，從而影響FFR的準確性。本發明的技術方案，是利用參考管腔直徑對單支穩態CFD仿真得到的壓力分布進行校正，從而能準確計算含有分叉的血管的血流儲備分數。

如圖2所示，考慮一段有分叉的血管，以近端終點所在的平面為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對上述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，…，遠端終點所在的平面是第n平面，所述n為大于1的自然數值。

設置入口邊界條件為近端終點處入口血流量及血流壓力，出口邊界條件為充分發展的流動，基于CFD穩態仿真，計算主支血管第i個平面上的平血血流壓力值Pi。

因為在CFD仿真時，僅考慮了主支血管的情況，而忽略了分叉的情況，從而仿真時高估了主支血管遠端終點的血流量，導致最終得到的血流儲備分數比真實值大，因此需要校正CFD穩態仿真得到的壓力差。

根據參考管腔直徑函數，對第i個平面處與近端終點的壓力差進行校正，可以利用壓力校正公式得到。壓力校正公式為：

其中，i＝1,2,…,n。Pi'為校正后的第i個平面的平均血流壓力值，D_i為第i個平面的參考管腔直徑，P_i第i個平面的平均血流壓力值，D₀為血管段近端橫截面的直徑，P₀為近端終點入口處入口血流壓力。

根據校正后的壓力值，獲得第i個平面位置的血流壓力和近端終點處入口血流壓力的壓力差，因此，第i個平面位置的壓力差ΔP_i的計算公式為

ΔP_i＝P′_i-P₀

其中，P_i'為校正后的第i個平面的平均血流壓力值，P₀為近端終點入口處入口血流壓力。

遠端終點為第n平面，即當i的值為n時，遠端終點處的血流壓力和近端終點入口血流壓力的壓力差為：

ΔP_n＝P′_n-P₀

當計算血流儲備分數時，壓力差應該為根據血管的幾何參數修正后的壓力差，不能直接使用CFD仿真單支血管后的壓力值，否則該壓力值會比真實情況大，導致最終血流儲備分數的計算值比實際值偏小。

由上述例子可見，需要對CFD穩態仿真后得到的壓力分布進行校正，才能得到比較準確的壓力差值，從而得到比較準確的血流儲備分數。

實施例2:FFR計算

在又一個具體的實施例中，本發明還提供了一種基于CFD的血流儲備分數快速計算方法，該方法包括：

接收一段有分叉血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；

接收該分叉血管段近端終點處的入口充血血流量及血流壓力；所述入口充血血流量是該分叉血管在最大充血狀態下的血流量；

基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管第一位置處的參考管腔直徑；所述第一位置的位置數據是第一位置到血管近端終點之間的距離；

基于所述幾何模型和近端終點處入口充血血流量及血流壓力，利用穩態計算流體力學(CFD)仿真得到所述幾何模型上的壓力分布；

基于所述第一幾何參數和第三幾何參數，利用壓力校正公式對上述壓力分布進行校正，計算獲得所述血管近端終點處的第一血流壓力和第一位置處的第二血流壓力之間的比值，即為血流儲備分數。

優選地，所述血管的幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的血管解剖結構，該血管解剖結構為管腔面積或直徑。

優選地，所述CFD仿真是穩態血流仿真，入口邊界條件為近端終點處入口血流量及血流壓力，出口邊界條件是充分發展的流動。

在一個具體的實施方式中，所述的血管的參考直徑的獲取方式可以采用以下方式，以近端終點為參考點，根據第一幾何參數、第二幾何參數，以及血管段上某點到參考點的距離x，計算出參考管腔直徑函數；所述參考管腔直徑函數用于代表該段血管不同位置上的參考管腔直徑隨著該位置到參考點的距離x變化的函數；第一幾何參數代表該血管段近端橫截面的面積或直徑，第二幾何參數代表該血管段遠端橫截面的面積或直徑。

在一個具體的實施方式中，計算參考管腔直徑函數包括對血管段的從血管段近端終點到遠端終點范圍內的位置參數進行線性歸一化處理。通過歸一化后的參數，形成參考管腔直徑與實際管腔直徑之間的函數關系。

在一個具體的實施方式中，主支血管段上每一個平面的平均血流壓力，可以利用穩態CFD仿真得到，所述CFD仿真的入口邊界條件為近端終點處入口血流量及血流壓力，出口邊界條件是充分發展的流動，以近端終點為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對所述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，…，遠端終點為第n平面，所述n為大于1的自然數值。

基于所述CFD仿真，確定主支血管第i個平面上的平血血流壓力值P_i。而在CFD仿真時考慮的是單支血管的情況，需要對血管的壓力分布進行校正。因此，我們根據參考管腔直徑函數，獲得第i個平面處主支的參考管腔直徑D_i，第i個平面處與近端終點的校正壓力差，利用壓力校正公式得到。壓力校正公式為

其中，i＝1,2,…,n。P_i'為校正后的第i個平面的平均血流壓力值，D_i為第i個平面的參考管腔直徑，P_i第i個平面的平均血流壓力值，D₀為血管段近端橫截面的直徑，P₀為近端終點入口處入口血流壓力。

根據校正后的壓力值，獲得第i個平面位置的血流壓力和近端終點處入口血流壓力的壓力差，所述壓力差ΔP_i的計算公式為

ΔP_i＝P′_i-P₀

其中，P_i'為校正后的第i個平面的平均血流壓力值，P₀為近端終點入口處入口血流壓力。

由此可得，第i個平面的血流儲備分數的計算公式為：

其中，ΔP_i是第i個平面位置的壓力差，P₀為近端終點入口處入口血流壓力。

考慮到遠端終點為第n個平面，即當i的值為n時，遠端終點處的血流儲備分數的計算公式為

其中，ΔP_n是遠端終點處到近端終點的壓力差，P₀為近端終點入口處入口血流壓力。

所述血管有n個平面，n是大于1的自然數。

當計算血流儲備分數時，壓力差應該為根據血管的幾何參數修正后的壓力差，不能直接使用CFD仿真單支血管后的壓力值，否則將會造成FFR計算值比實際值偏小。

實施例3：壓力差計算系統

在又一個具體的實施例中，本發明還提供了一種基于CFD的分叉血管壓力差計算系統，該系統可以執行或采用例如實施例1和2中所介紹的具體的方法，結合圖3所示，該系統包括：

幾何數據獲取模塊，用于獲得血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的結果；

參考管腔直徑計算模塊，基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管的第一位置處的參考管腔直徑；

主支血管段平面劃分模塊，以近端終點為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對上述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，…，遠端終點為第n平面，所述n為大于1的自然數值。

CFD壓力仿真模塊，基于所述幾何模型和近端終點處入口血流量及血流壓力，利用穩態CFD仿真得到所述幾何模型上的壓力分布，即主支血管段上每一個平面的平均血流壓力。

壓力校正模塊，基于參考管腔直徑利用壓力校正公式對上述壓力分布進行校正，并計算出所述血管近端終點處的第一血流壓力和第i平面處的第二血流壓力之間的壓力差數值ΔP_i。

在一個具體的實施方式中，所述系統還包含血流儲備分數計算模塊，基于所述近端終點的壓力，以及第i個平面與所述近端終點處的校正壓力差，確定血流儲備分數。

在一個具體的實施方式中，第i個平面位置與近端終點處的校正壓力差，利用CFD仿真后得到的第i個平面的平均血流壓力和幾何參數獲得，所述公式為

其中，i＝1,2,…,n。P_i'為校正后的第i個平面的平均血流壓力值，D_i為第i個平面的參考管腔直徑，P_i第i個平面的平均血流壓力值，D₀為血管段近端橫截面的直徑，P₀為近端終點入口處入口血流壓力。

實施例4：FFR快速計算系統

在又一個具體的實施例中，本發明還提供了一種基于CFD的分叉血管FFR快速計算系統，該系統可以執行或采用例如實施例1和2中所介紹的具體的方法，結合圖3所示，該系統包括：

幾何數據獲取模塊，用于獲得血管的幾何參數和幾何模型，該血管包括近端終點和遠端終點，所述幾何參數包括第一幾何參數，代表該血管段近端橫截面的面積或直徑；第二幾何參數，代表該血管段遠端橫截面的面積或直徑；第三幾何參數，代表該血管段位于近端終點和遠端終點之間的第一位置的橫截面面積或直徑；所述幾何模型是基于冠脈影像對分叉血管的主支進行三維重建后的結果；

參考管腔直徑計算模塊，基于所述第一幾何參數、第二幾何參數、第三幾何參數以及第一位置的位置數據計算該血管的第一位置處的參考管腔直徑；

主支血管段平面劃分模塊，以近端終點為參考平面(記作第0平面)，根據冠脈影像的最大分辨率，對上述幾何模型沿主支方向進行劃分，分別記作第1平面，第2平面，…，遠端終點為第n平面，所述n為大于1的自然數值。

CFD壓力仿真模塊，基于所述幾何模型和近端終點處入口充血血流量及血流壓力，利用穩態CFD仿真得到所述幾何模型上的壓力分布，即主支血管段上每一個平面的平均血流壓力。

壓力校正模塊，基于參考管腔直徑利用壓力校正公式對上述壓力分布進行校正，并計算出所述血管近端終點處的第一血流壓力和第i平面處的第二血流壓力之間的壓力差數值ΔP_i。

在一個具體的實施方式中，所述系統還包含血流儲備分數計算模塊，基于所述近端終點的壓力，以及第i個平面與所述近端終點處的校正壓力差，確定血流儲備分數。

在一個具體的實施方式中，第i個平面位置與近端終點處的校正壓力差，利用CFD仿真后得到的第i個平面的平均血流壓力和幾何參數獲得，所述公式為

其中，i＝1,2,…,n。P_i'為校正后的第i個平面的平均血流壓力值，D_i為第i個平面的參考管腔直徑，P_i第i個平面的平均血流壓力值，D₀為血管段近端橫截面的直徑，P₀為近端終點入口處入口血流壓力。

在一個具體的實施方式中，所述第i個平面的血流儲備分數的計算公式為

其中，ΔP_i是第i個平面位置的壓力差，P₀為近端終點入口處入口血流壓力。

當i的值為n時，即遠端終點時，遠端終點處的血流儲備分數的計算公式為

其中，ΔP_n是遠端終點處到近端終點的壓力差，P₀為近端終點入口處入口血流壓力，n為大于1的自然數。

所述的血管的參考直徑的獲取方式可以采用以下方式，以近端終點為參考點，根據第一幾何參數、第二幾何參數，以及血管段上某點到參考點的距離x，計算出參考管腔直徑函數；所述參考管腔直徑函數用于代表該段血管不同位置上的參考管腔直徑隨著該位置到參考點的距離x變化的函數；第一幾何參數代表該血管段近端橫截面的面積或直徑，第二幾何參數代表該血管段遠端橫截面的面積或直徑。

在一個具體的實施方式中，計算參考管腔直徑函數包括對血管段的從血管段近端終點到遠端終點范圍內的位置參數進行線性歸一化處理。通過歸一化后的參數，形成參考管腔直徑與實際管腔直徑之間的函數關系。