基于靈敏參數驗證與更新的可靠性并行優化設計方法與流程
本發明屬于可靠性優化設計領域,特別涉及一種基于靈敏參數驗證與更新的可靠性并行優化設計方法。
背景技術:
基于可靠性的設計優化(rbdo)是通過考慮材料性質、制造、裝配等方面的不確定性,在設計階段保證可靠性的一種方法。雖然大量高效率且先進的算法如單循環單向量(slsv)、基于安全因子的方法(sfa)和序列優化和可靠性評估(sora)被提出。然而,建模過程中受到各種條件的限制可能導致獲得的信息并不全面,而且所有這些改進算法都是根據準確的模型假設來執行的,因此優化結果的準確性和可靠性存疑,和實際應用還存在一定的距離。
模型驗證與更新技術可以用來表征仿真系統能夠多大程度上代表真實的物理系統。另外,模型驗證與更新不僅僅是一個比較仿真模型與真實系統的過程,也是一個逐漸矯正模型的過程。在rbdo設計中加入模型驗證的思想,可以一邊驗證更新,一邊序列優化設計,利用這種“并行優化”的思想可以優化出期望的真實可靠的結果。
隨著科學技術發展,國內外學者在模型驗證領域提出了大量卓有成效的方法,主要分為:主觀法和客觀法兩大類。主觀法主要依據外在表現或者專家經驗來判斷模型是否有效,不確定性較大,結果往往并不可靠。客觀法一般采用數理統計方法進行驗證,有貝葉斯估計法和極大似然估計法等。貝葉斯估計法一般適用于小樣本問題,而且由于缺乏先驗知識往往對先驗分布很難確定。極大似然估計法可以用來表征模型與實驗之間的極大似然接近,簡單易用。然而,模型驗證技術在面對多參數問題時,其更新效率不容樂觀,靈敏度分析法可以只選出那些影響作用較大的參數用于更新,能夠有效解決效率不高的問題。靈敏度分析法有多種,主要分為局部靈敏度法和全局靈敏度法。前者有直接求導法、有限差分法等。后者有相關系數比率法、基于方差的功能anova法、傅里葉幅值法等,其中功能anova法最為實際,也最為常用。
技術實現要素:
本發明的目的在于克服現有技術的不足,提供一種通過時變靈敏度分析法選取每次迭代過程中少量靈敏度較大的參數作為驗證與更新參數,通過極大似然法對rbdo模型進行驗證更新,實現了多參數模型高效率驗證更新的基于靈敏參數驗證與更新的可靠性并行優化設計方法。
本發明的目的是通過以下技術方案來實現的:基于靈敏參數驗證與更新的可靠性并行優化設計方法,包括以下步驟:
s1、分析產品的誤差關系,建立產品模型與實驗數據之間時變的高斯隨機誤差函數模型,并給定設計變量初始點和閾值;
s2、利用anova法對模型參數進行時變靈敏度分析,對時變靈敏度結果按從大到小的順序排列,選取矩形局部設計子域內靈敏值數量級高于其他參數靈敏度值至少1個數量級的參數作為步驟s3中的驗證與更新參數;
s3、對高斯隨機誤差函數模型進行極大似然估計,然后利用matlab中的fmincon函數對該極大似然函數的倒數進行優化,完成對靈敏參數的驗證與更新;
s4、利用高斯隨機誤差函數模型和fmincon函數仿真出設計變量初始點附近的樣本數據,對樣本數據每一維度數據按大小進行排序,估計出一定置信水平下每一維度上的估計區間,進而組成設計變量初始點整體的矩形局部設計子域;
s5、對設計變量初始點的矩形局部設計子域內的目標函數進行設計優化,得出設計變量優化結果。
s6、判斷設計變量優化結果與設計變量初始點的差值的絕對值是否小于或等于設置的閾值,若是則結束優化,否則將步驟s5得到的設計變量優化結果作為新的設計變量初始點,返回步驟s2;直至設計變量優化結果與設計變量初始點的差值的絕對值小于設置的閾值。
進一步地,步驟s1中時變的高斯誤差函數模型如公式(1)所示:
ytest(x)=ymodel(x,c)+ε(x)(1)
x和c分別表示設計變量和設計參數;ytest(x)表示設計變量x處的試驗響應向量;ymodel(x,c)表示x、c處的模型響應向量;ε(x)表示的是零均值的高斯隨機誤差向量。
進一步地,步驟s2中的時變靈敏度分析方法為:采用所有時刻的慣常靈敏度值在全時域上的平均值來表示,其具體計算如公式(2)所示:
tsi表示第i個因子的時變靈敏度值;m代表區間上時間點個數;si|t表示每一時刻點t處第i個因子的慣常靈敏度值,具體計算如公式(3)所示:
公式(3)中一共有r個輸入因子,
進一步地,步驟s3中的極大似然函數如公式(4)所示:
ε(x)表示零均值高斯隨機誤差,通過公式(1)得到,ε(x)t表示零均值高斯隨機誤差的轉置;γ表示該隨機誤差的協方差,det(γ)表示協方差的行列式;c'表示步驟s2選取的模型參數;n表示試驗數據維度。
進一步地,步驟s4中具體實現方法為:利用高斯隨機誤差函數模型和fmincon函數仿真出設計變量初始點x0附近的樣本數據
矩形局部設計子域估計模型如公式(5)所示:
公式(5)中的極大似然估計相比于公式(4)多了關于設計變量x的輸出,極大似然估計時仿真出一系列關于設計變量x的樣本數據,進而用于矩形局部設計子域的估計。
進一步地,步驟s5中矩形局部設計子域內的優化模型如公式(6)所示:
公式(6)中:f(d,x,p)是局部設計子域內的目標設計函數,根據設計需求得到;d是決定性設計變量;p=(c',c·),c'是步驟s2中選擇的靈敏的參數,c·是不隨矩形局部設計子域改變而改變的參數;pr{·}表示約束的可靠概率值;gk(·)表示可靠性約束;gj(·)表示確定性約束;rk表示可靠性限值;m、n分別表示可靠性約束和總約束的個數。
本發明的有益效果是:本發明針對目前可靠性優化設計中存在的缺陷,提出了一種基于靈敏參數驗證與更新的可靠性并行優化設計方法,該方法通過時變靈敏度分析法選取每次迭代過程中少量靈敏度較大的參數作為驗證與更新參數,通過極大似然法對rbdo模型進行驗證更新,充分考慮了rbdo過程中模型不精確的問題以及利用局部時變靈敏度分析保證驗證更新效率的問題,實現了多參數模型高效率驗證更新,從而保證優化設計模型精確度符合要求,同時為新技術、新材料下新一代產品的可靠性設計優化提供技術支撐,從而縮短了研發周期,具有較高的實用價值和較強的工程意義。
附圖說明
圖1是本發明可靠性并行優化的流程圖。
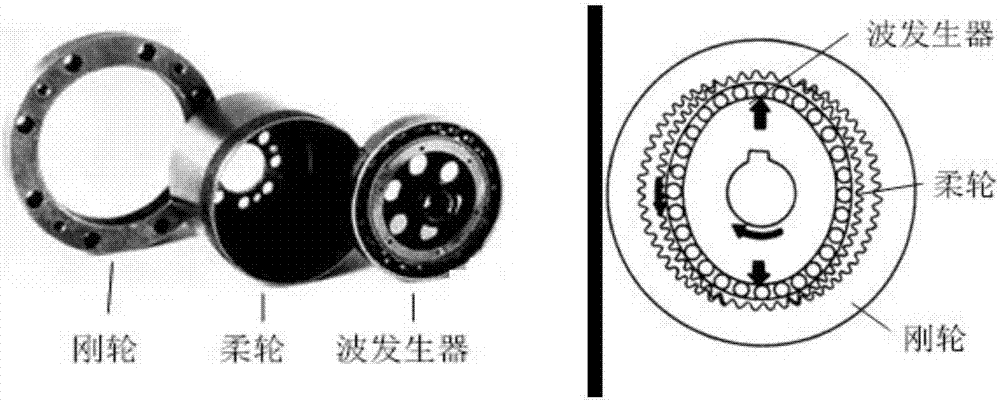
圖2是是具體實例中的諧波減速器示意圖。
圖3是可靠性并行優化設計中的設計變量迭代示意圖。
圖4是可靠性并行優化設計中的模型參數靈敏度值迭代示意圖。
具體實施方式
下面結合附圖進一步說明本發明的技術方案。
如圖1所示,一種基于靈敏參數驗證與更新的可靠性并行優化設計方法,包括以下步驟:
s1、分析產品的誤差關系,建立產品模型與實驗數據之間時變的高斯隨機誤差函數模型,并給定設計變量初始點x0和閾值α;鑒于高斯誤差模型具有較好的普適性,選用高斯誤差函數模型,如公式(1)所示:
ytest(x)=ymodel(x,c)+ε(x)(7)
x和c分別表示設計變量和設計參數;yt(x)表示設計變量x處的試驗響應向量。ym(x,c)表示x、c處的模型響應向量;ε(x)表示的是零均值的高斯隨機誤差向量。該公式以向量形式表征每一時間點處的誤差情況。該公式以向量形式表征每一時間點處的誤差情況。
s2、利用改進的功能anova法對模型參數進行時變靈敏度分析,對時變靈敏度結果按從大到小的順序排列,選取矩形局部設計子域內靈敏值數量級高于其他參數靈敏度值至少1個數量級的參數作為步驟s3中的驗證與更新參數,記為c';時變靈敏度分析方法為:采用所有時刻的慣常靈敏度值在全時域上的平均值來表示,其具體計算如公式(2)所示:
tsi表示第i個因子的時變靈敏度值;m代表區間上時間點個數;si|t表示每一時刻點t處第i個因子的慣常靈敏度值,具體計算如公式(3)所示:
公式(3)中一共有r個輸入因子,
s3、對高斯隨機誤差函數模型進行極大似然估計,然后利用matlab中的fmincon函數對該極大似然函數的倒數進行優化,完成對靈敏參數的驗證與更新;極大似然函數如公式(4)所示:
ε(x)表示零均值高斯隨機誤差,通過公式(1)得到,ε(x)t表示零均值高斯隨機誤差的轉置;γ表示該隨機誤差的協方差,det(γ)表示協方差的行列式;c'表示步驟s2選取的模型參數;n表示試驗數據維度。
s4、利用高斯隨機誤差函數模型和fmincon函數仿真出設計變量初始點附近的樣本數據,對樣本數據每一維度數據按大小進行排序,估計出一定置信水平下每一維度上的估計區間,進而組成設計變量初始點整體的矩形局部設計子域;具體實現方法為:利用高斯隨機誤差函數模型和fmincon函數仿真出設計變量初始點x0附近的樣本數據
矩形局部設計子域估計模型如公式(5)所示:
公式(5)中的極大似然估計相比于公式(4)多了關于設計變量x的輸出,極大似然估計時仿真出一系列關于設計變量x的樣本數據,進而用于矩形局部設計子域的估計。
s5、對設計變量初始點的矩形局部設計子域內的目標函數進行設計優化,得出設計變量優化結果。
s6、判斷設計變量優化結果與設計變量初始點的差值的絕對值是否小于或等于設置的閾值,若是則結束優化,否則將步驟s5得到的設計變量優化結果作為新的設計變量初始點,返回步驟s2;直至設計變量優化結果與設計變量初始點的差值的絕對值小于設置的閾值;矩形局部設計子域內的優化模型如公式(6)所示:
公式(6)中:f(d,x,p)是局部設計子域內的目標設計函數,根據設計需求得到;d是決定性設計變量;p=(c',c●),c'是步驟s2中選擇的靈敏的參數,c●是不隨矩形局部設計子域改變而改變的參數;pr{·}表示約束的可靠概率值;gk(·)表示可靠性約束;gj(·)表示確定性約束;rk表示可靠性限值;m、n分別表示可靠性約束和總約束的個數。優化時在普通尺寸、性能約束中融合不確定因素,形成可靠性約束。
s6、判斷設計變量優化結果與設計變量初始點的差值的絕對值是否小于或等于設置的閾值α,若|x'-x0|≤α則結束優化,否則將步驟s5得到的設計變量優化結果x'作為新的設計變量初始點x0,返回步驟s2;直至設計變量優化結果與設計變量初始點的差值的絕對值小于設置的閾值。
以上步驟中matlab為一款商業數學軟件,fmincon函數為非線性優化函數,兩者均為該領域的慣用軟件和函數,故不再詳細描述,這并不會影響本發明的實施。
下面結合一個具體實例對本發明的方法作進一步說明。本實施例以考慮效率退化的諧波減速器的輕量化設計(體積最小)為實施例,在以本發明方法為前提下進行實施,給出詳細的實施方式和具體地操作過程,但本發明的保護范圍不限于下述的實施案例。
圖2為本實施例所針對的諧波減速器示意圖。具體尺寸關系如圖3所示,圖3(a)表示柔輪主要尺寸,圖3(b)表示軸承主要尺寸。其他的基本參數分別是彈性模量e=2.1*104kg/mm2,軸承內環外徑d1=83mm,柔輪分度圓直徑dr=85.5mm,傳動比i=140,模數m=0.3mm,薄壁軸承外環內徑d=78.4mm,薄壁軸承外環外徑d=83mm,輸出扭矩m2=1000kg.mm,柔輪齒數zr=280。
(1)給定設計變量初值x0=(δ0,b0)=(3.5,13),閾值α=(0.1,0.2)。經仿真計算得到的諧波減速器傳遞效率退化模型如公式(7)、公式(8)所示,其中設計變量x=(δ,b),設計參數
表1設計參數分布情況
那么ymodel(x,c,t)=η(x,c,t)。那么根據參數化抽樣方法通過公式(9)可以得到一些模擬假設的實驗數據。這里高斯噪聲ε(x)在t上每一個時刻的標準差σ=0.25。
ytest(x,t)=η(x,c,t)+ε(x,t)(9)
(2)利用公式(2)進行時變靈敏度計算,得到設計參數的靈敏值:
由結果不難看出,kcf、kh靈敏度值和其余5個參數相差1~2個數量級,對模型相應起到的作用最為顯著,因而第一個設計子域選取kcf、kh為校驗參數。另外,參數靈敏度值會隨著設計子域的迭代而有所不同,因此每一個設計子域選取的校驗參數也可能有所不同。設計子域迭代中設計參數靈敏度值排序情況見表2。
表2設計子域迭代的詳細結果
(3)假設高斯隨機誤差ε(x)各個時間分量相互獨立且同分布,那么它的協方差γ等于σ2乘以單位矩陣en×n。結合模擬的實驗數據,利用公式(4)可以得到校驗參數的極大似然估計值c'=(0.816,0.792)。
(4)設置仿真次數b等于150,利用公式(5)可以進行仿真出設計點x0=(δ0,b0)=(3.5,13)附近大量的樣本數據
(5)考慮諧波柔輪的體積最小化,兼顧減速器運行平穩等限制條件,該實例的可靠性優化模型可以用公式(10)來表征,得到的優化結果為x'≈(2.666,10.886)。
g1(·)表示柔輪不失穩性能函數,其中
g2(·)表示柔輪壁厚性能函數,用來確保柔輪足夠的彎曲剛度。
g3(·)表示柔輪承載能力性能函數,可以防止柔輪過載。
(6)令x0=x',重復步驟s2到步驟s5,直至滿足收斂條件|δk+1-δk|≤0.1或者|bk+1-bk|≤0.2,找到符合條件的最優解。該實例中設計子域迭代的詳細結果見表2,設計變量迭代圖見附圖4,七參數靈敏度值迭代遞減排序見表3,由表3易知6個設計子域內krf、kcf靈敏度值最大,對模型的影響最大,因而表2中一直把它們作為校驗參數。
表3靈敏度值迭代遞減排序
本領域的普通技術人員將會意識到,這里所述的實施例是為了幫助讀者理解本發明的原理,應被理解為本發明的保護范圍并不局限于這樣的特別陳述和實施例。本領域的普通技術人員可以根據本發明公開的這些技術啟示做出各種不脫離本發明實質的其它各種具體變形和組合,這些變形和組合仍然在本發明的保護范圍內。
- 還沒有人留言評論。精彩留言會獲得點贊!