一種用于高質量加工的三角函數加減速控制方法與流程

本發明涉及數控加工技術領域，具體的說是一種用于高質量加工的三角函數加減速控制方法。

背景技術：

數控技術是現代先進制造技術的基礎和核心，在很大程度上反映了一個國家的制造技術水平，是衡量工業現代化的一個重要標志。

實現高速加工和高精加工是數控系統的兩個重要目標。加工的速度直接關系到加工的效率，而加工精度則直接影響到加工質量。隨著現代科學技術與生產的發展，機械加工與測量領域提出了越來越高的速度和精度要求。高速度、高精度、高質量的數控加工對數控系統的計算能力和控制能力提出了更高的要求，主要表現在兩個方面：首先數控系統運算速度要快，而且要求數控機床反應快，即各坐標運動部件能在極短的時間內達到給定的速度，并能在高速運行中快速準確地停止在預定位置，縮短準備時間；另一方面要求加工過程運動平穩，不產生沖擊、失步、超程或振蕩，實現高精度、高質量加工。加減速的控制和規劃是數控系統軌跡規劃的重要組成部分，也是數控系統開發的關鍵技術之一。因此，速度規劃是高速度、高精度、高質量數控加工中的重要環節。

目前，在數控加工領域，常用的速度規劃算法包括直線速度規劃法、S曲線速度規劃法、三次多項式速度規劃法等。傳統的直線加減速控制方法計算量小，控制簡單，但是在加速或減速時存在加速度的突變，很容易導致機床產生振動，影響了加工質量。S曲線速度規劃算法的在一次加速或加速過程中，其速度方程是分段兩段或三段計算的，控制比較復雜，而且其加加速度在在一個加速段或減速段突變四次，在加工復雜零部件時，可能引起刀具的震顫。三次多項式速度規劃算法控制簡單，能實現加速度的連續變化，但是其加加速度仍然是不連續的，在一次加減速過程中，其加加速度突變仍會突變兩次，所以這種方法同樣不利于高質量加工。

技術實現要素：

針對現有技術中存在的上述不足之處，本發明要解決的技術問題是提供一種用于高質量加工的三角函數加減速控制方法。

本發明為實現上述目的所采用的技術方案是：一種用于高質量加工的三角函數加減速控制方法，包括預處理階段和實時插補階段；

所述預處理階段包括以下步驟：用向心化參數方法對待加工的數據點進行歸一化；對待加工的路徑進行快速插補并記錄關鍵信息；

所述快速插補過程中，采用圓弧近似的方法計算進給速度；在每一步插補后記錄已經插補過的路徑的長度；記錄每次加/減速過程的初始和結束的速度及對應的插補參數值；計算出每個加/減速段的最大加速度和最大加加速度、三角函數速度規劃方程，并根據位移方程計算出加/減速段的理論加/減速距離，求出實時插補時加/減速的開始參數；將加減速始末參數、三角函數速度方程系數保存到加減速數組中；

所述實時插補階段包括以下步驟：根據加減速數組中的數據，計算出當前點處的實時速度；采用一階泰勒展開式計算參數初值，用牛頓法迭代后計算出插補參數的精確值，代入參數曲線方程，計算出下一個插補點，從而進行實時插補。

所述向心化參數方法為：

其中，P_k和P_k-1表示待加工路徑的第k+1個和第k個數據點，U_k和U_k-1分別表示數據點P_k和P_k-1對應的歸一化參數，U₀表示第一個數據點P₀對應的歸一化參數，n表示數據點的個數。

所述采用圓弧近似的方法計算進給速度，具體為：

其中，u_i為當前插補點p_i對應的插補參數，T為數控系統的插補周期，ρ_i為插補參數u_i處的曲率半徑，E_c為加工要求的最大弦高誤差，F為數控系統的編程進給速度。

所述已插補過的路徑的長度S_i為預處理插補到插補參數u_i處時走過的路徑，通過下式計算：

其中，S_i-1為插補到插補參數u_i-1時走過的路徑，T為數控系統的插補周期，V(u_i)為插補參數u_i處的進給速度，V(u_t)為插補參數u_t處的進給速度。

所述加/減速段的最大加速度A和最大加加速度J，通過比較|V_e-V_s|和的關系計算：

如果則A＝A_max，J＝J_max；

如果則A＝A_max，

如果則J＝J_max，

其中，A_max為數控系統的最大加速度，J_max為數控系統的最大加加速度，V_s為加/減速段的初始速度，V_e為加/減速段的結束速度。

所述三角函數速度規劃方程加速度段的表達式為：

減速段的表達式為：

其中，A為加/減速段的最大加速度；J為加/減速段的最大加加速度；t為時 間，開始時刻為0；V_a(t)和V_d(t)分別是加速段和減速段的速度；V₀是加/減速段的初始速度。

所述位移方程為對三角函數速度規劃方程求積分后得到的方程，具體為：

加速段的位移S_a(t)表達式為：

減速段的位移S_d(t)表達式為：

其中，A為加/減速段的最大加速度；J為加/減速段的最大加加速度；S₀為初始位移；V₀是加/減速段的初始速度；t為時間，開始時刻為0。

所述理論加/減速距離是指在滿足加工精度要求的條件下，從加/減速的初始速度V_s加/減速到結束速度V_e所需的理論路徑；

理論加速距離s_a的計算公式為：

s_a＝S_a(t_a)-S_a(0)

理論減速距離s_d的計算公式為：

s_d＝S_d(t_d)-S_d(0)

其中，S_a(t_a)為加速段的位移，t_a為加速時間，S_d(t_d)為減速段的位移，t_d為減速時間，且

其中，A為加/減速段的最大加速度；J為加/減速段的最大加加速度。

所述根據加減速數組中的數據，計算出當前點處的實時速度，具體為：假設當前的插補參數為u_i，插補時刻為t_i，當前所處的加/減速段x，則實時速度V_i的計算過程如下：

1)若u_i<AD[x].us，保持刀具做勻速運動，V_i＝V_i-1；

2)若AD[x].us≤u_i<AD[x].ue，則加速段V_i＝V_a(t_i)，減速段V_i＝V_d(t_i)；

3)若u_i-1<AD[x].ue，u_i>AD[x].ue，則x＝x+1，V_i＝V_i-1；

4)若在減速時，u_i<AD[x].ue且V(u_i)≤AD[x].ve，則V_i＝V_i-1；

其中，AD[x]為預處理結束后得到的加減速數組的第x段，AD[x].us、AD[x].ue分別為該加減速段的開始和結束插補參數。

所述一階泰勒展開式為：

其中，C(u)為樣條曲線方程，u為樣條曲線參數，u_i為當前插補參數，V_i為u_i處的速度，u_i+1為下一個插補參數，T為插補周期。

所述的牛頓迭代法的標準迭代公式為：

其中，ξ_k和ξ_k+1是u_i+1分別迭代k次和k+1次后的結果；F(ξ)是構造方程，F'(ξ_k)是其一階導數，F(ξ)的表達式為：

F(ξ)＝||C(ξ)-C(u_i)||-V_iT

其中，C(u_i)為樣條曲線在u_i處的值，C(ξ)為樣條曲線在ξ處的值，ξ代表下一個插補參數u_i+1，V_i為u_i處的速度，T為插補周期。

本發明具有以下優點及有益效果：

1.加工柔性好，平滑程度高。本發明方法的速度曲線為三角函數曲線和線性多項式的結合，加速度和加加速度曲線為三角函數曲線，在每個加/減速階段都可以實現速度、加速度和加加速度的連續變化，從而實現柔性加減速控制。

2.加工精度高。本發明方法在預處理階段采用圓弧近似的方法計算進給速度，考慮了弦高誤差的限制，實時插補時用牛頓迭代法實時計算插補參數，減小了進給速度波動，從而保證了加工精度。

3.執行效率高。預處理階段用于收集要加工的曲線的相關數據并計算速度方程，實時插補階段只需用到預處理階段的數據進行實時樣條插補，運算簡單。

4.通用性強。本發明方法不僅能夠應用于各種樣條曲線插補插補中，而且 可以應用各種插補方法(直線插補、圓弧插補等)中的加減速控制。

附圖說明

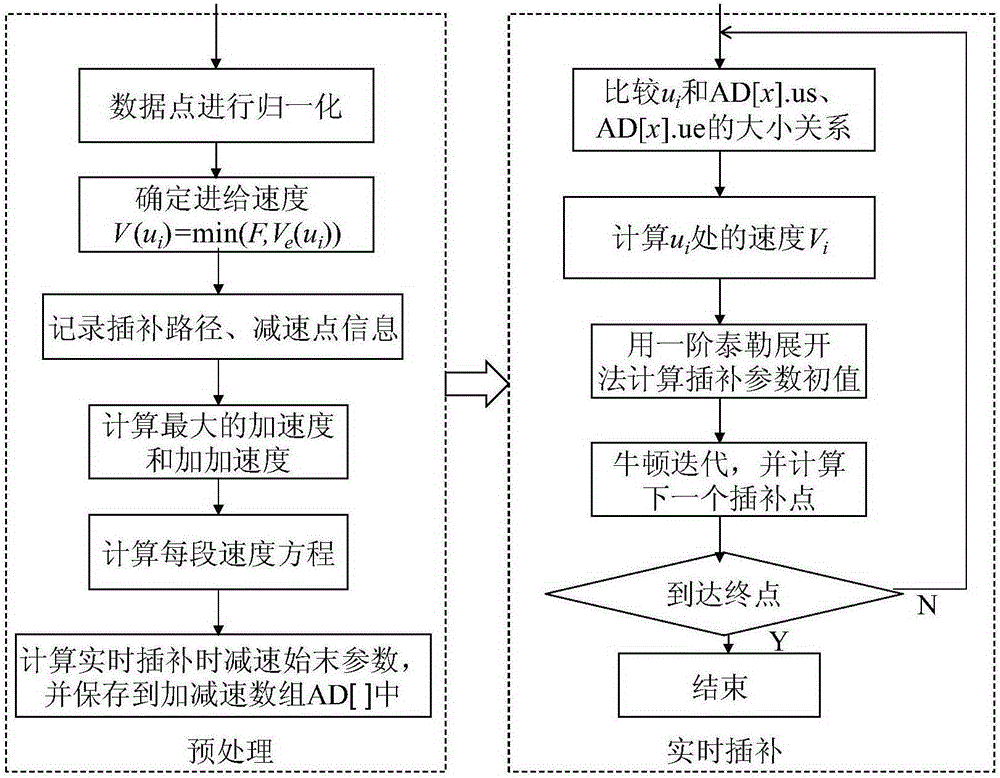
圖1為本發明方法的實施流程圖；

圖2為待加工的樣條曲線；

圖3為利用圓弧近似法計算弦高誤差示意圖；

圖4為本發明方法減速過程的速度、加速度和加加速度曲線；

圖5為采用本發明加工“蝴蝶”NURBS曲線得到的速度曲線；

圖6為采用本發明加工“蝴蝶”NURBS曲線得到的加速度曲線；

圖7為采用本發明加工“蝴蝶”NURBS曲線得到的加加速度曲線；

圖8為采用本發明加工“蝴蝶”NURBS曲線得到的弦高誤差曲線；

圖9為實施例中選擇對比的“蝴蝶”曲線中的矩形區域；

圖10為本發明算法和S曲線、三次多項式速度規劃算法的速度對比曲線；

圖11為本發明算法和S曲線、三次多項式速度規劃算法的加速度對比曲線；

圖12為本發明算法和S曲線、三次多項式速度規劃算法的加加速度對比曲線。

具體實施方式

下面結合附圖及實施例對本發明做進一步的詳細說明。

實施例：將本發明方法在PC上進行仿真驗證，所用的編程軟件為Microsoft Visual Studio 2010，使用C語言編寫程序，這里選用的樣條曲線為NURBS(Non-Uniform Rational B-Spline)曲線。

測試環境的主要技術插補參數如下：

操作系統：Microsoft Windows XP

CPU：Pentium(R)Dual-Core

主頻：2.93GHz

內存：4G

數控系統插補參數如下：

進給率F＝250mm/s；

最大加速度A_max＝5000mm/s²；

最大加加速度J_max＝400000mm/s³；

最大弦高誤差Ec＝0.001mm；

插補周期T＝3ms；

本實施例以典型工件程序“蝴蝶”型曲線的加工為例，如圖2所示。

本發明用于數控加工中樣條插補的速度規劃，其整個插補流程圖如圖1所示。

本發明方法包括預處理和實時樣條插補兩部分。

以減速過程為例，預插補具有以下步驟：

對待加工曲線進行預處理：首先用向心化參數化方法對要加工的數據點進行歸一化，用圓弧近似的方法根據加工精度要求的最大弦高誤差確定進給速度(其示意圖如圖3所示)，并在每次插補后都要記錄插補路徑的長度。此外需要記錄下每次加/減速過程的初始和結束的速度及對應的參數值，然后計算出每個加/減速段的最大加速度和最大加加速度，從而計算出每個加減速段的三角函數速度規劃方程，對其求一階導數和二階導數后，可以分別得到加速度和加加速度的方程(減速過程的速度、加速度和加加速度曲線如圖4所示)。對速度方程求積分后，計算出每個加減速段的位移方程；根據位移方程計算出加/減速段的理論加/加減速距離，最后求出實時插補時加/減速的開始參數。插補過程中，需要將加減速始末參數、三角函數速度方程系數等信息保存到加減速數組中AD[]中。預處理結束后，得到一個加減速段數組AD[n]，n為加/減速度段的個數。

實時插補：根據加減速數組中的數據，計算出當前點處的實時速度，然后采用一階泰勒展開式計算參數初值，用牛頓法迭代后計算出插補參數的精確值，代入參數曲線方程，計算出下一個插補點，從而進行實時插補。

實時樣條插補：首先根據加/減速數組中的速度、初始參數、速度方程信息，計算出在當前參數u_i處的實時進給速度V_i，然后采用一階泰勒展開法實時計算 實時下一個插補參數的迭代初值，然后用牛頓迭代法計算出插補參數的精確值，代入參數方程，計算下一個插補點，進行實時樣條插補。

所述的向心化參數化方法的公式為：

式中，P_k和P_k-1表示要加工路徑的第k+1個和第k個數據點，U_k和U_k-1分別表示P_k和P_k-1對應的歸一化參數，U₀表示第一個數據點P₀對應的參數，n表示數據點的個數，即從0到n-1共n個點。

所述采用圓弧近似的方法計算進給速度V(u_i)的表達式為：

其中，u_i為當前插補點p_i對應的插補參數，T為數控系統的插補周期，ρ_i為參數u_i處的曲率半徑，E_c為加工要求的最大弦高誤差，F為數控系統的編程進給速度。

所述的記錄已插補過的路徑的長度S_i為預處理插補到參數u_i處時走過的路徑，通過以下公式計算：

其中，S_i-1為插補到參數u_i-1時走過的路徑，V(u_i)為參數u_i處的進給速度,V(u_t)為參數u_t處的進給速度。

所述的加速過程的初始速度是指加速開始的速度，假設在參數u_i處加速開始，則加速的初始速度值V(u_i)應該滿足：

V(u_i-1)≤V(u_i)<V(u_i+1)

所述的加速過程的結束速度是指加速結束后的速度，假設在參數u_j處加速開始，則加速的初始速度值V(u_j)應該滿足：

V(u_i-1)<V(u_j)，V(u_j+1)≤V(u_j)

所述的減速過程的初始速度是指減速開始的速度，假設在參數u_x處減速開始，則減速的初始速度值V(u_x)應該滿足：

V(u_x-1)≤V(u_x),V(u_x)>V(u_x+1)

所述的減速過程的結束速度是指減速結束后的速度，假設在參數u_y處減速結束，則減速結束的速度值V(u_y)應該滿足：

V(u_y-1)<V(u_y)≤V(u_y+1)

所述加/減速過程中的最大加速度A和最大加加速度J，通過比較|V_e-V_s|和的關系計算：

如果則A＝A_max，J＝J_max；

如果則A＝A_max，

如果則J＝J_max，

其中A_max為數控系統的最大加速度，J_max為數控系統的最大加加速度V_s是加/減速段的初始速度，V_e加/減速段的結束速度。

所述三角函數速度方程加速度段的表達式為：

減速段的表達式為：

其中，t為時間，開始時刻為0；V_a(t)和V_d(t)分別是加速段和減速段的速度方程；V₀是加速段或減速段的初始速度；A為加減速過程中的最大加速度；J為加減速過程中的最大加加速度。

所述位移方程是指對三角函數速度方程求積分后得到的方程，主要用于計算計算理論加/減速距離，加速段的位移S_a(t)表達式為：

減速段S_d(t)的位移表達式為：

其中，S₀為初始位移，t為時間，開始時刻為0，A為加/減速過程中的最大加速度；J為加/減速過程中的最大加加速度。

所述理論加/減速距離是指在滿足加工精度要求的條件下，從加/減速的初始速度V_s加/減速到結束速度V_e所需的理論路徑。理論加速距離s_a的計算公式為：

s_a＝S_a(t_a)-S_a(0)

理論減速距離s_d的計算公式為：

s_d＝S_d(t_d)-S_d(0)

其中，t_a是加速時間，t_d為減速時間，計算公式為：

式中，A為加/減速過程中的最大加速度；J為加/減速過程中的最大加加速度。

所述實時插補時加/減速的開始參數，是指在進行實時樣條插補時，刀具移動到該插補參數時，開始進行加/減速；以減速過程為例，假設當前從參數為u_i，刀具的速度在參數u_j處達到最小值，減速的開始參數u_d通過以下方法計算：

1)用位移方程計算理論減速距離s_d；

2)向前依次尋找插補參數，找到插補參數u_k，其對應的插補路徑長度S_k滿足：

S_j-S_k≥s_d

3)比較當前插補參數u_i和u_k的大小，若u_i<u_k，則u_d＝u_i，否則u_d＝u_k；

其中，S_j和S_k分別是刀具從0插補到參數u_j和u_k的時走過的路徑。

所述的加減速數組AD[]記錄了預處理中需要保存的加減速段的數據，其形式為：

所述實時插補過程中的實時速度的計算過程為：

假設當前的插補參數為u_i，插補時刻為t_i，當前所處的的加/減速段x，則V_i的計算過程如下：

1)若u_i<AD[x].us，保持刀具做勻速運動，V_i＝V_i-1；

2)若AD[x].us≤u_i<AD[x].ue，則加速段V_i＝V_a(t_i)，減速段V_i＝V_d(t_i)；

3)若u_i-1<AD[x].ue，u_i>AD[x].ue，則x＝x+1，V_i＝V_i-1；

4)若在減速時，u_i<AD[x].ue且V(u_i)≤AD[x].ve，則V_i＝V_i-1；

其中，AD[x]為預處理結束后得到的加減速數組的第x段，AD[x].us、AD[x].ue分別為該加/減速段的開始和結束插補參數。

所述一階泰勒展開法的表達式為：

式中，C(u)為樣條曲線方程，u為樣條曲線參數，u_i為當前插補參數，V_i為u_i處的速度，u_i+1為下一個插補參數，T為插補周期。

所述的牛頓迭代法的標準迭代公式為：

其中，ξ_k和ξ_k+1是u_i+1分別迭代k次和k+1次后的結果；F(ξ)是構造方程，F’(ξ)是其一階導數，F(ξ)的表達式為：

F(ξ)＝||C(ξ)-C(u_i)||-V_iT

式中，C(u)為樣條曲線方程，C(u_i)為樣條曲線在u_i處的值，C(ξ)為樣條曲線 在ξ處的值，ξ代表下一個插補參數u_i+1。

采用本發明算法，對圖2所示的“蝴蝶”曲線進行仿真加工，該樣條曲線公有51個數據點。實驗得到的進給速度曲線、加速度曲線和加加速度曲線分別如圖5～7所示，誤差曲線如圖8所示。為了說明本發明方法的三角函數加減速控制方法的特點，仿真實驗以常用的五段S曲線速度規劃算法、三次多項式速度規劃算法作為對比，對圖2所示的曲線進行了加工，并選擇圖9中的矩形區域作為對比區域，本發明方法與S曲線、三次多項式速度規劃算法的速度、加速度和加加速度曲線對比如圖10～12所示。

通過分析，可以得到如下結論：

1.本發明方法可以滿足加工精度的要求，并保證加工時的進給速度、加速度和加加速度均不超過數控系統的最大限制限制。從圖8可以看出，對蝴蝶型曲線仿真加工后，得到的弦高誤差曲線全部限制在加工精度要求的最大弦高誤差1μm以內；從圖5～7可以看出，本發明算法的進給速度曲線分布在數控系統的編程進給率F內，加速度和加加速度同樣沒有超過系統的最大加速度A_max和加加速度J_max限制，這在一定程度上減小了機床的震動。

2.本發明方法控制比較簡單，執行效率高，且能保證機床運行平穩。預處理階段用于記錄加工曲線的關鍵數據并計算速度方程，而且本發明算法的速度方程是連續定義的。實時插補階段時，只用到預處理階段的數據進行實時樣條插補，操作簡單。從圖5可以看出，刀具在大部分時間內都在做勻速運動，只有在拐角處為了保證加工精度而進行減速控制。這就避免了因頻繁的系統啟動、停止所引起的振動而影響工件程序加工表面光滑度下降的情況。

3.本發明方法可以提高數控系統加工的柔性加減速控制，使機床的運行更加平穩。從圖10～12可以看出，在加減速過程中，本發明算法的速度曲線、加速度曲線和加加速度曲線都是連續變化的，而S曲線速度規劃算法和三次多項式速度規劃的算法的加加速度曲線都是不連續的，一次加速或減速過程中，S曲線算法的加加速度會突變4次，三次多項式算法突變了兩次。由于刀具的加速 度反映了機床的受力情況，而加加速度反映了機床響應速度與運行的平穩性之間的關系。本發明算法的速度方程為三角函數式和線性多項式的結合，加速度方程和加加速度方程為三角函數式，都是連續的，所以本發明算法可以減小因為系統啟動、停止所造成的機床振動，從而提高加工質量。